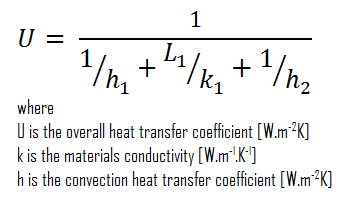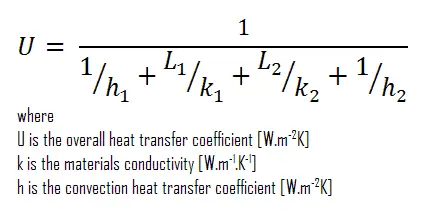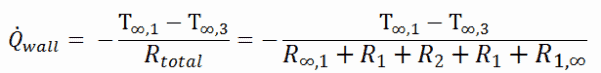Laine de roche – laine de roche
 Laine de roche , également connue sous le nom de laine de roche,est basé sur des minéraux naturels présents en grande quantité sur toute la terre, par exemple des roches volcaniques, typiquement du basalte ou de la dolomie. Outre les matières premières, on peut également ajouter au processus de la laine de roche recyclée ainsi que des résidus de laitier provenant de l’industrie des métaux. Il combine résistance mécanique, bonnes performances thermiques, sécurité incendie et compatibilité avec les températures élevées. La laine de verre et de roche sont produites à partir de fibres minérales et sont donc souvent appelées «laines minérales». La laine minérale est un nom général pour les matériaux fibreux formés par filage ou étirage de minéraux en fusion. La laine de roche est un produit de four de roche en fusion à une température d’environ 1600 ° C, à travers laquelle un courant d’air ou de vapeur est soufflé.
Laine de roche , également connue sous le nom de laine de roche,est basé sur des minéraux naturels présents en grande quantité sur toute la terre, par exemple des roches volcaniques, typiquement du basalte ou de la dolomie. Outre les matières premières, on peut également ajouter au processus de la laine de roche recyclée ainsi que des résidus de laitier provenant de l’industrie des métaux. Il combine résistance mécanique, bonnes performances thermiques, sécurité incendie et compatibilité avec les températures élevées. La laine de verre et de roche sont produites à partir de fibres minérales et sont donc souvent appelées «laines minérales». La laine minérale est un nom général pour les matériaux fibreux formés par filage ou étirage de minéraux en fusion. La laine de roche est un produit de four de roche en fusion à une température d’environ 1600 ° C, à travers laquelle un courant d’air ou de vapeur est soufflé.
Les applications de la laine de roche comprennent l’isolation structurelle des tuyaux, la filtration, l’insonorisation et le milieu de croissance hydroponique. La laine de roche est un matériau polyvalent qui peut être utilisé pour l’isolation des murs, des toits et des sols. Lors de l’installation de la laine de roche, il convient de la maintenir au sec en permanence, car une augmentation de la teneur en humidité entraîne une augmentation significative de la conductivité thermique.
Conductivité thermique de la laine de roche
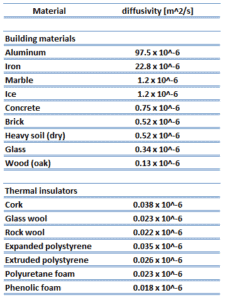 La conductivité thermique est définie comme la quantité de chaleur (en watts) transférée à travers une zone carrée de matériau d’épaisseur donnée (en mètres) en raison d’une différence de température . Plus la conductivité thermique du matériau est faible, plus la capacité du matériau à résister au transfert de chaleur est grande, et donc plus l’efficacité de l’isolation est grande. Les valeurs de conductivité thermique typiques pour les laines minérales sont comprises entre 0,020 et 0.040W / m ∙ K .
La conductivité thermique est définie comme la quantité de chaleur (en watts) transférée à travers une zone carrée de matériau d’épaisseur donnée (en mètres) en raison d’une différence de température . Plus la conductivité thermique du matériau est faible, plus la capacité du matériau à résister au transfert de chaleur est grande, et donc plus l’efficacité de l’isolation est grande. Les valeurs de conductivité thermique typiques pour les laines minérales sont comprises entre 0,020 et 0.040W / m ∙ K .
En général, l’ isolation thermique repose principalement sur la très faible conductivité thermique des gaz . Les gaz possèdent de mauvaises propriétés de conduction thermique par rapport aux liquides et aux solides et constituent donc un bon matériau d’isolation s’ils peuvent être piégés (par exemple dans une structure semblable à de la mousse). L’air et les autres gaz sont généralement de bons isolants. Mais le principal avantage est en l’absence de convection. Par conséquent, de nombreux matériaux isolants (par exemple la laine de roche ) fonctionnent simplement en ayant un grand nombre de poches remplies de gaz qui empêchent la convection à grande échelle .
L’alternance de la poche de gaz et du matériau solide fait que la chaleur doit être transférée à travers de nombreuses interfaces provoquant une diminution rapide du coefficient de transfert de chaleur.
Exemple – Isolation en laine de roche
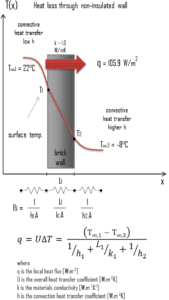 Les murs constituent une source majeure de perte de chaleur dans une maison. Calculez le taux de flux de chaleur à travers un mur de 3 mx 10 m (A = 30 m 2 ). Le mur a une épaisseur de 15 cm (L 1 ) et il est fait de briques avec une conductivité thermique de k 1 = 1,0 W / mK (mauvais isolant thermique). Supposons que les températures intérieure et extérieure sont de 22 ° C et -8 ° C et que les coefficients de transfert de chaleur par convection sur les côtés intérieur et extérieur sont h 1 = 10 W / m 2 K et h 2 = 30 W / m 2K, respectivement. A noter que ces coefficients de convection dépendent fortement notamment des conditions ambiantes et intérieures (vent, humidité, etc.).
Les murs constituent une source majeure de perte de chaleur dans une maison. Calculez le taux de flux de chaleur à travers un mur de 3 mx 10 m (A = 30 m 2 ). Le mur a une épaisseur de 15 cm (L 1 ) et il est fait de briques avec une conductivité thermique de k 1 = 1,0 W / mK (mauvais isolant thermique). Supposons que les températures intérieure et extérieure sont de 22 ° C et -8 ° C et que les coefficients de transfert de chaleur par convection sur les côtés intérieur et extérieur sont h 1 = 10 W / m 2 K et h 2 = 30 W / m 2K, respectivement. A noter que ces coefficients de convection dépendent fortement notamment des conditions ambiantes et intérieures (vent, humidité, etc.).
- Calculez le flux de chaleur ( perte de chaleur ) à travers ce mur non isolé.
- Supposons maintenant une isolation thermique sur le côté extérieur de ce mur. Utilisez une isolation en laine de roche de 10 cm d’épaisseur (L 2 ) avec une conductivité thermique de k 2 = 0,022 W / mK et calculez le flux de chaleur ( perte de chaleur ) à travers ce mur composite.
Solution:
Comme cela a été écrit, de nombreux processus de transfert de chaleur impliquent des systèmes composites et impliquent même une combinaison de conduction et de convection . Avec ces systèmes composites, il est souvent commode de travailler avec un coefficient global de transfert de chaleur , connu comme un facteur U . Le facteur U est défini par une expression analogue à la loi de Newton du refroidissement :
Le coefficient global de transfert de chaleur est lié à la résistance thermique totale et dépend de la géométrie du problème.
- mur nu
En supposant un transfert de chaleur unidimensionnel à travers la paroi plane et sans tenir compte du rayonnement, le coefficient de transfert de chaleur global peut être calculé comme suit:
Le coefficient global de transfert de chaleur est alors:
U = 1 / (1/10 + 0,15 / 1 + 1/30) = 3,53 W / m 2 K
Le flux de chaleur peut alors être calculé simplement comme:
q = 3,53 [W / m 2 K] x 30 [K] = 105,9 W / m 2
La perte de chaleur totale à travers ce mur sera:
q perte = q. A = 105,9 [W / m 2 ] x 30 [m 2 ] = 3177 W
- mur composite avec isolation thermique
En supposant un transfert de chaleur unidimensionnel à travers la paroi composite plane, aucune résistance de contact thermique et sans tenir compte du rayonnement, le coefficient de transfert de chaleur global peut être calculé comme suit:
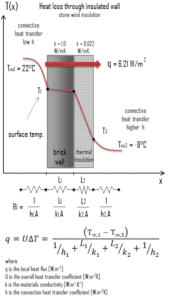 Le coefficient global de transfert de chaleur est alors:
Le coefficient global de transfert de chaleur est alors:
U = 1 / (1/10 + 0,15 / 1 + 0,1 / 0,022 + 1/30) = 0,207 W / m 2 K
Le flux de chaleur peut alors être calculé simplement comme:
q = 0,207 [W / m 2 K] x 30 [K] = 6,21 W / m 2
La perte de chaleur totale à travers ce mur sera:
q perte = q. A = 6,21 [W / m 2 ] x 30 [m 2 ] = 186 W
Comme on peut le voir, un ajout d’isolant thermique entraîne une diminution importante des pertes de chaleur. Il faut l’ajouter, un ajout de la prochaine couche d’isolant thermique ne provoque pas de telles économies. Cela peut être mieux vu de la méthode de résistance thermique, qui peut être utilisée pour calculer le transfert de chaleur à travers les murs composites . Le taux de transfert thermique constant entre deux surfaces est égal à la différence de température divisée par la résistance thermique totale entre ces deux surfaces.