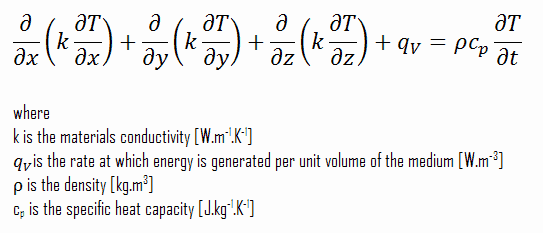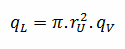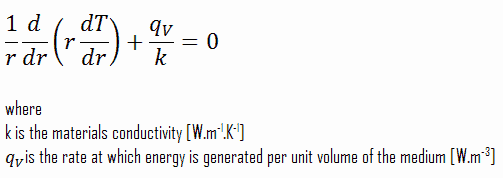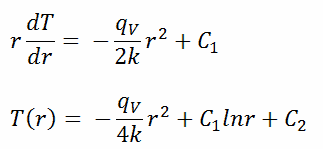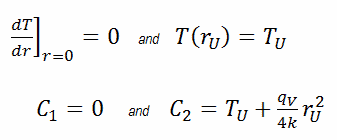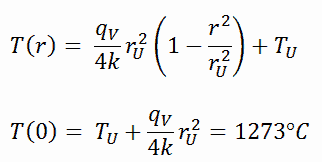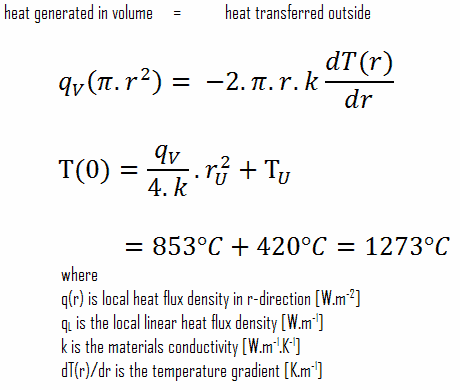Conduction thermique – Conduction thermique
La conduction thermique , également appelée conduction thermique , se produit dans un corps ou entre deux corps en contact sans implication de flux de masse et de mélange. C’est l’échange microscopique direct de l’énergie cinétique des particules à la frontière entre deux systèmes. Le transfert de chaleur par conduction dépend de la «force» motrice de la différence de température et de la conductivité thermique (ou de la résistance au transfert de chaleur). La conductivité thermique dépend de la nature et des dimensions du caloporteur. Tous les problèmes de transfert de chaleur impliquent la différence de température , la géométrieet les propriétés physiques de l’objet étudié. Dans les problèmes de transfert de chaleur en conduction, l’objet étudié est généralement un solide.
Microscopiquement, ce mode de transfert d’énergie est attribué au flux d’électrons libres des niveaux d’énergie supérieurs à inférieurs, aux vibrations du réseau et aux collisions moléculaires . Considérons un bloc de pierre à haute température, constitué d’atomes oscillant intensément autour de leurs positions moyennes. À basse température , les atomes continuent à osciller, mais avec moins d’intensité .
Si un bloc de pierre plus chaud est mis en contact avec un bloc plus froid, les atomes qui oscillent intensément au bord du bloc plus chaud dégagent son énergie cinétique aux atomes les moins oscillants situés au bord du bloc froid. Dans ce cas, il y a transfert d’énergie entre ces deux blocs et la chaleur circule du bloc le plus chaud au bloc le plus froid par ces vibrations aléatoires. La vision moderne consiste à attribuer le transfert d’énergie aux ondes de réseau induites par le mouvement atomique. Dans un isolant électrique, le transfert d’énergie se fait exclusivement via ces ondes de réseau. Dans un conducteur, cela est également dû au mouvement de translation des électrons libres.
Voir aussi: Loi Zéroth de la thermodynamique
En général, les métaux sont généralement de bons conducteurs d’ énergie thermique . Il est étroitement associé à sa bonne conductivité électrique . Pour les métaux, la conductivité thermique est assez élevée et les métaux qui sont les meilleurs conducteurs électriques sont également les meilleurs conducteurs thermiques. Cela est dû à la manière dont les métaux se lient chimiquement. Les liaisons métalliques ont des électrons en mouvement libre ( électrons libres) qui transfèrent rapidement l’énergie thermique à travers le métal. Le fluide électronique d’un solide métallique conducteur conduit la majeure partie du flux de chaleur à travers le solide. Le flux de phonons est toujours présent mais transporte moins d’énergie. Ces mécanismes de conduction thermique seront discutés plus tard.
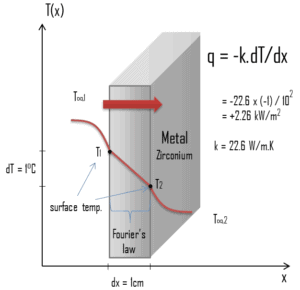
Loi de Fourier sur la conduction thermique
Les processus de transfert de chaleur peuvent être quantifiés en termes d’équations de taux appropriées. L’équation de vitesse dans ce mode de transfert de chaleur est basée sur la loi de Fourier de conduction thermique . Cette loi stipule que le temps de transfert de chaleur à travers un matériau est proportionnel au gradient négatif de la température et à la surface, perpendiculairement à ce gradient, à travers lequel la chaleur circule. Sa forme différentielle est:
La constante de proportionnalité obtenu dans la relation est connue comme la conductivité thermique , k (ou λ ), de la matière. Un matériau qui transfère facilement de l’énergie par conduction est un bon conducteur thermique et a une valeur élevée de k . La loi de Fourier est une expression qui définit la conductivité thermique .
Comme on peut le voir, pour résoudre la loi de Fourier, nous devons impliquer la différence de température, la géométrie et la conductivité thermique de l’objet. Cette loi a été formulée pour la première fois par Joseph Fourier en 1822 qui a conclu que « le flux de chaleur résultant de la conduction thermique est proportionnel à l’amplitude du gradient de température et opposé à celui-ci en signe ».
De même que la loi de Fourier détermine le flux de chaleur à travers une dalle, elle peut également être utilisée pour déterminer la différence de température, lorsque q est connu. Ceci peut être utilisé pour le calcul de la température au centre de la pastille de combustible comme cela sera montré dans les sections suivantes.
Équation de conduction thermique
Dans les sections précédentes, nous avons traité en particulier du transfert de chaleur en régime permanent unidimensionnel, qui peut être caractérisé par la loi de conduction thermique de Fourier . Mais son applicabilité est très limitée. Cette loi suppose un transfert de chaleur en régime permanent à travers un corps plan (notez que la loi de Fourier peut également être dérivée pour les coordonnées cylindriques et sphériques), sans sources de chaleur . C’est simplement l’équation du taux dans ce mode de transfert de chaleur, où le gradient de température est connu.
Mais un problème majeur dans la plupart des analyses de conduction est de déterminer le champ de température dans un milieu résultant des conditions imposées à ses frontières. En ingénierie, nous devons résoudre des problèmes de transfert de chaleur impliquant différentes géométries et différentes conditions telles qu’un élément combustible nucléaire cylindrique, qui implique une source de chaleur interne ou la paroi d’une enceinte sphérique. Ces problèmes sont plus complexes que les analyses planaires que nous avons faites dans les sections précédentes. C’est pourquoi ces problèmes feront l’objet de cette section, dans laquelle l’ équation de conduction thermique sera introduite et résolue.
Voir aussi : Équation de la chaleur
Équation de conduction thermique – Forme générale
L’ équation de conduction thermique est une équation différentielle partielle qui décrit la distribution de la chaleur (ou le champ de température ) dans un corps donné au fil du temps. La connaissance détaillée du champ de température est très importante dans la conduction thermique à travers les matériaux. Une fois cette distribution de température connue, le flux thermique de conduction en tout point du matériau ou à sa surface peut être calculé à partir de la loi de Fourier .
L’équation de la chaleur est dérivée de la loi de Fourier et de la conservation de l’énergie . La loi de Fourier stipule que le taux de temps de transfert de chaleur à travers un matériau est proportionnel au gradient négatif de la température et à la zone, perpendiculairement à ce gradient, à travers laquelle la chaleur circule.
Un changement d’énergie interne par unité de volume dans le matériau, ΔQ, est proportionnel au changement de température, u. C’est-à-dire:
Q = ρ.c p .∆T
Forme générale
En utilisant ces deux équations, nous pouvons dériver l’équation générale de conduction thermique :
Cette équation est également connue sous le nom d’ équation de Fourier-Biot et fournit l’outil de base pour l’analyse de la conduction thermique. A partir de sa solution, on peut obtenir le champ de température en fonction du temps.
En termes simples, l’ équation de conduction thermique indique que :
En tout point du milieu, le taux net de transfert d’énergie par conduction dans un volume unitaire plus le taux volumétrique de production d’énergie thermique doit être égal au taux de variation de l’énergie thermique stockée dans le volume.
Voir aussi : Diffusivité thermique
Exemple – Conduction thermique dans le crayon combustible
La plupart des REP utilisent le combustible à l’ uranium , qui se présente sous forme de dioxyde d’uranium . Le dioxyde d’uranium est un solide semi-conducteur noir à très faible conductivité thermique. D’autre part, le dioxyde d’uranium a un point de fusion très élevé et a un comportement bien connu. L’UO 2 est pressé en pastilles cylindriques , ces pastilles sont ensuite frittées dans le solide.
Ces pastilles cylindriques sont ensuite chargés et encapsulés dans une barre de combustible (ou aiguille de combustible), qui est constitué d’alliages de zirconium en raison de sa très faible absorption section transversale (contrairement à l’acier inoxydable). La surface du tube, qui recouvre les pastilles, est appelée gaine combustible .
Voir aussi : Conduction thermique du dioxyde d’uranium
Le comportement thermique et mécanique des pastilles et des crayons combustibles constitue l’une des trois principales disciplines de conception. Le combustible nucléaire est exploité dans des conditions très inhospitalières (thermiques, radiatives, mécaniques) et doit résister à des conditions de fonctionnement supérieures à la normale. Par exemple, les températures au centre des pastilles de combustible atteignent plus de 1000°C (1832°F) accompagnées de dégagements de gaz de fission. Par conséquent, une connaissance détaillée de la répartition de la température dans un seul crayon de combustible est essentielle pour une exploitation sûre du combustible nucléaire. Dans cette section, nous étudierons l’équation de conduction thermique en coordonnées cylindriquesen utilisant la condition aux limites de Dirichlet avec une température de surface donnée (c’est-à-dire en utilisant la condition aux limites de Dirichlet). Une analyse complète du profil de température des crayons combustibles sera étudiée dans une section distincte.
Température dans l’axe d’une pastille de combustible
Considérons la pastille de combustible de rayon r U = 0,40 cm , dans laquelle il y a une génération de chaleur uniforme et constante par unité de volume, q V [W/m 3 ] . Au lieu du taux de chaleur volumétrique q V [W/m 3 ], les ingénieurs utilisent souvent le taux de chaleur linéaire, q L [W/m] , qui représente le taux de chaleur d’un mètre de crayon combustible. Le taux de chaleur linéaire peut être calculé à partir du taux de chaleur volumétrique par :
La ligne médiane est prise comme origine pour la coordonnée r. En raison de la symétrie dans la direction z et dans la direction azimutale, nous pouvons séparer des variables et simplifier ce problème en un problème unidimensionnel . Ainsi, nous allons résoudre pour la température en fonction du rayon, T(r) , uniquement. Pour une conductivité thermique constante , k, la forme appropriée de l’ équation de la chaleur cylindrique , est :
La solution générale de cette équation est :
où C 1 et C 2 sont les constantes d’intégration.
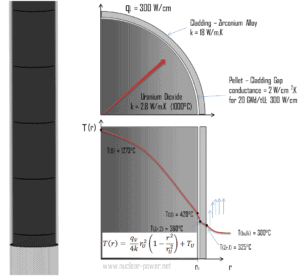
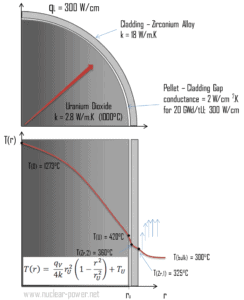Calculer la distribution de température, T(r) , dans cette pastille de combustible, si :
- la température à la surface de la pastille de combustible est T U = 420°C
- le rayon des pastilles de combustible r U = 4 mm .
- la conductivité moyenne du matériau est k = 2,8 W/mK (correspond au dioxyde d’uranium à 1000°C)
- le taux de chaleur linéaire est q L = 300 W/cm et donc le taux de chaleur volumétrique est q V = 597 x 10 6 W/m 3
Dans ce cas, la surface est maintenue à des températures données T U . Ceci correspond à la condition aux limites de Dirichlet . De plus, ce problème est thermiquement symétrique et nous pouvons donc utiliser également la condition aux limites de symétrie thermique . Les constantes peuvent être évaluées par substitution dans la solution générale et sont de la forme :
La distribution de température résultante et la température centrale (r = 0) (maximum) dans cette pastille de combustible cylindrique à ces conditions aux limites spécifiques seront :
Le flux de chaleur radial à n’importe quel rayon, q r [Wm -1 ], dans le cylindre peut, bien sûr, être déterminé en utilisant la distribution de température et avec la loi de Fourier . Notez que, avec la génération de chaleur, le flux de chaleur n’est plus indépendant de r.
∆T dans la pastille de combustible
Une connaissance détaillée de la géométrie, du rayon extérieur de la pastille de combustible, du taux de chaleur volumétrique et de la température de surface de la pastille (T U ) détermine ∆T entre la surface extérieure et l’axe de la pastille de combustible. Par conséquent, nous pouvons calculer la température médiane (T Zr,2 ) simplement en utilisant la conservation d’énergie entre la chaleur générée dans le volume et la chaleur transférée à l’extérieur du volume :
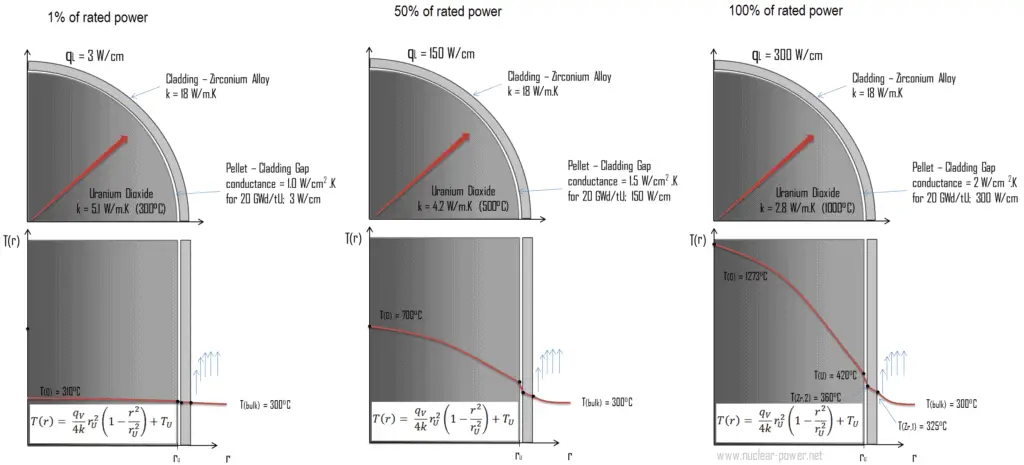
La figure suivante montre la répartition de la température dans la pastille de combustible à différents niveaux de puissance.
______
La température dans un réacteur en fonctionnement varie d’un point à un autre dans le système. En conséquence, il y a toujours un crayon combustible et un volume local , qui sont plus chauds que tous les autres. Afin de limiter ces points chauds, des limites de puissance crête doivent être introduites. Les limites de puissance de pointe sont associées à une crise d’ébullition et aux conditions qui pourraient provoquer la fonte des pastilles de combustible. Cependant, des considérations métallurgiques imposent une limite supérieure à la température de la gaine du combustible et de la pastille de combustible. Au dessus de ces températuresil y a un risque que le carburant soit endommagé. L’un des objectifs majeurs de la conception d’un réacteur nucléaire est d’assurer l’évacuation de la chaleur produite au niveau de puissance souhaité, tout en garantissant que la température maximale du combustible et la température maximale de la gaine soient toujours inférieures à ces valeurs prédéterminées.
