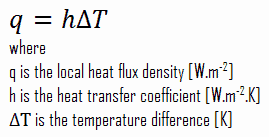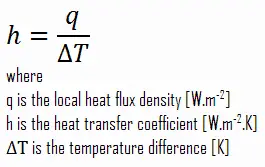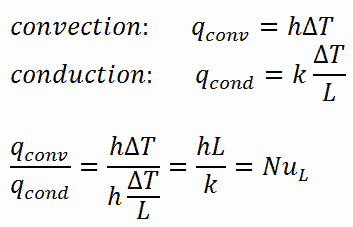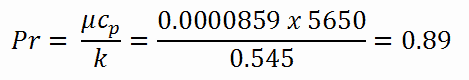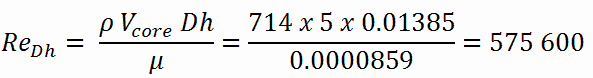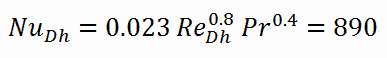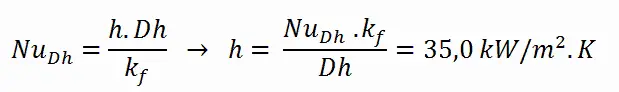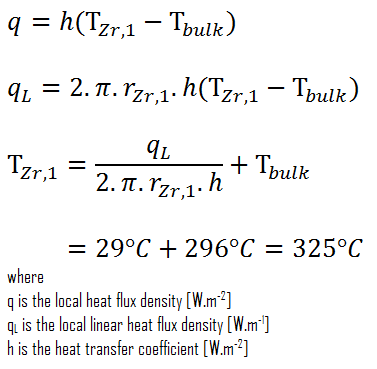Qu’est-ce que la convection – Transfert de chaleur par convection – Définition

Qu’est-ce que la convection

En général, la convection est soit le transfert de masse soit le transfert de chaleur dû au mouvement massif des molécules dans les fluides tels que les gaz et les liquides. Bien que les liquides et les gaz ne soient généralement pas de très bons conducteurs de chaleur, ils peuvent transférer la chaleur assez rapidement par convection .

La convection a lieu par advection , diffusion ou les deux. La convection ne peut pas avoir lieu dans la plupart des solides car ni diffusion importante de la matière ni flux de courant en vrac ne peuvent avoir lieu. La diffusion de la chaleur a lieu dans des solides rigides, mais c’est ce qu’on appelle la conduction thermique .

Le processus de transfert de chaleur entre une surface et un fluide s’écoulant en contact avec elle est appelé transfert de chaleur par convection . En ingénierie, le transfert de chaleur par convection est l’un des principaux mécanismes de transfert de chaleur . Lorsque la chaleur doit être transférée d’un fluide à un autre à travers une barrière, la convection est impliquée des deux côtés de la barrière. Dans la plupart des cas, la principale résistance au flux de chaleur se fait par convection. Le transfert de chaleur par convection a lieu à la fois par diffusion thermique (le mouvement aléatoire des molécules de fluide) et par advection, dans laquelle la matière ou la chaleur est transportée par le mouvement à plus grande échelle des courants dans le fluide.

Mécanisme de convection

En conduction thermique , l’ énergie est transférée sous forme de chaleur soit en raison de la migration d’électrons libres ou d’ ondes vibratoires en treillis ( phonons ). Il n’y a pas de mouvement de masse dans le sens du flux d’énergie. Le transfert de chaleur par conduction dépend de la «force» motrice de la différence de température. La conduction et la convection sont similaires en ce que les deux mécanismes nécessitent la présence d’un milieu matériel (par rapport au rayonnement thermique). En revanche, ils sont différents en ce que la convection nécessite la présence d’un mouvement fluide.

Il faut souligner qu’en surface, le flux d’énergie se produit  uniquement par conduction, même en conduction. Cela est dû au fait qu’il y a toujours une fine couche de film fluide stagnant sur la surface de transfert de chaleur.  Mais dans les couches suivantes, il se produit à la fois un mouvement de conduction et de diffusion-masse au niveau moléculaire ou au niveau macroscopique. En raison du mouvement de masse, le taux de transfert d’énergie est plus élevé. Plus la vitesse de déplacement de la masse est élevée, plus la couche de film fluide stagnante sera mince et plus le débit de chaleur sera élevé.

Il faut noter que l’ ébullition nucléée à la surface perturbe efficacement cette couche stagnante et, par conséquent, l’ébullition nucléée augmente considérablement la capacité d’une surface à transférer l’énergie thermique au fluide en vrac.

Comme il a été écrit, le transfert de chaleur à travers un fluide se fait par convection en présence d’un mouvement de masse et par conduction en son absence. Par conséquent, la conduction thermique dans un fluide peut être considérée comme le cas limite de convection, correspondant au cas du fluide au repos.

La convection comme conduction avec mouvement fluide

Certains experts ne considèrent pas la convection comme un mécanisme fondamental de transfert de chaleur car il s’agit essentiellement de la conduction de chaleur en présence d’un mouvement de fluide. Ils considèrent qu’il s’agit d’un cas particulier de conduction thermique , appelé « conduction avec mouvement fluide ». D’un autre côté, il est pratique de reconnaître la convection comme un mécanisme de transfert de chaleur distinct malgré les arguments valides contraires.

La convection implique le transfert de chaleur entre une surface à une température donnée ( _paroi T ) et un fluide à une température globale (T _b ). La définition exacte de la température globale (T _b ) varie en fonction des détails de la situation.

• Pour un écoulement adjacent à une surface chaude ou froide, T _b est la température du fluide «loin» de la surface.
• Pour l’ébullition ou la condensation, T _b est la température de saturation du fluide.
• Pour l’écoulement dans une conduite, T _b est la température moyenne mesurée à une section particulière de la conduite.

Loi de Newton sur le refroidissement

Malgré la complexité de la convection , le taux de transfert de chaleur par convection est proportionnel à la différence de température et est commodément exprimé par la loi de Newton du refroidissement , qui stipule que:

Le taux de perte de chaleur d’un corps est directement proportionnel à la différence de température entre le corps et son environnement à condition que la différence de température soit petite et que la nature de la surface rayonnante reste la même.

Notez que, ΔT est donné par la température de surface ou de paroi , T _paroi et la température de masse , T _∞ , qui est la température du fluide suffisamment éloignée de la surface.

Coefficient de transfert de chaleur par convection

Comme on peut le voir, la constante de proportionnalité sera cruciale dans les calculs et elle est connue comme le coefficient de transfert de chaleur convectif , h . Le coefficient de transfert de chaleur par convection, h, peut être défini comme:

Le taux de transfert de chaleur entre une surface solide et un fluide par unité de surface par unité de différence de température.

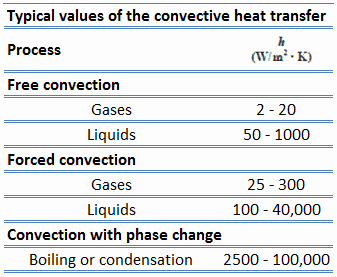Le coefficient de transfert de chaleur convectif dépend des propriétés physiques du fluide et de la situation physique. Le coefficient de transfert de chaleur convectif n’est pas une propriété du fluide. Il s’agit d’un paramètre déterminé expérimentalement dont la valeur dépend de toutes les variables influençant la convection telles que la géométrie de la surface , la nature du mouvement du fluide , les propriétés du fluide et la vitesse du fluide en vrac .

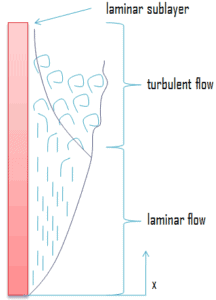
Typiquement, le coefficient de transfert de chaleur par convection pour un écoulement laminaire est relativement faible par rapport au coefficient de transfert de chaleur par convection pour un écoulement turbulent . Cela est dû à un écoulement turbulent ayant une couche de film fluide stagnante plus mince sur la surface de transfert de chaleur.

Il est à noter que cette couche de film fluide stagnant joue un rôle crucial pour le coefficient de transfert thermique convectif. On observe que le fluide s’arrête complètement à la surface et prend une vitesse nulle par rapport à la surface. Ce phénomène est connu sous le nom de condition antidérapante et donc, à la surface, le flux d’énergie se produit uniquement par conduction. Mais dans les couches suivantes, il se produit à la fois un mouvement de conduction et de diffusion-masse au niveau moléculaire ou au niveau macroscopique. En raison du mouvement de masse, le taux de transfert d’énergie est plus élevé. Comme il a été écrit, ébullition nuclééeà la surface perturbe efficacement cette couche stagnante et, par conséquent, l’ébullition nucléée augmente considérablement la capacité d’une surface à transférer l’ énergie thermique au fluide en vrac.

Un phénomène similaire se produit pour la température. On observe que la température du fluide à la surface et la surface auront la même température au point de contact. Ce phénomène est connu sous le nom de condition sans saut de température et il est très important pour la théorie de l’ébullition nucléée .

Les valeurs du coefficient de transfert de chaleur , h, ont été mesurées et tabulées pour les fluides couramment rencontrés et les situations d’écoulement se produisant pendant le transfert de chaleur par convection.

Numéro Nusselt

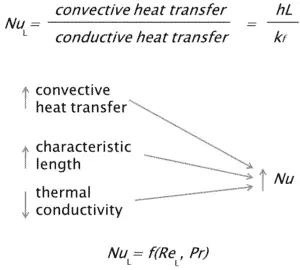
Le nombre de Nusselt est un nombre sans dimension, nommé d’après un ingénieur allemand Wilhelm Nusselt. Le nombre de Nusselt est étroitement lié au nombre de Péclet et les deux nombres sont utilisés pour décrire le rapport de l’ énergie thermique convectée au fluide à l’ énergie thermique conduite dans le fluide. Le nombre de Nusselt est égal au gradient de température sans dimension à la surface, et il fournit une mesure du transfert de chaleur par convection se produisant à la surface. La composante conductrice est mesurée dans les mêmes conditions que la convection thermique mais avec un fluide stagnant. Le numéro de Nusseltest à la couche limite thermique ce que le coefficient de frottement est à la couche limite de vitesse. Ainsi, le nombre de Nusselt est défini comme:

où:

k _f est la conductivité thermique du fluide [W / mK]

L est la longueur caractéristique

h est le coefficient de transfert de chaleur par convection [W / m ² .K]

À titre d’illustration, considérons une couche fluide d’épaisseur L et de différence de température ΔT . Le transfert de chaleur à travers la couche de fluide se fera par convection lorsque le fluide implique un certain mouvement et par conduction lorsque la couche de fluide est immobile.

En cas de conduction , le flux de chaleur peut être calculé en utilisant la loi de conduction de Fourier . En cas de convection, le flux de chaleur peut être calculé en utilisant la loi de Newton du refroidissement. Prendre leur rapport donne:

L’équation précédente définit le nombre de Nusselt . Par conséquent, le nombre de Nusselt représente l’amélioration du transfert de chaleur à travers une couche de fluide en raison de la convection relative à la conduction à travers la même couche de fluide. Un nombre de Nusselt de Nu = 1 pour une couche fluide représente le transfert de chaleur à travers la couche par conduction pure . Plus le nombre de Nusselt est élevé , plus la convection est efficace. Un nombre de Nusselt plus grand correspond à une convection plus efficace, avec un écoulement turbulent typiquement dans la gamme 100–1000. Pour un écoulement turbulent, le nombre de Nusselt est généralement fonction du nombre de Reynolds et duNuméro Prandtl .

Exemple – Transfert de chaleur par convection – Température de surface du revêtement

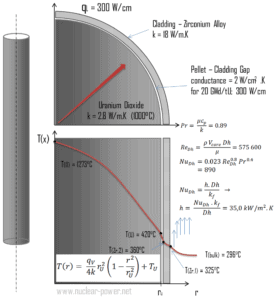Le revêtement est la couche externe des crayons de combustible, se trouvant entre le liquide de refroidissement du réacteur et le combustible nucléaire (c’est-à-dire les pastilles de combustible ). Il est fait d’un matériau résistant à la corrosion avec une faible section d’absorption pour les neutrons thermiques , généralement en alliage de zirconium . Le revêtement empêche les produits de fission radioactifs de s’échapper de la matrice de combustible dans le liquide de refroidissement du réacteur et de le contaminer. Le revêtement constitue l’un des obstacles à l’ approche de « défense en profondeur », donc sa refroidissabilité est l’un des aspects clés de la sécurité.

Considérons la gaine de combustible du rayon intérieur r _{Zr, 2} = 0,408 cm et du rayon extérieur r _{Zr, 1} = 0,465 cm . Par rapport à la pastille de combustible, il n’y a presque pas de génération de chaleur dans la gaine de combustible (la gaine est légèrement chauffée par rayonnement ). Toute la chaleur générée dans le carburant doit être transférée par conduction à travers le revêtement et, par conséquent, la surface intérieure est plus chaude que la surface extérieure.

Suppose que:

• le diamètre extérieur du revêtement est: d = 2 xr _{Zr, 1} = 9,3 mm
• le pas des goupilles de combustible est: p = 13 mm
• la conductivité thermique de l’ eau saturée à 300 ° C est: k _H2O = 0,545 W / mK
• la viscosité dynamique de l’eau saturée à 300 ° C est: μ = 0,0000859 Ns / m ²
• la densité du fluide est: ρ = 714 kg / m ³
• la chaleur spécifique est: c _p = 5,65 kJ / kg.K
• la vitesse d’écoulement du cœur est constante et égale à V _cœur = 5 m / s
• la température du liquide de refroidissement du réacteur à cette coordonnée axiale est: T en _vrac = 296 ° C
• le taux de chaleur linéaire du combustible est q _L = 300 W / cm (F _Q ≈ 2.0) et donc le taux de chaleur volumétrique est q _V = 597 x 10 ⁶ W / m ³

Calculez le nombre de Prandtl , Reynolds et Nusselt pour ce régime d’écoulement (écoulement turbulent forcé interne) à l’intérieur du réseau rectangulaire de combustible (canal de combustible), puis calculez le coefficient de transfert de chaleur et enfin la température de surface de la gaine , T _{Zr, 1} .

Pour calculer la température de surface de la gaine , nous devons calculer le nombre de Prandtl , Reynolds et Nusselt , car le transfert de chaleur pour ce régime d’écoulement peut être décrit par l’ équation de Dittus-Boelter , qui est:

Calcul du nombre de Prandtl

Pour calculer le nombre de Prandtl , nous devons savoir:

• la conductivité thermique de l’eau saturée à 300 ° C est: k _H2O = 0,545 W / mK
• la viscosité dynamique de l’eau saturée à 300 ° C est: μ = 0,0000859 Ns / m ²
• la chaleur spécifique est: c _p = 5,65 kJ / kg.K

Notez que tous ces paramètres diffèrent de manière significative pour l’eau à 300 ° C de ceux à 20 ° C. Le nombre de Prandtl pour l’ eau à 20 ° C est d’environ 6,91. Le nombre de Prandtl pour le liquide de refroidissement du réacteur à 300 ° C est alors:

Calcul du nombre de Reynolds

Pour calculer le nombre de Reynolds, nous devons savoir:

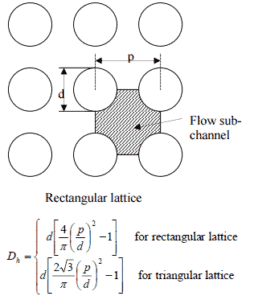
• le diamètre extérieur du revêtement est: d = 2 xr _{Zr, 1} = 9,3 mm (pour calculer le diamètre hydraulique)
• le pas des goupilles de combustible est: p = 13 mm  (pour calculer le diamètre hydraulique)
• la viscosité dynamique de l’eau saturée à 300 ° C est: μ = 0,0000859 Ns / m ²
• la densité du fluide est: ρ = 714 kg / m ³

Le diamètre hydraulique, D _h , est un terme couramment utilisé pour gérer le débit dans des tubes et canaux non circulaires . Le diamètre hydraulique du canal de carburant , D _h , est égal à 13,85 mm.

Voir aussi: Diamètre hydraulique

Le nombre de Reynolds à l’intérieur du canal de carburant est alors égal à:

Cela satisfait pleinement les conditions turbulentes .

Calcul du nombre de Nusselt à l’aide de l’équation de Dittus-Boelter

Pour un écoulement turbulent pleinement développé (hydrodynamiquement et thermiquement) dans un tube circulaire lisse, le nombre de Nusselt local peut être obtenu à partir de l’ équation bien connue de Dittus ?? Boelter .

Pour calculer le nombre de Nusselt , nous devons savoir:

• le nombre de Reynolds , qui est Re _Dh = 575600
• le nombre de Prandtl , qui est Pr = 0,89

Le nombre de Nusselt pour la convection forcée à l’intérieur du canal de carburant est alors égal à:

Calcul du coefficient de transfert de chaleur et de la température de surface du revêtement, T _{Zr, 1}

Une connaissance détaillée de la géométrie, des paramètres des fluides, du rayon extérieur du revêtement, du taux de chaleur linéaire, du coefficient de transfert de chaleur par convection nous permet de calculer la différence de température ∆T entre le liquide de refroidissement (T en _vrac ) et la surface du revêtement (T _{Zr, 1} ).

Pour calculer la température de surface de la gaine, il faut savoir:

• le diamètre extérieur du revêtement est: d = 2 x r _{Zr, 1} = 9,3 mm
• le nombre de Nusselt, qui est Nu _Dh = 890
• le diamètre hydraulique du canal de carburant est: D _h = 13,85 mm
• la conductivité thermique du liquide de refroidissement du réacteur (300 ° C) est: k _H2O = 0,545 W / mK
• la température en vrac du liquide de refroidissement du réacteur à cette coordonnée axiale est: T en _vrac = 296 ° C
• le taux de chaleur linéaire du combustible est: q _L = 300 W / cm (F _Q ≈ 2.0)

Le coefficient de transfert de chaleur par convection, h , est donné directement par la définition du nombre de Nusselt:

Enfin, nous pouvons calculer la température de surface de la gaine (T _{Zr, 1} ) simplement en utilisant la loi de Newton du refroidissement :

Pour les REP en fonctionnement normal, il y a une eau liquide comprimée à l’ intérieur du cœur du réacteur, des boucles et des générateurs de vapeur. La pression est maintenue à environ 16 MPa . À cette pression, l’eau bout à environ 350 ° C (662 ° F). Comme on peut le voir, la température de surface T _{Zr, 1} = 325 ° C garantit que même une ébullition sous-refroidie ne se produit pas. Notez que l’ébullition sous-refroidie nécessite T _{Zr, 1} = T _sat . Étant donné que les températures d’entrée de l’eau sont généralement d’environ 290 ° C(554 ° F), il est évident que cet exemple correspond à la partie inférieure du noyau. Aux altitudes plus élevées du cœur, la température globale peut atteindre jusqu’à 330 ° C. La différence de température de 29 ° C peut entraîner une ébullition sous-refroidie (330 ° C + 29 ° C> 350 ° C). D’autre part, l’ ébullition nucléée à la surface perturbe efficacement la couche stagnante et, par conséquent, l’ébullition nucléée augmente considérablement la capacité d’une surface à transférer l’ énergie thermique au fluide en vrac. En conséquence, le coefficient de transfert de chaleur convectif augmente considérablement et donc à des altitudes plus élevées, la différence de température (T _{Zr, 1} – T en _vrac ) diminue considérablement.