Fórmulas da Primeira Lei da Termodinâmica
O aumento da energia interna de um sistema fechado é igual ao calor fornecido ao sistema menos o trabalho realizado por ele.
Fórmula:
IntE int = Q – W
Esta é a Primeira Lei da Termodinâmica e é o princípio da conservação de energia , o que significa que a energia não pode ser criada nem destruída , mas transformada em várias formas à medida que o fluido dentro do volume de controle está sendo estudado.
É a lei mais importante para análise da maioria dos sistemas e a que quantifica como a energia térmica é transformada em outras formas de energia . Segue-se que máquinas perpétuas de movimento do primeiro tipo são impossíveis.
Forma diferencial:
Forma diferencial:
dE int = dQ – dW
A energia interna E int de um sistema tende a aumentar se a energia é adicionada como calor Q e tende a diminuir se a energia é perdida como o trabalho W realizado pelo sistema.
Primeira lei em termos de entalpia dH = dQ + Vdp
A entalpia é definida como sendo a soma da energia interna E mais o produto da pressão P e volume V . Em muitas análises termodinâmicas, a soma da energia interna U e o produto da pressão pe volume V aparece; portanto, é conveniente atribuir à combinação um nome, entalpia e um símbolo distinto, H.
H = U + pV
Veja também: Entalpia
A primeira lei da termodinâmica em termos de entalpia mostra-nos por que os engenheiros usam a entalpia em ciclos termodinâmicos (por exemplo, ciclo de Brayton ou ciclo de Rankine ).
A forma clássica da lei é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira .
Como H = U + pV , portanto dH = dU + pdV + Vdp e substituímos dU = dH – pdV – Vdp na forma clássica da lei:dH – pdV – Vdp = dQ – pdV
Obtemos a lei em termos de entalpia:
dH = dQ + Vdp
ou
dH = TdS + Vdp
Nesta equação, o termo Vdp é um trabalho de processo de fluxo. Este trabalho, Vdp , é usado para sistemas de fluxo aberto, como uma turbina ou uma bomba na qual existe um “dp” , ou seja, mudança de pressão. Não há alterações no volume de controle . Como pode ser visto, essa forma de lei simplifica a descrição da transferência de energia . A pressão constante , a mudança de entalpia é igual à energia transferida do ambiente através do aquecimento:
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no ou pelo sistema:
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
É óbvio que será muito útil na análise de ambos os ciclos termodinâmicos usados na engenharia de energia, ou seja, no ciclo de Brayton e no ciclo de Rankine.
Trabalho pΔV
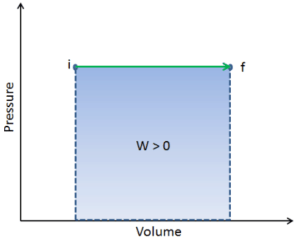
Exemplo:
Considere-se um pistão de atrito que é usado para proporcionar uma pressão constante de 500 kPa num cilindro contendo vapor ( vapor sobreaquecido ) de um volume de 2 m 3 a 500 K .
Calcule a temperatura final, se 3000 kJ de calor forem adicionados.
Solução:
Usando tabelas de vapor , sabemos que a entalpia específica desse vapor (500 kPa; 500 K) é de cerca de 2912 kJ / kg . Como nessa condição o vapor possui densidade de 2,2 kg / m 3 , sabemos que há cerca de 4,4 kg de vapor no pistão na entalpia de 2912 kJ / kg x 4,4 kg = 12812 kJ .
Quando usamos simplesmente Q = H 2 – H 1 , a entalpia resultante do vapor será:
H 2 = H 1 + Q = 15812 kJ
Nas tabelas de vapor , esse vapor superaquecido (15812 / 4,4 = 3593 kJ / kg) terá uma temperatura de 828 K (555 ° C) . Uma vez que nesta entalpia do vapor tem a densidade de 1,31 kg / m 3 , é óbvio que se expandiu em cerca de 2,2 / 1,31 = 1,67 (+ 67%). Portanto, o volume resultante é de 2 m 3 x 1,67 = 3,34 m 3 e ∆V = 3,34 m 3 – 2 m 3 = 1,34 m 3 .
A parte p∆V da entalpia, ou seja, o trabalho realizado é:
W = p∆V = 500 000 Pa x 1,34 m 3 = 670 kJ
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.