Fórmulas de la primera ley de la termodinámica.
El aumento de la energía interna de un sistema cerrado es igual al calor suministrado al sistema menos el trabajo realizado por él.
Fórmula:
IntE int = Q – W
Esta es la primera ley de la termodinámica y es el principio de conservación de la energía , lo que significa que la energía puede ser creada ni destruida , sino más bien transforma en diversas formas como se está estudiando el fluido dentro del volumen de control.
Es la ley más importante para el análisis de la mayoría de los sistemas y la que cuantifica cómo se transforma la energía térmica en otras formas de energía . De ello se deduce que las máquinas de movimiento perpetuo del primer tipo son imposibles.
Forma diferencial:
Forma diferencial:
dE int = dQ – dW
La energía interna E int de un sistema tiende a aumentar si se agrega energía como calor Q y tiende a disminuir si la energía se pierde como trabajo W realizado por el sistema.
Primera ley en términos de entalpía dH = dQ + Vdp
La entalpía se define para ser la suma de la energía interna E más el producto de la presión p y el volumen V . En muchos análisis termodinámicos aparece la suma de la energía interna U y el producto de la presión py el volumen V, por lo tanto, es conveniente dar a la combinación un nombre, entalpía y un símbolo distintivo, H.
H = U + pV
Ver también: entalpía
La primera ley de la termodinámica en términos de entalpía nos muestra por qué los ingenieros usan la entalpía en ciclos termodinámicos (por ejemplo, el ciclo de Brayton o el ciclo de Rankine ).
La forma clásica de la ley es la siguiente ecuación:
dU = dQ – dW
En esta ecuación, dW es igual a dW = pdV y se conoce como el trabajo límite .
Obtenemos la ley en términos de entalpía:
dH = dQ + Vdp
o
dH = TdS + Vdp
En esta ecuación, el término Vdp es un proceso de flujo de trabajo. Este trabajo, Vdp , se utiliza para sistemas de flujo abierto como una turbina o una bomba en la que hay un “dp” , es decir, un cambio de presión. No hay cambios en el volumen de control . Como puede verse, esta forma de ley simplifica la descripción de la transferencia de energía . A presión constante , el cambio de entalpía es igual a la energía transferida del ambiente a través del calentamiento:
Proceso isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
En una entropía constante , es decir, en un proceso isentrópico, el cambio de entalpía es igual al trabajo del proceso de flujo realizado en o por el sistema:
Proceso isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1
Es obvio, será muy útil en el análisis de los dos ciclos termodinámicos utilizados en la ingeniería de energía, es decir, en el ciclo de Brayton y el ciclo de Rankine.
pΔV trabajo
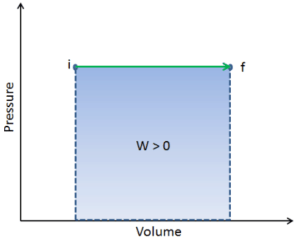
Ejemplo:
Considere un pistón sin fricción que se utiliza para proporcionar una presión constante de 500 kPa en un cilindro que contiene vapor de agua ( vapor sobrecalentado ) de un volumen de 2 m 3 a 500 K .
Calcule la temperatura final, si se agregan 3000 kJ de calor .
Solución:
Usando tablas de vapor , sabemos que la entalpía específica de dicho vapor (500 kPa; 500 K) es de aproximadamente 2912 kJ / kg . Como en esta condición el vapor tiene una densidad de 2.2 kg / m 3 , entonces sabemos que hay alrededor de 4.4 kg de vapor en el pistón a una entalpía de 2912 kJ / kg x 4.4 kg = 12812 kJ .
Cuando usamos simplemente Q = H 2 – H 1 , la entalpía de vapor resultante será:
H 2 = H 1 + Q = 15812 kJ
De las mesas de vapor , dicho vapor sobrecalentado (15812 / 4.4 = 3593 kJ / kg) tendrá una temperatura de 828 K (555 ° C) . Dado que en esta entalpía el vapor tiene una densidad de 1.31 kg / m 3 , es obvio que se ha expandido aproximadamente 2.2 / 1.31 = 1.67 (+ 67%). Por lo tanto, el volumen resultante es 2 m 3 x 1.67 = 3.34 m 3 y ∆V = 3.34 m 3 – 2 m 3 = 1.34 m 3 .
La parte p∆V de la entalpía, es decir, el trabajo realizado es:
W = p∆V = 500 000 Pa x 1.34 m 3 = 670 kJ
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.