Equação de Bernoulli
A equação de Bernoulli pode ser considerada uma afirmação do princípio de conservação de energia apropriado para fluidos fluidos. É uma das equações mais importantes / úteis na mecânica de fluidos . Ele coloca em uma relação pressão e velocidade um fluxo incompreensível inviscível . A equação de Bernoulli tem algumas restrições em sua aplicabilidade, resumidas nos seguintes pontos:
- sistema de fluxo constante,
- a densidade é constante (o que também significa que o fluido é incompressível),
- nenhum trabalho é feito sobre ou pelo fluido,
- nenhum calor é transferido para ou a partir do fluido,
- nenhuma mudança ocorre na energia interna,
- a equação relaciona os estados em dois pontos ao longo de uma única linha de fluxo (não condições em duas linhas de fluxo diferentes)
Sob essas condições, a equação geral de energia é simplificada para:
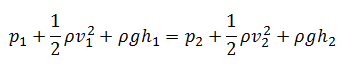
Essa equação é a mais famosa da dinâmica de fluidos . A equação de Bernoulli descreve o comportamento qualitativo que flui fluido que geralmente é rotulado com o termo efeito de Bernoulli . Esse efeito causa a redução da pressão do fluido em regiões onde a velocidade do fluxo é aumentada. Esse abaixamento da pressão em uma constrição de um caminho de fluxo pode parecer contra-intuitivo, mas parece menos quando você considera a pressão como densidade de energia. No fluxo de alta velocidade através da constrição, a energia cinética deve aumentar à custa da energia de pressão. As dimensões dos termos na equação são energia cinética por unidade de volume.
Lei de Torricelli
A lei de Torricelli , também conhecida como princípio de Torricelli , ou teorema de Torricelli , afirma na dinâmica dos fluidos que a velocidade, v, do fluido que sai de um orifício sob a força da gravidade em um tanque é proporcional à raiz quadrada da distância vertical, h , entre a superfície do líquido e o centro do orifício e a raiz quadrada do dobro da aceleração causada pela gravidade (g = 9,81 N / kg próximo à superfície da Terra).
Em outras palavras, a velocidade de efluxo do fluido do orifício é a mesma que teria adquirido ao cair uma altura h abaixo da gravidade. A lei foi descoberta e nomeada em homenagem ao cientista italiano Evangelista Torricelli , em 1643. Mais tarde, mostrou-se um caso particular do princípio de Bernoulli .
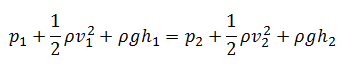
A equação de Torricelli é derivada para uma condição específica. O orifício deve ser pequeno e a viscosidade e outras perdas devem ser ignoradas. Se um fluido está fluindo através de um orifício muito pequeno (por exemplo, no fundo de um tanque grande), a velocidade do fluido na extremidade maior pode ser negligenciada na Equação de Bernoulli. Além disso, a velocidade do efluxo é independente da direção do fluxo. Nesse caso, a velocidade de efluxo do fluido que flui através do orifício dada pela seguinte fórmula:
v = √ 2gh
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
