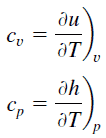O que é capacidade de calor – Capacidade específica de calor – Definição

Capacidade de calor

Diferentes substâncias são afetadas em diferentes magnitudes pela adição de calor . Quando uma determinada quantidade de calor é adicionada a diferentes substâncias, suas temperaturas aumentam em diferentes quantidades. Essa constante de proporcionalidade entre o calor Q que o objeto absorve ou perde e a mudança de temperatura resultante T do objeto é conhecida como capacidade de calor C de um objeto.

C = Q / ΔT

A capacidade de calor é uma propriedade extensa da matéria, o que significa que é proporcional ao tamanho do sistema. A capacidade térmica C tem a unidade de energia por grau ou energia por kelvin. Ao expressar o mesmo fenômeno que uma propriedade intensiva , a capacidade de aquecimento é dividida pela quantidade de substância, massa ou volume, portanto, a quantidade é independente do tamanho ou extensão da amostra.

Capacidade específica de calor

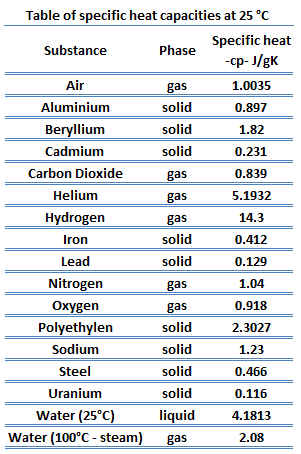
A capacidade térmica de uma substância por unidade de massa é denominada capacidade térmica específica (c _p ) da substância. O índice p indica que a capacidade térmica e a capacidade térmica específica se aplicam quando o calor é adicionado ou removido a pressão constante .

c _p = Q / mΔT

Capacidade de calor específica do gás ideal

No Modelo de Gás Ideal , as propriedades intensivas c _v e c _p são definidas para substâncias compressíveis puras e simples como derivadas parciais da energia interna u (T, v) e entalpia h (T, p) , respectivamente:

onde os subscritos v e p denotam as variáveis ​​mantidas fixas durante a diferenciação. As propriedades c _v e c _p são referidos como calores específicos (ou capacidades de calor ), porque, sob determinadas condições especiais dizem respeito a mudança de temperatura de um sistema para a quantidade de energia adicionada pela transferência de calor. As suas unidades SI são J / kg K ou J / mol K . Dois aquecimentos específicos são definidos para gases, um para volume constante (c _v ) e outro para pressão constante (c _p ) .

De acordo com a primeira lei da termodinâmica , para processos de volume constante com um gás ideal monatômico, o calor molar específico será:

C _v = 3 / 2R = 12,5 J / mol K

Porque

U = 3 / 2nRT

Pode-se derivar que o calor molar específico a pressão constante é:

C _p = C _v + R = 5 / 2R = 20,8 J / mol K

Este C _p é maior do que o calor específico molar a volume constante C _v , porque a energia deve agora ser fornecidos não só para aumentar a temperatura do gás, mas também para o gás de trabalho para fazer porque neste volume caso alterações.