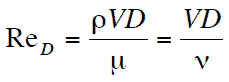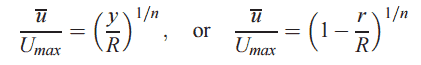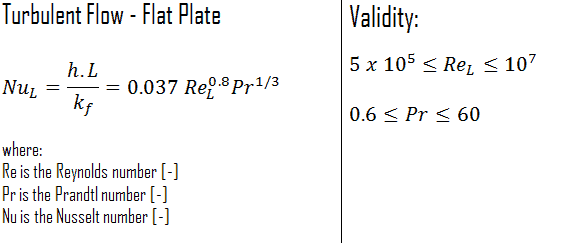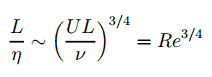Fluxo turbulento
Na dinâmica de fluidos, o fluxo turbulento é caracterizado pelo movimento irregular de partículas (pode-se dizer caótico ) do fluido. Ao contrário do fluxo laminar, o fluido não flui em camadas paralelas, a mistura lateral é muito alta e há uma ruptura entre as camadas. A turbulência também é caracterizada por recirculação, redemoinhos e aleatoriedade aparente . No fluxo turbulento, a velocidade do fluido em um ponto está continuamente sofrendo alterações na magnitude e na direção.
O conhecimento detalhado do comportamento do regime de fluxo turbulento é importante na engenharia, porque a maioria dos fluxos industriais , especialmente os de engenharia nuclear, são turbulentos . Infelizmente, o caráter altamente intermitente e irregular da turbulência complica todas as análises . De fato, costuma-se dizer que a turbulência é o “último problema não resolvido da física matemática clássica”.
A principal ferramenta disponível para sua análise é a análise CFD . O CFD é um ramo da mecânica de fluidos que utiliza análise e algoritmos numéricos para resolver e analisar problemas que envolvem fluxos de fluidos turbulentos. É amplamente aceito que as equações de Navier-Stokes (ou equações simplificadas de Navier-Stokes, com média de Reynolds ) são capazes de exibir soluções turbulentas, e essas equações são a base de praticamente todos os códigos CFD.
Veja também: Fluxo interno
Veja também: Fluxo externo
Características do fluxo turbulento
- O fluxo turbulento tende a ocorrer em velocidades mais altas , baixa viscosidade e em dimensões lineares características mais altas .
- Se o número de Reynolds for maior que Re> 3500, o fluxo será turbulento.
- Irregularidade: O fluxo é caracterizado pelo movimento irregular das partículas do fluido. O movimento de partículas fluidas é caótico. Por esse motivo, o fluxo turbulento é normalmente tratado estatisticamente, e não deterministicamente.
- Difusividade: No fluxo turbulento, existe uma distribuição de velocidade bastante plana na seção do tubo, com o resultado de que todo o fluido flui em um determinado valor único e cai rapidamente extremamente perto das paredes. A característica responsável pela mistura aprimorada e aumento das taxas de transporte de massa, momento e energia em um fluxo é chamada de “difusividade”.
- Rotacionalidade: O fluxo turbulento é caracterizado por um forte mecanismo tridimensional de geração de vórtices. Esse mecanismo é conhecido como alongamento por vórtice.
- Dissipação: Um processo dissipativo é um processo no qual a energia cinética do fluxo turbulento é transformada em energia interna por tensão de cisalhamento viscoso.
Número de Reynolds
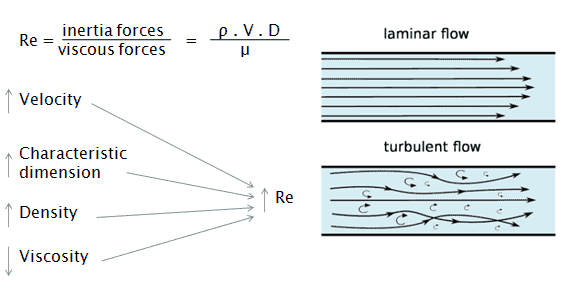
O número de Reynoldsé a proporção de forças de inércia para as forças viscosas e é um parâmetro conveniente para prever se uma condição de escoamento vai ser laminar ou turbulento . Pode-se interpretar que quando as forças viscosas são dominantes (fluxo lento, Re baixo) são suficientes o suficiente para manter todas as partículas de fluido alinhadas, então o fluxo é laminar. Mesmo Re muito baixo indica movimento de rastejamento viscoso, onde os efeitos de inércia são desprezíveis. Quando as forças inerciais dominam sobre as forças viscosas (quando o fluido está fluindo mais rápido e Re é maior), então o fluxo é turbulento.
É um número sem dimensão composto pelas características físicas do fluxo. Um número crescente de Reynolds indica uma crescente turbulência do fluxo.
É definido como:
em que:
V é a velocidade do fluxo,
D é uma dimensão linear característica (comprimento percorrido do fluido; diâmetro hidráulico etc.)
ρ densidade do fluido (kg / m 3 ),
μ viscosidade dinâmica (Pa.s),
ν viscosidade cinemática ( m 2 / s); ν = μ / ρ.
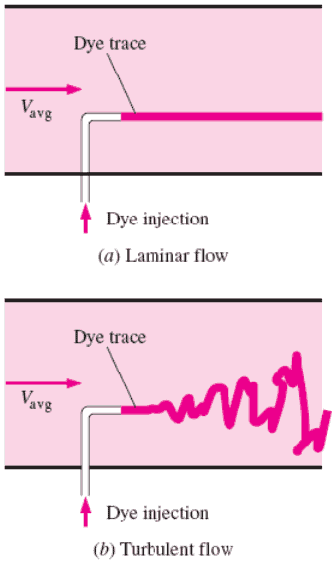
Fluxo Laminar vs. Turbulento
Fluxo laminar:
- Re <2000
- velocidade ‘baixa’
- Partículas fluidas se movem em linhas retas
- Camadas de água fluem umas sobre as outras em velocidades diferentes, praticamente sem mistura entre as camadas.
- O perfil da velocidade do fluxo para o fluxo laminar em tubos circulares é parabólico, com um fluxo máximo no centro do tubo e um fluxo mínimo nas paredes do tubo.
- A velocidade média do fluxo é aproximadamente metade da velocidade máxima.
- É possível uma análise matemática simples.
- Raro na prática em sistemas de água .
Fluxo turbulento:
- Re> 4000
- ‘alta velocidade
- O fluxo é caracterizado pelo movimento irregular de partículas do fluido.
- O movimento médio está na direção do fluxo
- O perfil de velocidade do fluxo para turbulência é bastante plano através da seção central de um tubo e cai rapidamente extremamente perto das paredes.
- A velocidade média do fluxo é aproximadamente igual à velocidade no centro do tubo.
- A análise matemática é muito difícil.
- Tipo mais comum de fluxo .
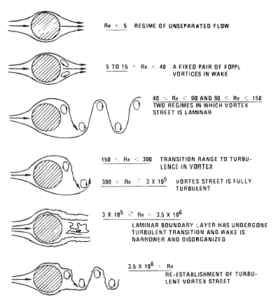
Fonte: Blevins, RD (1990), Vibração induzida por fluxo, 2ª Edição, Van Nostrand Reinhold Co.
Perfil de velocidade turbulenta
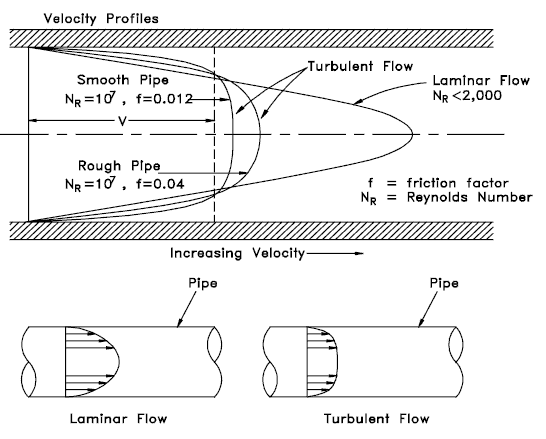
Perfil de velocidade da lei de potência – Perfil de velocidade turbulenta
O perfil de velocidade no fluxo turbulento é mais plano na parte central do tubo (ou seja, no núcleo turbulento) do que no fluxo laminar . A velocidade do fluxo cai rapidamente extremamente perto das paredes. Isto é devido à difusividade do fluxo turbulento.
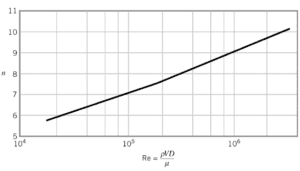
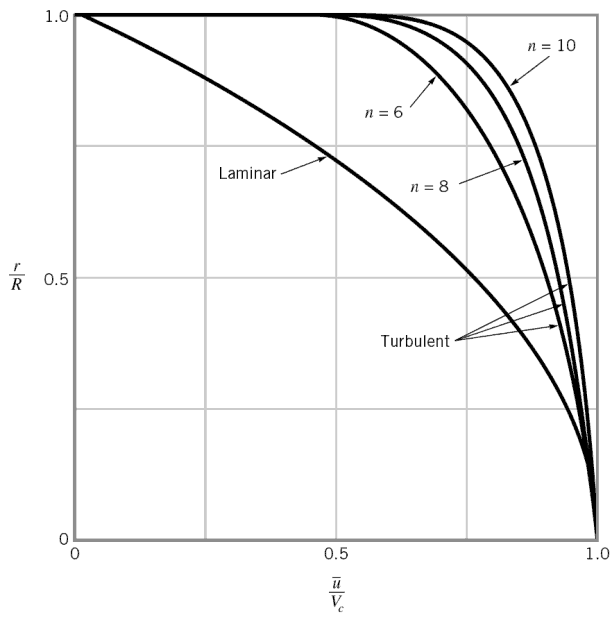
No caso de fluxo de tubulação turbulento, existem muitos perfis de velocidade empíricos. O mais simples e mais conhecido é o perfil de velocidade da lei de potência :
onde o expoente n é uma constante cujo valor depende do número de Reynolds . Essa dependência é empírica e é mostrada na figura. Em resumo, o valor n aumenta com o aumento do número de Reynolds. O sétimo perfil de velocidade da lei da potência aproxima muitos fluxos industriais.
Exemplos de fluxo turbulento
Camada limite turbulenta
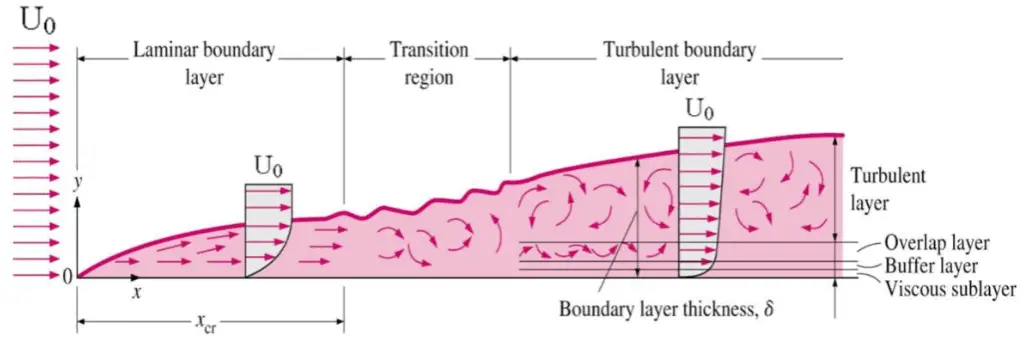
O conceito de camadas limite é importante em toda a dinâmica de fluidos viscosos, aerodinâmica e também na teoria da transferência de calor. As características básicas de todas as camadas limite laminar e turbulenta são mostradas no fluxo em desenvolvimento sobre uma placa plana. Os estágios da formação da camada limite são mostrados na figura abaixo:
As camadas de limite podem ser laminares ou turbulentas, dependendo do valor do número de Reynolds . Também aqui o número de Reynolds representa a razão entre forças de inércia e forças viscosas e é um parâmetro conveniente para prever se uma condição de fluxo será laminar ou turbulenta. É definido como:
em que V é a velocidade média do fluxo, D uma dimensão linear característica, ρ densidade do fluido, μ viscosidade dinâmica e ν viscosidade cinemática.
Para números mais baixos de Reynolds , a camada limite é laminar e a velocidade no sentido do fluxo muda uniformemente à medida que se afasta da parede, conforme mostrado no lado esquerdo da figura. À medida que o número de Reynolds aumenta (com x), o fluxo se torna instável e, finalmente, para números mais altos de Reynolds, a camada limite é turbulenta e a velocidade do fluxo é caracterizada por fluxos instáveis (mudando com o tempo) dentro da camada limite.
A transição da camada limite laminar para a turbulenta ocorre quando o número de Reynolds em x excede Re x ~ 500.000 . A transição pode ocorrer mais cedo, mas depende principalmente da rugosidade da superfície . A camada limite turbulenta espessa mais rapidamente do que a camada limite laminar como resultado do aumento da tensão de cisalhamento na superfície do corpo.
Veja também: Espessura da camada limite
Veja também: Tubo em fluxo cruzado – fluxo externo
Referência especial: Schlichting Herrmann, Gersten Klaus. Teoria da camada limite, Springer-Verlag Berlin Heidelberg, 2000, ISBN: 978-3-540-66270-9
Fluxo Turbulento – Coeficiente de Transferência de Calor
Fluxo Turbulento Externo
O númeromédio de Nusselt em toda a placa é determinado por:
Essa relação fornece o coeficiente médio de transferência de calor para a placa inteira somente quando o fluxo é turbulentosobre a placa inteira ou quando a região de fluxo laminar da placa é muito pequena em relação à região do fluxo turbulento.
Fluxo Turbulento Interno – Dittus-Boelter
Veja também: Equação de Dittus-Boelter
Para um fluxo turbulento totalmente desenvolvido (hidrodinamicamente e termicamente) em um tubo circular liso, o número local de Nusselt pode ser obtido a partir da conhecida equação de Dittus-Boelter . A equação Dittus® Boelter é fácil de resolver, mas é menos precisa quando existe uma grande diferença de temperatura no fluido e é menos precisa para tubos ásperos (muitas aplicações comerciais), pois é adaptada para tubos lisos.
A correlação de Dittus-Boelter pode ser usada para diferenças de temperatura pequenas a moderadas, T wall – T avg , com todas as propriedades avaliadas a uma temperatura média T avg .
Para fluxos caracterizados por grandes variações de propriedades, as correções (por exemplo, um fator de correção de viscosidade μ / μ de parede ) devem ser levadas em consideração, por exemplo, como recomendam Sieder e Tate .
Kolmogorov Microscales
Na visão de Kolmogorov ( Andrey Nikolaevich Kolmogorov era um matemático russo que fez contribuições significativas para a matemática da teoria das probabilidades e da turbulência), movimentos turbulentos envolvem uma ampla gama de escalas . De uma macroescala na qual a energia é fornecida, a uma microescala na qual a energia é dissipada pela viscosidade.
Por exemplo, considere uma nuvem cumulus. A macroescala da nuvem pode ser da ordem de quilômetros e pode crescer ou persistir por longos períodos de tempo. Dentro da nuvem, redemoinhos podem ocorrer em escalas da ordem de milímetros . Para fluxos menores, como em tubos, as micro-escalas podem ser muito menores. A maior parte da energia cinética do fluxo turbulento está contida nas estruturas de macroescala. A energia “cascata” dessas estruturas de macroescala para estruturas de microescala por um mecanismo inercial. Esse processo é conhecido como cascata de energia turbulenta .
As menores escalas em fluxo turbulento são conhecidas como microescalas Kolmogorov . Elas são pequenas o suficiente para que a difusão molecular se torne importante e ocorre a dissipação viscosa da energia e a energia cinética turbulenta é dissipada no calor.
As menores escalas em fluxo turbulento, ou seja, as microescalas Kolmogorov são:
onde ε é a taxa média de taxa de dissipação da energia cinética da turbulência por unidade de massa e tem dimensões (m 2 / s 3 ). ν é a viscosidade cinemática do fluido e possui dimensões (m 2 / s).
O tamanho do menor redemoinho no fluxo é determinado pela viscosidade. A escala de comprimento de Kolmogorov diminui à medida que a viscosidade diminui. Para fluxos de números Reynolds muito altos , as forças viscosas são menores em relação às forças inerciais. Movimentos de menor escala são necessariamente gerados até que os efeitos da viscosidade se tornem importantes e a energia seja dissipada. A proporção entre as escalas de maior e menor comprimento no fluxo turbulento é proporcional ao número de Reynolds (aumenta com a potência de três quartos ).
Isso faz com que simulações numéricas diretas de fluxo turbulento sejam praticamente impossíveis. Por exemplo, considere um fluxo com um número de Reynolds de 10 6 . Nesse caso, a razão L / l é proporcional a 10 18/4 . Como temos que analisar o problema tridimensional, precisamos calcular uma grade que consiste em pelo menos 10 14 pontos de grade . Isso excede em muito a capacidade e as possibilidades dos computadores existentes.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
