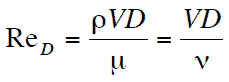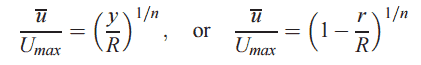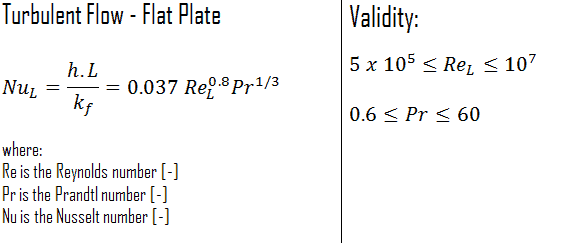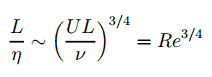Écoulement turbulent
En dynamique des fluides, l’ écoulement turbulent est caractérisé par le mouvement irrégulier des particules (on peut dire chaotique ) du fluide. Contrairement au flux laminaire, le fluide ne coule pas en couches parallèles, le mélange latéral est très élevé et il y a une rupture entre les couches. La turbulence est également caractérisée par la recirculation, les tourbillons et le caractère aléatoire apparent . Dans un écoulement turbulent, la vitesse du fluide en un point subit continuellement des changements d’amplitude et de direction.
Une connaissance détaillée du comportement du régime d’écoulement turbulent est importante en génie, car la plupart des écoulements industriels , en particulier ceux du génie nucléaire, sont turbulents . Malheureusement, le caractère hautement intermittent et irrégulier des turbulences complique toutes les analyses . En fait, la turbulence est souvent considérée comme le «dernier problème non résolu de la physique mathématique classique».
Le principal outil disponible pour leur analyse est l’ analyse CFD . CFD est une branche de la mécanique des fluides qui utilise l’analyse numérique et des algorithmes pour résoudre et analyser les problèmes impliquant des écoulements de fluide turbulents. Il est largement admis que les équations de Navier-Stokes (ou les équations simplifiées de Navier-Stokes moyennées par Reynolds ) sont capables de présenter des solutions turbulentes, et ces équations sont la base de pratiquement tous les codes CFD.
Voir aussi: Flux interne
Voir aussi: Flux externe
Caractéristiques du flux turbulent
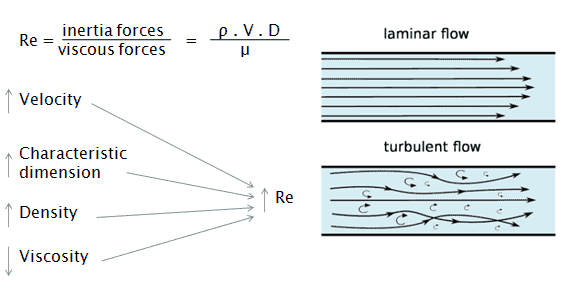
- Un écoulement turbulent a tendance à se produire à des vitesses plus élevées , à une faible viscosité et à des dimensions linéaires caractéristiques plus élevées .
- Si le nombre de Reynolds est supérieur à Re> 3500, l’écoulement est turbulent.
- Irrégularité: L’écoulement est caractérisé par le mouvement irrégulier des particules du fluide. Le mouvement des particules fluides est chaotique. Pour cette raison, l’écoulement turbulent est normalement traité statistiquement plutôt que de manière déterministe.
- Diffusivité: Dans un écoulement turbulent, une distribution de vitesse assez plate existe à travers la section du tuyau, avec pour résultat que le fluide entier s’écoule à une valeur unique donnée et tombe rapidement extrêmement près des parois. La caractéristique qui est responsable du mélange amélioré et des taux accrus de transports de masse, de quantité de mouvement et d’énergie dans un écoulement est appelée «diffusivité».
- Rotationalité: l’ écoulement turbulent est caractérisé par un puissant mécanisme de génération de vortex tridimensionnel. Ce mécanisme est connu sous le nom d’étirement vortex.
- Dissipation: Un processus dissipatif est un processus dans lequel l’énergie cinétique de l’écoulement turbulent est transformée en énergie interne par une contrainte de cisaillement visqueuse.
Le numéro de Reynold
Le nombre de Reynolds est le rapport des forces d’ inertie aux forces visqueuses et est un paramètre commode pour prédire si une condition d’écoulement sera laminaire ou turbulent . On peut interpréter que lorsque les forces visqueuses sont dominantes (flux lent, Re faible) elles sont suffisantes pour maintenir toutes les particules de fluide en ligne, alors le flux est laminaire. Même un très faible Re indique un mouvement de fluage visqueux, où les effets d’inertie sont négligeables. Lorsque les forces d’inertie dominent sur les forces visqueuses (lorsque le fluide s’écoule plus rapidement et que Re est plus grand), l’écoulement est turbulent.
Il s’agit d’un nombre sans dimension comprenant les caractéristiques physiques de l’écoulement. Un nombre de Reynolds croissant indique une turbulence croissante de l’écoulement.
où:
V est la vitesse d’écoulement,
D est une dimension linéaire caractéristique , (longueur parcourue du fluide; diamètre hydraulique, etc.)
ρ densité du fluide (kg / m 3 ),
μ viscosité dynamique (Pa.s),
ν viscosité cinématique ( m 2 / s); ν = μ / ρ.
Débit laminaire ou turbulent
Écoulement laminaire:
- Re <2000
- vitesse «faible»
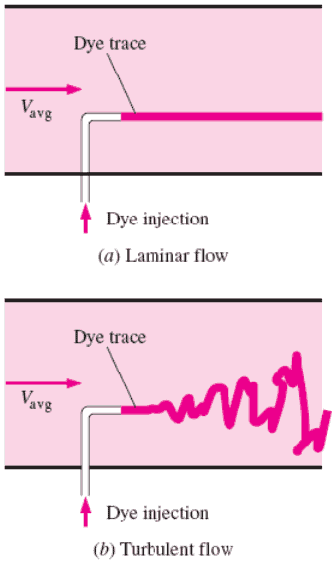
- Les particules fluides se déplacent en ligne droite
- Les couches d’eau s’écoulent les unes sur les autres à différentes vitesses sans pratiquement aucun mélange entre les couches.
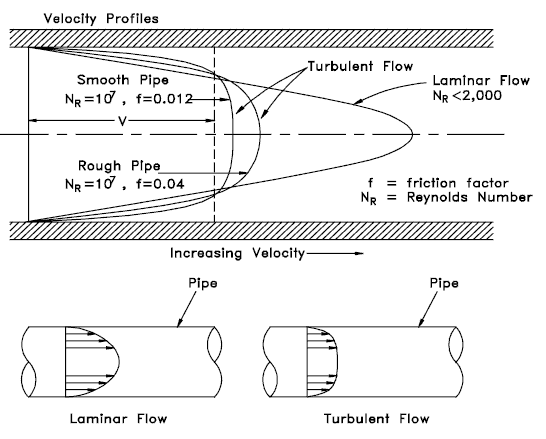
- Le profil de vitesse d’écoulement pour un flux laminaire dans des tuyaux circulaires est de forme parabolique, avec un débit maximal au centre du tuyau et un débit minimal au niveau des parois des tuyaux.
- La vitesse d’écoulement moyenne correspond à environ la moitié de la vitesse maximale.
- Une analyse mathématique simple est possible.
- Rare en pratique dans les systèmes d’eau .
Écoulement turbulent:
- Re> 4000
- ‘vitesse élevée
- L’écoulement est caractérisé par le mouvement irrégulier des particules du fluide.
- Le mouvement moyen est dans le sens de l’écoulement
- Le profil de vitesse d’écoulement pour un écoulement turbulent est assez plat sur la section centrale d’un tuyau et tombe rapidement extrêmement près des parois.
- La vitesse d’écoulement moyenne est approximativement égale à la vitesse au centre du tuyau.
- L’analyse mathématique est très difficile.
- Type d’écoulement le plus courant .
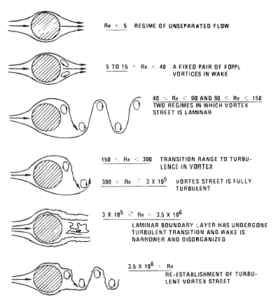
Source: Blevins, RD (1990), Flow Induced Vibration, 2nd Edn., Van Nostrand Reinhold Co.
Profil de vitesse turbulente
Profil de vitesse de loi de puissance – Profil de vitesse turbulent
 Le profil de vitesse en écoulement turbulent est plus plat dans la partie centrale du tuyau (c’est-à-dire dans le cœur turbulent) qu’en écoulement laminaire . La vitesse d’écoulement chute rapidement extrêmement près des murs. Cela est dû à la diffusivité de l’écoulement turbulent.
Le profil de vitesse en écoulement turbulent est plus plat dans la partie centrale du tuyau (c’est-à-dire dans le cœur turbulent) qu’en écoulement laminaire . La vitesse d’écoulement chute rapidement extrêmement près des murs. Cela est dû à la diffusivité de l’écoulement turbulent.
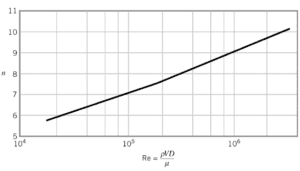
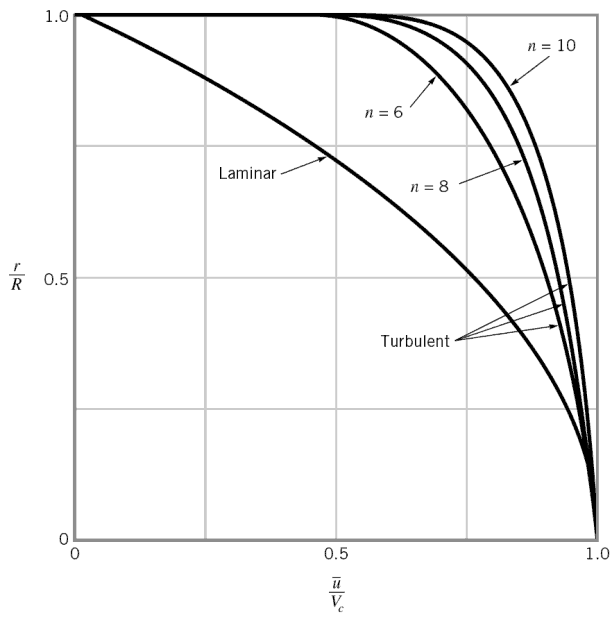
En cas d’écoulement turbulent de tuyaux, il existe de nombreux profils de vitesse empiriques. Le plus simple et le plus connu est le profil de vitesse selon la loi de puissance :
où l’exposant n est une constante dont la valeur dépend du nombre de Reynolds . Cette dépendance est empirique et elle est illustrée sur l’image. En bref, la valeur n augmente avec l’augmentation du nombre de Reynolds. Le septième profil de vitesse selon la loi de puissance se rapproche de nombreux flux industriels.
Exemples d’écoulement turbulent
Couche limite turbulente
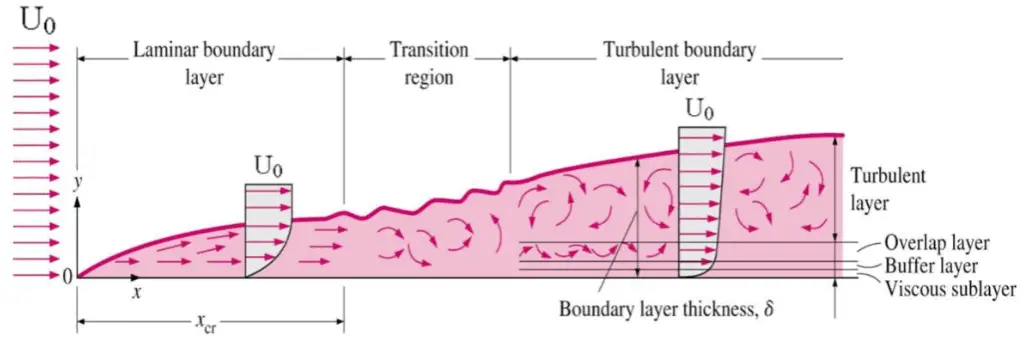
Le concept de couches limites est important dans toute la dynamique des fluides visqueux, l’aérodynamique et aussi dans la théorie du transfert de chaleur. Les caractéristiques de base de toutes les couches limites laminaires et turbulentes sont présentées dans le flux de développement sur une plaque plate. Les étapes de la formation de la couche limite sont illustrées dans la figure ci-dessous:
Les couches limites peuvent être laminaires ou turbulentes selon la valeur du nombre de Reynolds . Ici aussi, le nombre de Reynolds représente le rapport des forces d’inertie aux forces visqueuses et est un paramètre pratique pour prédire si une condition d’écoulement sera laminaire ou turbulente. Il est défini comme:
dans laquelle V est la vitesse d’écoulement moyenne, D une dimension linéaire caractéristique, ρ la densité du fluide, μ la viscosité dynamique et ν la viscosité cinématique.
Pour les nombres de Reynolds inférieurs , la couche limite est laminaire et la vitesse du flux change uniformément lorsque l’on s’éloigne du mur, comme indiqué sur le côté gauche de la figure. À mesure que le nombre de Reynolds augmente (avec x), l’ écoulement devient instable et, enfin, pour les nombres de Reynolds plus élevés, la couche limite est turbulente et la vitesse dans le sens du courant se caractérise par des flux tourbillonnants instables (changeant avec le temps) à l’intérieur de la couche limite.
La transition de la couche limite laminaire à la couche turbulente se produit lorsque le nombre de Reynolds à x dépasse Re x ~ 500 000 . La transition peut se produire plus tôt, mais elle dépend surtout de la rugosité de la surface . La couche limite turbulente s’épaissit plus rapidement que la couche limite laminaire en raison de l’augmentation de la contrainte de cisaillement à la surface du corps.
Voir aussi: Épaisseur de la couche limite
Voir aussi: Tube en flux croisé – flux externe
Référence spéciale: Schlichting Herrmann, Gersten Klaus. Théorie des couches limites, Springer-Verlag Berlin Heidelberg, 2000, ISBN: 978-3-540-66270-9
Écoulement turbulent – Coefficient de transfert de chaleur
Débit turbulent externe
Le nombre moyen de Nusselt sur toute la plaque est déterminé par:
Cette relation donne le coefficient de transfert thermique moyen pour la plaque entière uniquement lorsque l’écoulement est turbulent sur toute la plaque, ou lorsque la région d’ écoulement laminaire de la plaque est trop petite par rapport à la région d’écoulement turbulent.
Débit turbulent interne – Dittus-Boelter
Voir aussi: Équation Dittus-Boelter
Pour un écoulement turbulent complètement développé (hydrodynamiquement et thermiquement) dans un tube circulaire lisse, le nombre de Nusselt local peut être obtenu à partir de l’ équation bien connue de Dittus-Boelter . L’ équation Dittus ?? Boelter est facile à résoudre mais est moins précise lorsqu’il existe une grande différence de température à travers le fluide et est moins précise pour les tubes rugueux (de nombreuses applications commerciales), car elle est adaptée aux tubes lisses.
La corrélation Dittus-Boelter peut être utilisée pour des différences de température petites à modérées, paroi T – T moyenne , toutes les propriétés étant évaluées à une température moyenne T moyenne .
Pour les écoulements caractérisés par de grandes variations de propriétés, les corrections (par exemple un facteur de correction de viscosité μ / μ paroi ) doivent être prises en compte, par exemple, comme le recommandent Sieder et Tate .
Microscales Kolmogorov
De l’avis de Kolmogorov ( Andrey Nikolaevich Kolmogorov était un mathématicien russe qui a apporté une contribution significative aux mathématiques de la théorie des probabilités et de la turbulence), les mouvements turbulents impliquent une large gamme d’échelles . D’une échelle macroscopique à laquelle l’énergie est fournie, à une échelle microscopique à laquelle l’énergie est dissipée par la viscosité.
Par exemple, considérons un nuage cumulus. L’ échelle macroscopique du nuage peut être de l’ordre de kilomètres et peut croître ou persister sur de longues périodes. Dans le nuage, des tourbillons peuvent se produire sur des échelles de l’ordre du millimètre . Pour des débits plus petits tels que dans les tuyaux, les micro-échelles peuvent être beaucoup plus petites. La majeure partie de l’énergie cinétique de l’écoulement turbulent est contenue dans les structures à grande échelle. L’énergie «passe en cascade» de ces structures à l’échelle macroscopique aux structures à l’échelle microscopique par un mécanisme inertiel. Ce processus est connu sous le nom de cascade d’énergie turbulente .
Les plus petites échelles de l’écoulement turbulent sont connues sous le nom d’ échelles de Kolmogorov . Celles-ci sont suffisamment petites pour que la diffusion moléculaire devienne importante et qu’une dissipation visqueuse de l’énergie ait lieu et que l’énergie cinétique turbulente soit dissipée en chaleur.
Les plus petites échelles en écoulement turbulent, c’est-à-dire les micro- échelles de Kolmogorov sont:
où ε est le taux moyen de dissipation de l’énergie cinétique de turbulence par unité de masse et a des dimensions (m 2 / s 3 ). ν est la viscosité cinématique du fluide et a des dimensions (m 2 / s).
La taille du plus petit tourbillon dans l’écoulement est déterminée par la viscosité. L’ échelle de longueur de Kolmogorov diminue à mesure que la viscosité diminue. Pour les flux à nombre de Reynolds très élevé , les forces visqueuses sont plus faibles par rapport aux forces inertielles. Des mouvements à plus petite échelle sont alors nécessairement générés jusqu’à ce que les effets de la viscosité deviennent importants et que l’énergie soit dissipée. Le rapport des échelles de longueur les plus grandes aux plus petites dans l’écoulement turbulent est proportionnel au nombre de Reynolds (augmente avec la puissance des trois quarts ).
Cela rend pratiquement impossible la simulation numérique directe d’un écoulement turbulent. Par exemple, considérons un flux avec un nombre de Reynolds de 10 6 . Dans ce cas, le rapport L / l est proportionnel à 10 18/4 . Comme nous devons analyser un problème tridimensionnel, nous devons calculer une grille qui comprenait au moins 10 14 points de grille . Cela dépasse de loin la capacité et les possibilités des ordinateurs existants.
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci