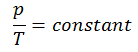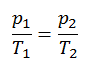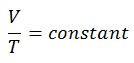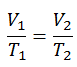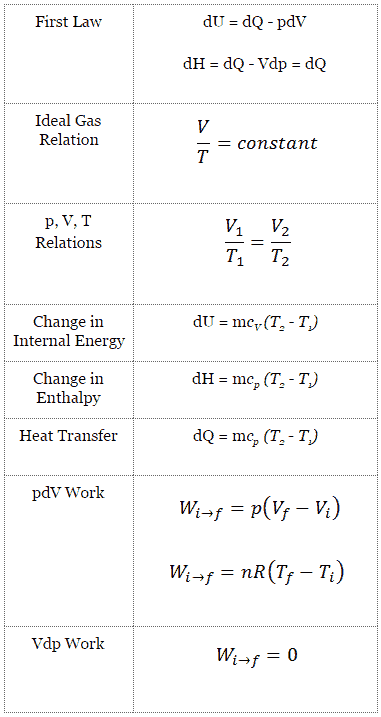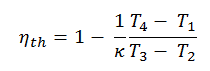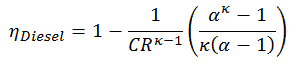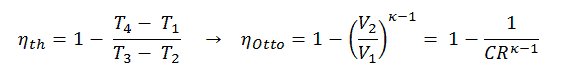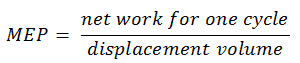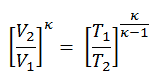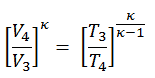Ciclo de Diesel – Motor a Diesel
Na década de 1890, um inventor alemão, Rudolf Diesel patenteou sua invenção de um eficiente, de combustão lenta, ignição por compressão, motor de combustão interna. O ciclo original proposto por Rudolf Diesel era um ciclo de temperatura constante. Nos anos posteriores, Diesel percebeu que seu ciclo original não funcionaria e adotou o ciclo de pressão constante, conhecido como ciclo de Diesel .
O ciclo diesel é um dos ciclos termodinâmicos mais comuns encontrados em motores de automóveis e descreve o funcionamento de um motor de pistão de ignição por compressão típico. O motor Diesel é semelhante em operação ao motor a gasolina. A diferença mais importante é que:
- Não há combustível no cilindro no início do curso de compressão; portanto, uma autoignição não ocorre nos motores a diesel.
- O motor diesel usa ignição por compressão em vez de ignição por faísca.
- Devido à alta temperatura desenvolvida durante a compressão adiabática, o combustível inflama espontaneamente à medida que é injetado. Portanto, não são necessárias velas de ignição.
- Antes do início do curso de força, os injetores começam a injetar combustível diretamente na câmara de combustão e, portanto, a primeira parte do curso de força ocorre aproximadamente à pressão constante.
- Taxas de compressão mais altas podem ser alcançadas em motores a diesel do que em motores Otto
Ao contrário do ciclo Otto , o ciclo Diesel não executa adição de calor isocórico. Em um ciclo Diesel ideal, o sistema que executa o ciclo passa por uma série de quatro processos: dois processos isentrópicos (adiabáticos reversíveis) alternados com um processo isocórico e um processo isobárico.Como o princípio de Carnot afirma que nenhum motor pode ser mais eficiente do que um motor reversível ( um motor a quente Carnot ) operando entre os mesmos reservatórios de alta e baixa temperatura, o motor Diesel deve ter uma eficiência mais baixa que a eficiência de Carnot. Um típico motor automotivo a diesel opera com cerca de 30% a 35% de eficiência térmica. Cerca de 65-70% é rejeitado como calor residual sem ser convertido em trabalho útil, ou seja, trabalho entregue às rodas. Em geral, os motores que usam o ciclo Diesel geralmente são mais eficientes do que os motores que usam o ciclo Otto. O motor diesel tem a mais alta eficiência térmica de qualquer motor de combustão prático. Motores diesel de baixa velocidade(como usado em navios) pode ter uma eficiência térmica superior a 50% . O maior motor diesel do mundo chega a 51,7%.
Ciclo Diesel – Processos
Em um ciclo Diesel ideal, o sistema que executa o ciclo passa por uma série de quatro processos: dois processos isentrópicos (adiabáticos reversíveis) alternados com um processo isocórico e um processo isobárico.
-
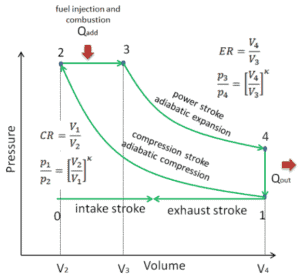
diagrama pV de um ciclo Diesel ideal Compressão isentrópica (curso de compressão) – O ar é comprimido adiabaticamente do estado 1 ao estado 2, conforme o pistão se move do ponto morto inferior para o ponto morto superior. O ambiente trabalha com o gás, aumentando sua energia interna (temperatura) e comprimindo-o. Por outro lado, a entropia permanece inalterada. As mudanças nos volumes e sua proporção ( V 1 / V 2 ) são conhecidas como taxa de compressão.
- Expansão isobárica (fase de ignição) – Nesta fase (entre o estado 2 e o estado 3), há uma transferência de calor de pressão constante (modelo idealizado) para o ar a partir de uma fonte externa (combustão de combustível injetado) enquanto o pistão está se movendo em direção ao V 3 . Durante o processo de pressão constante, a energia entra no sistema à medida que o calor Q é adicionado e uma parte do trabalho é feita movendo o pistão.
- Expansão isentrópica (poder acidente vascular cerebral) – O gás expande-se adiabaticamente de estado 3 para o estado 4, quando o pistão se move da V 3 a centro morto inferior. O gás trabalha nos arredores (pistão) e perde uma quantidade de energia interna igual ao trabalho que sai do sistema. Novamente a entropia permanece inalterada. A taxa de volume ( V 4 / V 3 ) é conhecida como taxa de expansão isentrópica.
- Descompressão isocórica (curso de exaustão) – Nesta fase, o ciclo é concluído por um processo de volume constante no qual o calor é rejeitado do ar enquanto o pistão está no ponto morto inferior. A pressão do gás de trabalho cai instantaneamente do ponto 4 para o ponto 1. A válvula de escape se abre no ponto 4. O curso de escape ocorre imediatamente após esta descompressão. À medida que o pistão se move do ponto morto inferior (ponto 1) para o ponto morto superior (ponto 0) com a válvula de escape aberta, a mistura gasosa é ventilada para a atmosfera e o processo recomeça.
Durante o ciclo diesel, o trabalho é realizado sobre o gás pelo pistão entre os estados 1 e 2 ( i compressão sentropic ). O trabalho é realizado pelo gás no pistão entre os estágios 2 e 3 ( i adição de calor sobárico ) e entre os estágios 2 e 3 ( i expansão sentrópica ). A diferença entre o trabalho realizado pelo gás e o trabalho realizado com o gás é o trabalho líquido produzido pelo ciclo e corresponde à área delimitada pela curva do ciclo. O trabalho produzido pelos tempos de ciclo, a taxa do ciclo (ciclos por segundo) é igual à potência produzida pelo motor Diesel.
Processo isentrópico
Um processo isentrópico é um processo termodinâmico , no qual a entropia do fluido ou gás permanece constante. Isso significa que o processo isentrópico é um caso especial de um processo adiabático no qual não há transferência de calor ou matéria. É um processo adiabático reversível . A suposição de que não há transferência de calor é muito importante, pois podemos usar a aproximação adiabática apenas em processos muito rápidos .
Processo isentrópico e a primeira lei
Para um sistema fechado, podemos escrever a primeira lei da termodinâmica em termos de entalpia :
dH = dQ + Vdp
ou
dH = TdS + Vdp
Processo isentrópico (dQ = 0):
dH = Vdp → W = H 2 – H 1 → H 2 – H 1 = C P (T 2 – T 1 ) (para gás ideal )
Processo isentrópico do gás ideal
O processo isentrópico (um caso especial de processo adiabático) pode ser expresso com a lei dos gases ideais como:
pV κ = constante
ou
p 1 V 1 k = p 2 V 2 k
em que κ = c p / c v é a proporção de aquecimentos específicos (ou capacidades de calor ) para o gás. Um para pressão constante (c p ) e outro para volume constante (c v ) . Observe que essa razão κ = c p / c v é um fator na determinação da velocidade do som em um gás e em outros processos adiabáticos.
Processo Isocórico
Um processo isocórico é um processo termodinâmico, no qual o volume do sistema fechado permanece constante (V = const). Ele descreve o comportamento do gás dentro do recipiente, que não pode ser deformado. Como o volume permanece constante, a transferência de calor para dentro ou para fora do sistema não funciona , mas altera apenas a energia interna (a temperatura) do sistema.
Processo isocórico e a primeira lei
A forma clássica da primeira lei da termodinâmica é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira . Então:
dU = dQ – pdV
No processo isocórico e no gás ideal , todo o calor adicionado ao sistema será usado para aumentar a energia interna.
Processo isocórico (pdV = 0):
dU = dQ (para gás ideal)
dU = 0 = Q – W → W = Q (para gás ideal)
Processo isocórico do gás ideal
O processo isocórico pode ser expresso com a lei dos gases ideais como:
ou
Em um diagrama pV , o processo ocorre ao longo de uma linha horizontal que possui a equação V = constante.
Veja também: Lei de Guy-Lussac
Processo isobárico
Um processo isobárico é um processo termodinâmico , no qual a pressão do sistema permanece constante (p = const). A transferência de calor para dentro ou para fora do sistema funciona, mas também altera a energia interna do sistema.
Como existem mudanças na energia interna (dU) e no volume do sistema (∆V), os engenheiros costumam usar a entalpia do sistema, que é definida como:
H = U + pV
Processo isobárico e a primeira lei
A forma clássica da primeira lei da termodinâmica é a seguinte equação:
dU = dQ – dW
Nesta equação, dW é igual a dW = pdV e é conhecido como trabalho de fronteira . Em um processo isobárico e no gás ideal, parte do calor adicionado ao sistema será usada para realizar o trabalho e parte do calor adicionado aumentará a energia interna (aumentará a temperatura). Portanto, é conveniente usar a entalpia em vez da energia interna.
Processo isobárico (Vdp = 0):
dH = dQ → Q = H 2 – H 1
Na entropia constante , ou seja, no processo isentrópico, a mudança de entalpia é igual ao trabalho do processo de fluxo realizado no sistema ou pelo mesmo.
Processo isobárico do gás ideal
O processo isobárico pode ser expresso com a lei do gás ideal como:
ou
Em um diagrama de pV , o processo ocorre ao longo de uma linha horizontal (chamada isobar) que possui a equação p = constante.
Veja também: Lei de Charles
Ciclo Diesel – pV, diagrama Ts

Os ciclos de diesel são frequentemente plotados em um diagrama pressão-volume (diagrama pV) e em um diagrama temperatura-entropia (diagrama Ts).
Quando plotados em um diagrama de volume de pressão , o processo isobárico segue a linha isobárica do gás (as linhas horizontais), o processo isocórico segue a linha isocórica do gás (a linha vertical), os processos adiabáticos se movem entre essas linhas e a área delimitada pelo caminho completo do ciclo representa o trabalho total que pode ser realizado durante um ciclo.
O diagrama de temperatura-entropia ( diagrama Ts) no qual o estado termodinâmico é especificado por um ponto em um gráfico com entropia (s) específica (s) como eixo horizontal e temperatura absoluta (T) como eixo vertical. Os diagramas Ts são uma ferramenta útil e comum, principalmente porque ajuda a visualizar a transferência de calor durante um processo. Para processos reversíveis (ideais), a área sob a curva Ts de um processo é o calor transferido para o sistema durante esse processo.
Motor Diesel de Quatro Tempos
Os motores a diesel podem ser projetados como ciclos de dois ou quatro tempos. O motor a diesel de quatro tempos é um motor de combustão interna (IC) no qual o pistão executa quatro cursos separados enquanto gira um eixo de manivela. Um curso refere-se ao curso completo do pistão ao longo do cilindro, em qualquer direção. Portanto, cada curso não corresponde ao processo termodinâmico único fornecido no capítulo Ciclo Diesel – Processos.
O motor de quatro tempos compreende:
-
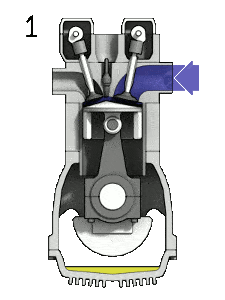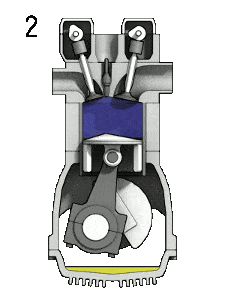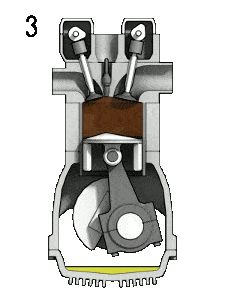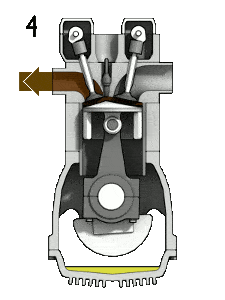
O motor Diesel é semelhante em operação ao motor a gasolina. Nesta foto, existe um mecanismo Otto, que é acionado por uma vela de ignição em vez da própria compressão. Motor a quatro tempos – motor Otto
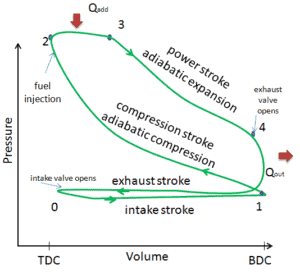
Fonte: wikipedia.org, trabalho próprio da Zephyris, CC BY-SA 3.0o curso de admissão – O pistão se move do ponto morto superior (TDC) para o ponto morto inferior (BDC) e o ciclo passa pelos pontos 0 → 1. Nesse curso, a válvula de admissão está aberta enquanto o pistão aspira ar (sem combustível) cilindro, produzindo pressão de vácuo no cilindro através de seu movimento descendente.
- o curso de compressão – O pistão se move do ponto morto inferior (BDC) para o ponto morto superior (TDC) e o ciclo passa pelos pontos 1 → 2. Neste curso, as válvulas de admissão e exaustão são fechadas, resultando em compressão de ar adiabática (ou seja, sem transferência de calor para ou do ambiente). Durante essa compressão, o volume é reduzido, a pressão e a temperatura aumentam. No final deste curso, o combustível é injetado e queima no ar quente comprimido. No final deste curso, a cambota completou uma revolução completa de 360 graus.
- o curso de força – O pistão se move do ponto morto superior (TDC) para o ponto morto inferior (BDC) e o ciclo passa pelos pontos 2 → 3 → 4. Nesse curso, as válvulas de admissão e de escape estão fechadas. No início do curso de força, ocorre uma combustão quase isobárica entre 2 e 3. Nesse intervalo, a pressão permanece constante desde que o pistão desce e o volume aumenta. Às 3 horas, a injeção e a combustão do combustível estão completas, e o cilindro contém gás a uma temperatura mais alta que a 2. Entre 3 e 4, esse gás quente se expande, novamente aproximadamente adiabaticamente. Nesse curso, o pistão é direcionado para o eixo de manivela, o volume aumenta e o trabalho é realizado pelo gás no pistão.
- o curso de escape. O pistão se move do ponto morto inferior (BDC) para o ponto morto superior (TDC) e o ciclo passa pelos pontos 4 → 1 → 0. Nesse curso, a válvula de escape está aberta enquanto o pistão puxa os gases de escape para fora da câmara. No final deste curso, a cambota completou uma segunda revolução completa de 360 graus.
Observe que: Em um caso ideal, a expansão adiabática deve continuar até que a pressão caia para a do ar circundante. Isso aumentaria a eficiência térmica desse mecanismo, mas também causaria dificuldades práticas com o motor. Simplesmente o motor teria que ser muito maior.
Comparação de ciclos diesel reais e ideais
 Neste artigo, é mostrado um ciclo Diesel ideal, no qual existem muitas suposições diferentes do ciclo Diesel real . As principais diferenças entre o motor Diesel real e ideal aparecem na figura. Na realidade, o ciclo ideal não ocorre e há muitas perdas associadas a cada processo. Para um ciclo real, a forma do diagrama de pV é semelhante ao ideal, mas a área (trabalho) delimitada pelo diagrama de pV é sempre menor que o valor ideal. O ciclo Diesel ideal é baseado nas seguintes premissas:
Neste artigo, é mostrado um ciclo Diesel ideal, no qual existem muitas suposições diferentes do ciclo Diesel real . As principais diferenças entre o motor Diesel real e ideal aparecem na figura. Na realidade, o ciclo ideal não ocorre e há muitas perdas associadas a cada processo. Para um ciclo real, a forma do diagrama de pV é semelhante ao ideal, mas a área (trabalho) delimitada pelo diagrama de pV é sempre menor que o valor ideal. O ciclo Diesel ideal é baseado nas seguintes premissas:
- Ciclo fechado : A maior diferença entre os dois diagramas é a simplificação dos movimentos de admissão e escape no ciclo ideal. No curso de escape, o calor Q out é ejetado para o ambiente (em um motor real, o gás sai do motor e é substituído por uma nova mistura de ar e combustível).
- Adição de calor isobárico . Em motores reais, a adição de calor nunca é isobárica.
- Sem transferência de calor
- Compressão – O gás é comprimido adiabaticamente do estado 1 ao estado 2. Nos motores reais, sempre existem algumas ineficiências que reduzem a eficiência térmica.
- Expansão. O gás se expande adiabaticamente do estado 3 para o estado 4.
- Combustão completa da mistura.
- Nenhum trabalho de bombeamento . Trabalho de bombeamento é a diferença entre o trabalho realizado durante o golpe de escape e o trabalho realizado durante o golpe de admissão. Nos ciclos reais, há uma diferença de pressão entre as pressões de exaustão e de entrada.
- Sem perda de purga . A perda de purga é causada pela abertura precoce das válvulas de escape. Isso resulta em uma perda de produção durante o curso de expansão.
- Sem perda de impacto . A perda soprada é causada pelo vazamento de gases comprimidos através de anéis de pistão e outras fendas.
- Sem perdas por atrito .
Essas suposições e perdas simplificadoras levam ao fato de que a área fechada (trabalho) do diagrama de pV para um motor real é significativamente menor que o tamanho da área (trabalho) envolvida pelo diagrama de pV do ciclo ideal. Em outras palavras, o ciclo ideal do motor superestimará o trabalho líquido e, se os motores funcionarem na mesma velocidade, maior potência produzida pelo motor real em cerca de 20% (da mesma forma que no caso do motor Otto).
Taxa de compressão – Otto Engine
A taxa de compressão , CR , é definida como a taxa do volume no ponto morto inferior e o volume no ponto morto superior. É uma das principais características de muitos motores de combustão interna. Na seção a seguir, será mostrado que a taxa de compressão determina a eficiência térmica do ciclo termodinâmico usado do motor de combustão. Em geral, é desejável ter uma alta taxa de compressão, pois permite que um motor atinja maior eficiência térmica.
Por exemplo, vamos supor um ciclo Otto com taxa de compressão de CR = 10: 1. O volume da câmara é de 500 cm = 500 x 10 -6 m 3 (0,5 L) antes do curso de compressão. Para este motor um ll necessário volumes são conhecidos:
- V 1 = V 4 = V max = 500 × 10 -6 m 3 (0,5l)
- V 2 = V 3 = V min = V máx / CR = 55,56 × 10 -6 m 3
Observe que (V max – V min ) x número de cilindros = cilindrada total do motor.
Exemplos de taxas de compressão – Gasolina x Diesel
- A taxa de compactação em um motor a gasolina geralmente não será muito maior que 10: 1 devido a uma possível batida no motor (autoignição) e não menor que 6: 1 .
- Um Subaru Impreza WRX turbo tem uma taxa de compressão de 8,0: 1 . Em geral, os motores turboalimentados ou sobrealimentados já possuem ar comprimido na entrada de ar, portanto são geralmente construídos com menor taxa de compressão.
- Um motor Honda S2000 (F22C1) tem uma taxa de compressão de 11,1: 1 .
- Alguns motores de carros esportivos atmosféricos podem ter uma taxa de compressão de até 12,5: 1 (por exemplo, Ferrari 458 Italia).
- Em 2012, a Mazda lançou novos motores a gasolina sob a marca SkyActiv com uma taxa de compressão de 14: 1 . Para reduzir o risco de bater no motor, o gás residual é reduzido usando sistemas de escape do motor 4-2-1 , implementando uma cavidade do pistão e otimizando a injeção de combustível.
- Os motores a diesel têm uma taxa de compressão que normalmente excede 14: 1 e taxas acima de 22: 1 também são comuns.
Eficiência térmica para ciclo diesel
Em geral, a eficiência térmica , η th , de qualquer motor de calor é definida como a razão entre o trabalho que faz, W , para o calor de entrada a uma temperatura elevada, Q H .
A eficiência térmica , η th , representa a fração de calor , Q H , que é convertida em trabalho . Como a energia é conservada de acordo com a primeira lei da termodinâmica e a energia não pode ser convertida para funcionar completamente, a entrada de calor, Q H , deve ser igual ao trabalho realizado, W, mais o calor que deve ser dissipado como calor residual Q C no meio Ambiente. Portanto, podemos reescrever a fórmula da eficiência térmica como:
O calor absorvido ocorre durante a combustão da mistura combustível-ar, quando a faísca ocorre, aproximadamente a volume constante. Como durante um processo isocórico não há trabalho realizado pelo sistema ou sobre ele, a primeira lei da termodinâmica determina ∆U = ∆Q. Portanto, o calor adicionado e rejeitado é dado por:
Q add = mc p (T 3 – T 2 )
Q out = mc v (T 4 – T 1 )
Substituindo essas expressões pelo calor adicionado e rejeitado na expressão por eficiência térmica, obtém-se:
Essa equação pode ser reorganizada na forma com a taxa de compressão e a taxa de corte:
Onde
- η Diesel é a eficiência térmica máxima de um ciclo Diesel
- α é a razão de corte V 3 / V 2 (ou seja, a razão de volumes no final e no início da fase de combustão)
- CR é a taxa de compressão
- κ = c p / c v = 1,4
É uma conclusão muito útil, pois é desejável alcançar uma alta taxa de compressão para extrair mais energia mecânica de uma determinada massa do combustível. Como concluímos na seção anterior, a eficiência térmica do ciclo Otto padrão do ar também é uma função da taxa de compressão e κ.
Quando as comparamos com as fórmulas, pode-se observar que, para uma determinada taxa de compressão (CR), o ciclo Otto será mais eficiente que o ciclo Diesel. Mas os motores a diesel geralmente são mais eficientes, pois são capazes de operar com taxas de compressão mais altas.
Nos motores Otto comuns, a taxa de compressão tem seus limites. A taxa de compressão em um motor a gasolina geralmente não será muito superior a 10: 1. Taxas de compressão mais altas sujeitarão os motores a gasolina a bater no motor, causados pela autoignição de uma mistura não queimada, se for usado combustível com classificação mais baixa de octanagem. Nos motores a diesel, há um risco mínimo de autoignição do combustível, porque os motores a diesel são motores de ignição por compressão e não há combustível no cilindro no início do curso de compressão.
Pressão Efetiva Média – MEP
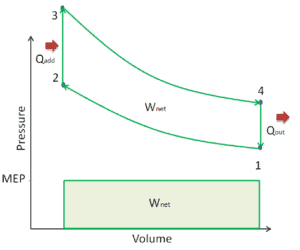
Um parâmetro usado pelos engenheiros para descrever o desempenho dos motores de pistão alternativo é conhecido como pressão efetiva média , ou MEP . O MEP é uma medida muito útil da capacidade de um motor para executar um trabalho independente do deslocamento do motor. Existem vários tipos de MEP. Esses MEPs são definidos pela medição da localização e pelo método de cálculo (por exemplo, BMEP ou IMEP).
Em geral, a pressão efetiva média é a pressão constante teórica que, se ela atuasse no pistão durante o curso de força, produziria o mesmo trabalho líquido como realmente desenvolvido em um ciclo completo. O MEP pode ser definido como:
Por exemplo, a pressão efetiva média líquida indicada , conhecida como IMEP n é igual à pressão efetiva média calculada a partir da pressão no cilindro (deve haver essa medição) durante todo o ciclo do motor. Observe que é 720 ° para um motor a quatro tempos e 360 ° para um motor a dois tempos.
Alguns exemplos:
- O MEP de um motor a gasolina atmosférico pode variar de 8 a 11 bar na região de torque máximo.
- O MEP de um motor a gasolina turbo pode variar de 12 a 17 bar.
- O MEP de um motor diesel atmosférico pode variar de 7 a 9 bar.
- MEP de um motor diesel turboalimentado pode variar de 14 a 18 bar
Por exemplo, um motor a gasolina a quatro tempos produzindo 200 N · m a partir de 2 litros de deslocamento possui um MPE de (4π) (200 N · m) / (0,002 m³) = 1256000 Pa = 12 bar. Como pode ser visto, o MEP é uma característica útil de um motor . Para dois motores de igual volume de cilindrada, aquele com um MEP maior produziria o maior trabalho líquido e, se os motores funcionassem na mesma velocidade, maior potência .
Ciclo Diesel – Problema com a Solução

Vamos assumir o ciclo Diesel, que é um dos ciclos termodinâmicos mais comuns encontrados em motores de automóveis . Um dos principais parâmetros desses motores é a mudança de volumes entre o ponto morto superior (TDC) e o ponto morto inferior (BDC). A proporção desses volumes ( V 1 / V 2 ) é conhecida como taxa de compressão . Também a relação de corte V 3 / V 2 , que é a relação dos volumes no final e no início da fase de combustão.
Neste exemplo, vamos assumir o ciclo Diesel com taxa de compressão de CR = 20: 1 e taxa de corte α = 2. O ar está a 100 kPa = 1 bar, 20 ° C (293 K) e o volume da câmara é de 500 cm³ antes do curso de compressão.
- Capacidade térmica específica a pressão constante do ar à pressão atmosférica e à temperatura ambiente: c p = 1,01 kJ / kgK.
- Capacidade térmica específica a um volume constante de ar à pressão atmosférica e à temperatura ambiente: c v = 0,718 kJ / kgK.
- κ = c p / c v = 1,4
Calcular:
- a massa de entrada de ar
- a temperatura T 2
- a pressão p 2
- a temperatura T 3
- a quantidade de calor adicionada pela queima da mistura combustível-ar
- a eficiência térmica deste ciclo
- o deputado
Solução:
1)
No início dos cálculos, temos que determinar a quantidade de gás no cilindro antes do curso de compressão. Usando a lei do gás ideal, podemos encontrar a massa:
pV = mR específico T
Onde:
- p é a pressão absoluta do gás
- m é a massa da substância
- T é a temperatura absoluta
- V é o volume
- R específico é a constante de gás específica, igual à constante de gás universal dividida pela massa molar (M) do gás ou mistura. Para ar seco R específico = 287,1 J.kg -1 .K -1 .
Portanto
m = p 1 V 1 / R específico T 1 = (100000 × 500 × 10 -6 ) / (287,1 × 293) = 5,95 × 10 -4 kg
2)
Nesse problema, todos os volumes são conhecidos:
- V 1 = V 4 = V max = 500 × 10 -6 m 3 (0,5l)
- V 2 = V min = V máx / CR = 25 × 10 -6 m 3
Observe que (V max – V min ) x número de cilindros = cilindrada total do motor
Como o processo é adiabático, podemos usar a seguinte relação p, V, T para processos adiabáticos:
portanto
T 2 = T 1 . CR k – 1 = 293. 20 0,4 = 971 K
3)
Novamente, podemos usar a lei do gás ideal para encontrar a pressão no final do curso de compressão como:
P 2 = mR específico T 2 / V 2 = 5,95 x 10 -4 x 287,1 x 971/25 x 10 -6 = 6.635.000 Pa = 66,35 barra
4)
Como o processo 2 → 3 ocorre a pressão constante, a equação ideal de estado do gás fornece
T 3 = (V 3 / V 2 ) x T 2 = 1942 K
Para calcular a quantidade de calor adicionada pela queima da mistura combustível-ar, adicione Q , precisamos usar a primeira lei da termodinâmica para o processo isobárico, que afirma:
Q add = mc p (T 3 – T 2 ) = 5,95 x 10 -4 x 1010 x 971 = 583,5 J
5)
Eficiência térmica para este ciclo Diesel:
Como foi derivado na seção anterior, a eficiência térmica do ciclo Diesel é uma função da taxa de compressão, da taxa de corte e κ:
- η Diesel é a eficiência térmica máxima de um ciclo Diesel
- α é a razão de corte V 3 / V 2 (ou seja, a razão de volumes no final e no início da fase de combustão)
- CR é a taxa de compressão
- κ = c p / c v = 1,4
Para este exemplo:
η Diesel = 0,6467 = 64,7%
6)
O MEP foi definido como:
Nesta equação, o volume de deslocamento é igual a V max – V min . O trabalho líquido para um ciclo pode ser calculado usando o calor adicionado e a eficiência térmica:
W net = Q add . η Otto = 583,5 x 0,6467 = 377,3 J
MEP = 377,3 / ( 500 × 10 -6 – 25 × 10 -6 ) = 794,3 kPa = 7,943 bar
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.