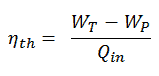O que é exemplo de ciclo de Rankine – problema com solução – definição

Exemplo de ciclo Rankine – problema com solução

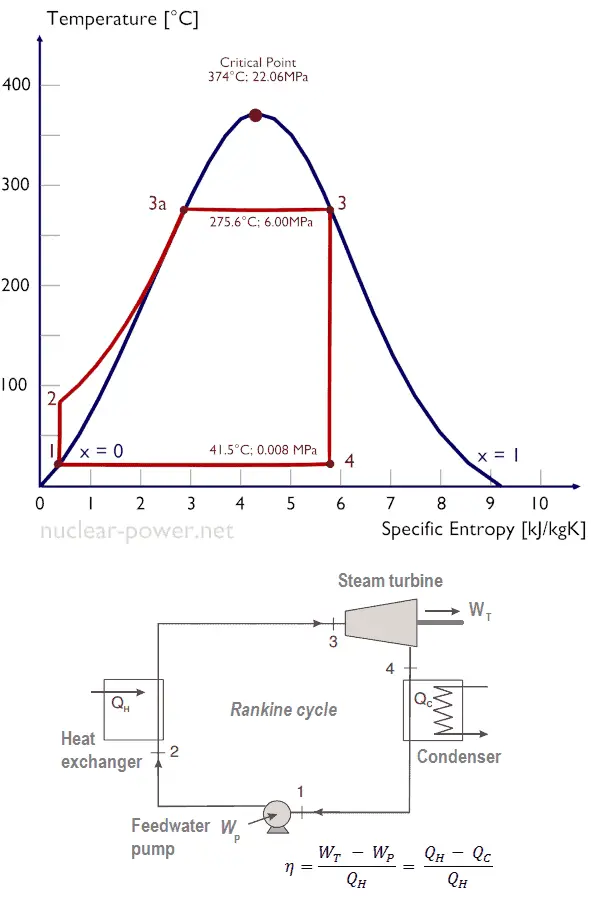Vamos assumir o ciclo Rankine , que é um dos ciclos termodinâmicos mais comuns em usinas termelétricas. Nesse caso, assuma um ciclo simples, sem reaquecimento e sem a turbina a vapor de condensação funcionando com vapor saturado  (vapor seco). Nesse caso, a turbina opera em estado estacionário com condições de entrada de 6 MPa, t = 275,6 ° C, x = 1 (ponto 3). O vapor sai deste estágio da turbina a uma pressão de 0,008 MPa, 41,5 ° C e x = ??? (ponto 4)

Calcular:

1. a qualidade do vapor do vapor de saída
2. a diferença de entalpia entre estes dois estados (3 → 4), a qual corresponde ao trabalho realizado pelo vapor, W _t .
3. a diferença de entalpia entre estes dois estados (1 → 2), que corresponde ao trabalho feito por bombas, W _P .
4. a diferença de entalpia entre esses dois estados (2 → 3), que corresponde ao calor líquido adicionado no gerador de vapor
5. a eficiência termodinâmica deste ciclo e compare esse valor com a eficiência de Carnot

1)

Como não sabemos a qualidade exata do vapor de saída, precisamos determinar esse parâmetro. O estado 4 é fixado pela pressão p ₄ = 0,008 MPa e o fato de que a entropia específica é constante para a expansão isentrópica (s ₃ = s ₄ = 5,89 kJ / kgK para 6 MPa ). A entropia específica de água líquida saturada (x = 0) e vapor seco (x = 1) pode ser escolhida nas tabelas de vapor . No caso de vapor úmido, a entropia real pode ser calculada com a qualidade do vapor, x, e as entropias específicas de água líquida saturada e vapor seco:

s ₄ = s _v x + (1 – x) s _l

Onde

s ₄ = entropia de vapor úmido (J / kg K) = 5,89 kJ / kgK

s _v = entropia do vapor “seco” (J / kg K) = 8,227 kJ / kgK (para 0,008 MPa)

s _l = entropia de água líquida saturada (J / kg K) = 0,592 kJ / kgK (para 0,008 MPa)

A partir desta equação, a qualidade do vapor é:

x ₄ = ( s ₄ – s _l ) / ( s _v – s _l ) = (5,89 – 0,592) / (8,227 – 0,592) = 0,694 = 69,4%

2)

A entalpia para o estado 3 pode ser coletada diretamente das tabelas de vapor, enquanto a entalpia para o estado 4 deve ser calculada usando a qualidade do vapor:

h _{3, v} = 2785 kJ / kg

h _{4, molhado} = h _{4, v} x + (1 – x) h _{4, l}  = 2576. 0,694 + (1 – 0,694). 174 = 1787 + 53,2 = 1840 kJ / kg

Então o trabalho realizado pelo vapor, W _T, é

W _T = Δh = 945 kJ / kg

3)

A entalpia para o estado 1 pode ser obtida diretamente das tabelas de vapor:

h _{1, l} = 174 kJ / kg

O estado 2 é fixado pela pressão p ₂ = 6,0 MPa e pelo fato de a entropia específica ser constante para a compressão isentrópica (s ₁ = s ₂ = 0,592 kJ / kgK para 0,008 MPa ). Para esta entropia s ₂ = 0,592 kJ / kgK ep ₂ = 6,0 MPa, encontramos h _{2, sub-resfriado} em tabelas de vapor para água comprimida (usando interpolação entre dois estados).

h _{2, sub-resfriado} = 179,7 kJ / kg

Então, o trabalho realizado pelas bombas, W _P, é

W _P = Δh = 5,7 kJ / kg

4)

A diferença de entalpia entre (2 → 3), que corresponde ao calor líquido adicionado no gerador de vapor, é simplesmente:

Q _add = h _{3, v}  – h _{2, sub-resfriado} = 2785 – 179,7 =   2605,3 kJ / kg

Observe que, não há regeneração de calor neste ciclo. Por outro lado, a maior parte do calor adicionado é para a entalpia da vaporização (isto é, para a mudança de fase).

5)

Nesse caso, geradores de vapor, turbinas a vapor, condensadores e bombas de água de alimentação constituem um motor térmico, sujeito às limitações de eficiência impostas pela segunda lei da termodinâmica . No caso ideal (sem atrito, processos reversíveis, design perfeito), este motor térmico teria uma eficiência de Carnot de

η _Carnot = 1 – T _frio / T _quente = 1 – 315/549 = 42,6%

onde a temperatura do reservatório quente é de 275,6 ° C (548,7 K), a temperatura do reservatório frio é de 41,5 ° C (314,7 K).

A eficiência termodinâmica deste ciclo pode ser calculada pela seguinte fórmula:

assim
η _th = (945 – 5,7) / 2605,3 = 0,361 = 36,1%