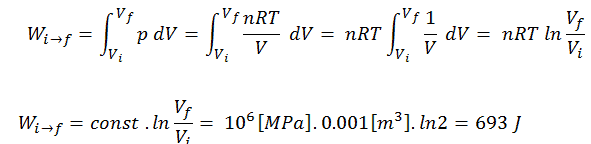Isothermal Process
An isothermal process is a thermodynamic process, in which the temperature of the system remains constant (T = const). The heat transfer into or out of the system typically must happen at such a slow rate in order to continually adjust to the temperature of the reservoir through heat exchange. In each of these states the thermal equilibrium is maintained.
For an ideal gas and a polytropic process, the case n = 1 corresponds to an isothermal (constant-temperature) process. In contrast to adiabatic process , in which n = κ and a system exchanges no heat with its surroundings (Q = 0; ∆T≠0), in an isothermal process there is no change in the internal energy (due to ∆T=0) and therefore ΔU = 0 (for ideal gases) and Q ≠ 0. An adiabatic process is not necessarily an isothermal process, nor is an isothermal process necessarily adiabatic.
In engineering, phase changes, such as evaporation or melting, are isothermal processes when, as is usually the case, they occur at constant pressure and temperature.
Isothermal Process and the First Law
The classical form of the first law of thermodynamics is the following equation:
dU = dQ – dW
In this equation dW is equal to dW = pdV and is known as the boundary work.
In isothermal process and the ideal gas, all heat added to the system will be used to do work:
Isothermal process (dU = 0):
dU = 0 = Q – W → W = Q (for ideal gas)
Isothermal Expansion – Isothermal Compression
See also: What is an Ideal Gas
In an ideal gas, molecules have no volume and do not interact. According to the ideal gas law, pressure varies linearly with temperature and quantity, and inversely with volume.
pV = nRT
where:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation the symbol R is a constant called the universal gas constant that has the same value for all gases—namely, R = 8.31 J/mol K.
The isothermal process can be expressed with the ideal gas law as:
pV = constant
or
p1V1 = p2V2
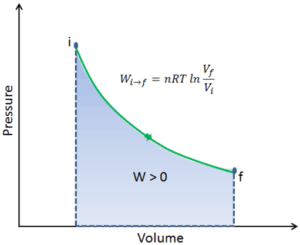
On a p-V diagram, the process occurs along a line (called an isotherm) that has the equation p = constant / V.
Boyle–Mariotte Law
Boyle-Mariotte Law is one of the gas laws. At the end of the 17th century, Robert William Boyle and Edme Mariotte independently studied the relationship between the volume and pressure of a gas at constant temperature. The results of certain experiments with gases at relatively low pressure led Robert Boyle to formulate a well-known law. It states that:
For a fixed mass of gas at constant temperature, the volume is inversely proportional to the pressure.
That means that, for example, if you increase the volume 10 times, the pressure will decrease 10 times. If you halve the volume, you will double the pressure.
You can express this mathematically as:
pV = constant
or
p1V1 = p2V2
Yes, it seems to be identical as isothermal process of ideal gas. In fact, during their experiments the temperature remain constant as was assumed by Mariotte. These results are fully consistent with ideal gas law, which determinates, that the constant is equal to nRT.
pV = nRT
where:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation the symbol R is a constant called the universal gas constant that has the same value for all gases—namely, R = 8.31 J/mol K.
Example of Isothermal Process
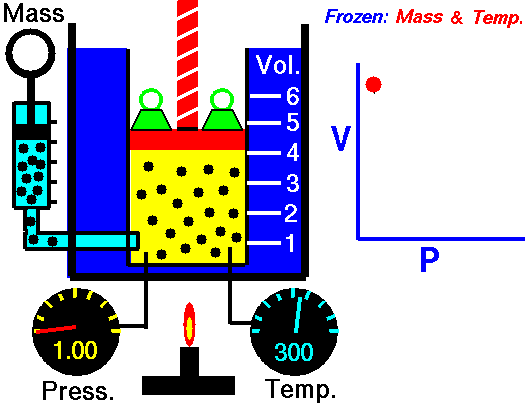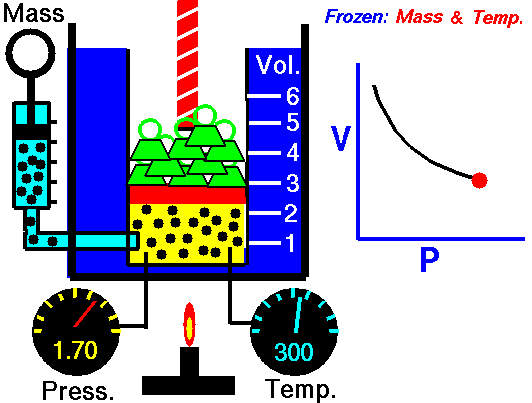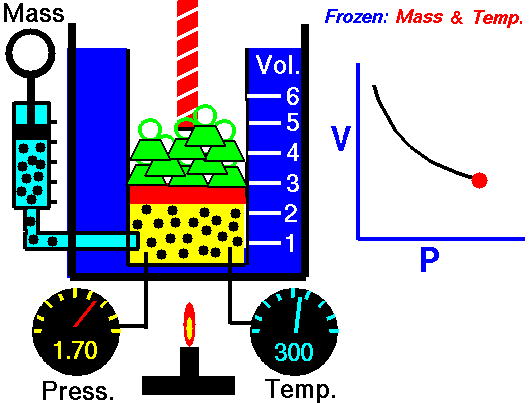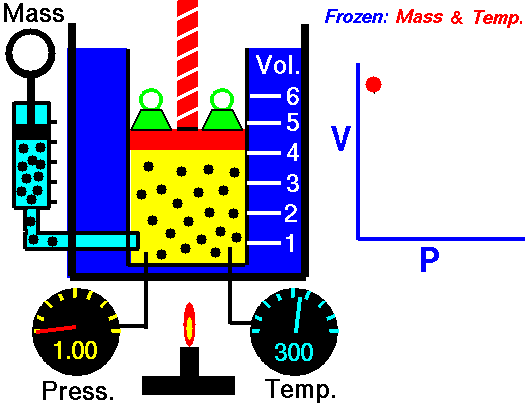
Assume an isothermal expansion of helium (i → f) in a frictionless piston (closed system). The gas expansion is propelled by absorption of heat energy Qadd. The gas expands from initial volume of 0.001 m3 and simultaneously the external load of the piston slowly and continuously decreases from 1 MPa to 0.5 MPa. Since helium behaves almost as an ideal gas, use the ideal gas law to calculate final volume of the chamber and then calculate the work done by the system, when the temperature of the gas is equal to 400 K.
Solution:
The final volume of the gas, Vf, can be calculated using p, V, T Relation for isothermal process:
piVi = pfVf ⇒ Vf = piVi / pf = 2 x 0.001 m3 = 0.002 m3
To calculate such processes, we would need to know how pressure varies with volume for the actual process by which the system changes from state i to state f. Since during this process the internal pressure was not constant, the p∆V work done by the piston must be calculated using the following integral:
By convention, a positive value for work indicates that work is done by the system on its surroundings. A negative value indicates that work is done on the system by its surroundings. The pΔV work is equal to the area under the process curve plotted on the pressure-volume diagram.
Free Expansion – Joule Expansion
These are adiabatic processes in which no transfer of heat occurs between the system and its environment and no work is done on or by the system. These types of adiabatic processes are called free expansion. It is an irreversible process in which a gas expands into an insulated evacuated chamber. It is also called Joule expansion. For an ideal gas, the temperature doesn’t change (this means that the process is also isothermal), however, real gases experience a temperature change during free expansion. In free expansion Q = W = 0, and the first law requires that:
dEint = 0
A free expansion can not be plotted on a P-V diagram, because the process is rapid, not quasistatic. The intermediate states are not equilibrium states, and hence the pressure is not clearly defined.
We hope, this article, Isothermal Process, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.
