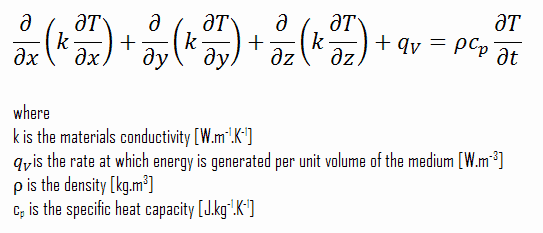What is Interface Boundary Condition – Definition

Interface Boundary Condition

In heat transfer problems, the interface boundary condition can be used when the material is made up of layers of different materials. Solution of a heat transfer problem in such a medium requires the solution of the heat transfer problem in each layer and one must specify an interface condition at each interface. The interface boundary conditions at an interface are based on the two following requirements:

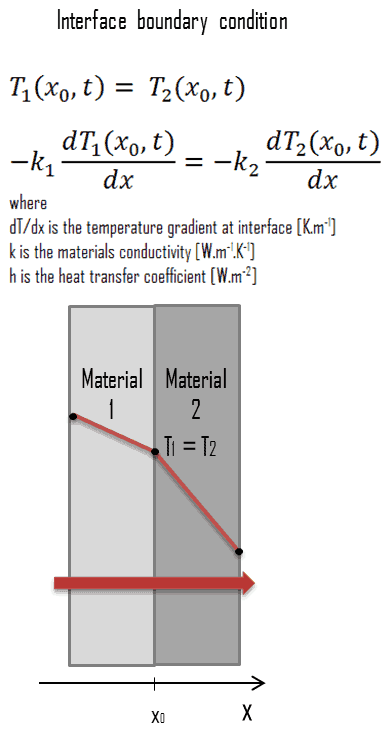
• two bodies in contact must have the same temperature at the area of contact (i.e. an ideal contact without contact resistance)
• an interface cannot store any energy, and therefore the heat conduction at the surface of the first material is equal to the heat conduction at the surface of the second material

Noteworthy, when components are bolted or otherwise pressed together, a knowledge of the thermal performance of such joints are also needed. In these composite systems, the temperature drop across the interface between materials may be appreciable. This temperature drop is characterized by the thermal contact conductance coefficient, h_c, which is a property indicating the thermal conductivity, or ability to conduct heat, between two bodies in contact.

The interface boundary condition can be mathematically expressed in the way depicted in the figure.

General Heat Conduction Equation

The heat conduction equation is a partial differential equation that describes the distribution of heat (or the temperature field) in a given body over time. Detailed knowledge of the temperature field is very important in thermal conduction through materials. Once this temperature distribution is known, the conduction heat flux at any point in the material or on its surface may be computed from Fourier’s law.

The heat equation is derived from Fourier’s law and conservation of energy. The Fourier’s law states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area, at right angles to that gradient, through which the heat flows.

A change in internal energy per unit volume in the material, ΔQ, is proportional to the change in temperature, Δu. That is:

∆Q = ρ.c_p.∆T

General Form

Using these two equation we can derive the general heat conduction equation:

This equation is also known as the Fourier-Biot equation, and provides the basic tool for heat conduction analysis. From its solution, we can obtain the temperature field as a function of time.

In words, the heat conduction equation states that:

At any point in the medium the net rate of energy transfer by conduction into a unit volume plus the volumetric rate of thermal energy generation must equal the rate of change of thermal energy stored within the volume.

See also:

Heat Equation