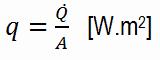Introduction to Heat Transfer
 While internal energy refers to the total energy of all the molecules within the object, heat is the amount of energy flowing from one body to another spontaneously due to their temperature difference. Heat is a form of energy, but it is energy in transit. Heat is not a property of a system. However, the transfer of energy as heat occurs at the molecular level as a result of a temperature difference.
While internal energy refers to the total energy of all the molecules within the object, heat is the amount of energy flowing from one body to another spontaneously due to their temperature difference. Heat is a form of energy, but it is energy in transit. Heat is not a property of a system. However, the transfer of energy as heat occurs at the molecular level as a result of a temperature difference.
Consider a block of metal at high temperature, that consists of atoms that are oscillating intensely around their average positions. At low temperatures, the atoms continue to oscillate, but with less intensity. If a hotter block of metal is put in contact with a cooler block, the intensely oscillating atoms at the edge of the hotter block gives off its kinetic energy to the less oscillating atoms at the edge of the cool block. In this case there is energy transfer between these two blocks and heat flows from the hotter to the cooler block by this random vibrations.
As with work, the amount of heat transferred depends upon the path and not simply on the initial and final conditions of the system. There are actually many ways to take the gas from state i to state f.
Also, as with work, it is important to distinguish between heat added to a system from its surroundings and heat removed from a system to its surroundings. Q is positive for heat added to the system, so if heat leaves the system, Q is negative. Because W in the equation is the work done by the system, then if work is done on the system, W will be negative and Eint will increase.
The symbol q is sometimes used to indicate the heat added to or removed from a system per unit mass. It equals the total heat (Q) added or removed divided by the mass (m).
Distinguishing Temperature, Heat, and Internal Energy
Using the kinetic theory, a clear distinction between these three properties can be made.
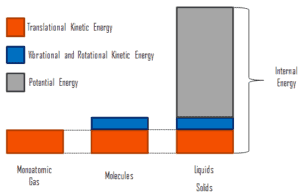
- Temperature is related to the kinetic energies of the molecules of a material. It is the average kinetic energy of individual molecules.
- Internal energy refers to the total energy of all the molecules within the object. It is an extensive property, therefore when two equal-mass hot ingots of steel may have the same temperature, but two of them have twice as much internal energy as one does.
- Finally, heat is the amount of energy flowing from one body to another spontaneously due to their temperature difference.
It must be added, when a temperature difference does exist heat flows spontaneously from the warmer system to the colder system. Thus, if a 5 kg cube of steel at 100°C is placed in contact with a 500 kg cube of steel at 20°C, heat flows from the cube at 300°C to the cube at 20°C even though the internal energy of the 20°C cube is much greater because there is so much more of it.
A particularly important concept is thermodynamic equilibrium. In general, when two objects are brought into thermal contact, heat will flow between them until they come into equilibrium with each other.
Heat Flux Density – Thermal Flux
The rate of heat transfer per unit area normal to the direction of heat transfer is called heat flux. Sometimes it is also referred to as heat flux density. In SI its units are watts per square metre (W.m−2). It has both a direction and a magnitude, and so it is a vector quantity. The average heat flux is expressed as:
where A is the heat transfer area. The unit of heat flux in English units is Btu/h·ft2. Note that heat flux may vary with time as well as position on a surface.
In nuclear reactors, limitations of the local heat flux is of the highest importance for reactor safety. Since nuclear fuel consist of fuel rods, the heat flux is there defined in units of W/cm (local linear heat flux density) or kW/rod (power per fuel rod).
See also: Heat Flux Density
We hope, this article, Introduction to Heat Transfer, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.