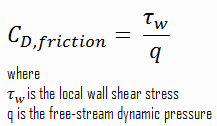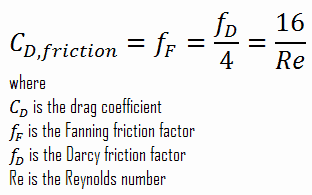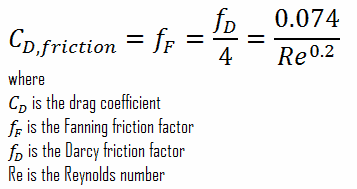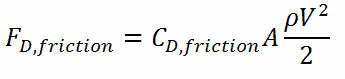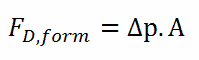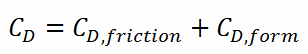What is Parasitic Drag – Definition

What is Parasitic Drag

The term parasitic drag is mainly used in aerodynamics, since for lifting wings drag it is in general small compared to lift. Parasitic drag is a combination of form drag, skin friction drag and interference drag.

Skin Friction – Friction Drag

As was written, a moving fluid exerts tangential shear forces on the surface because of the no-slip condition caused by viscous effects. This type of drag force, depends especially on the geometry, the roughness of the solid surface (only in turbulent flow) and on the type of fluid flow. The friction drag is proportional to the surface area. Therefore, bodies with a larger surface area will experience a larger friction drag. This is why commercial airplanes reduce their total surface area to save fuel. Friction drag is a strong function of viscosity, and an “idealized” fluid with zero viscosity would produce zero friction drag since the wall shear stress would be zero.

Skin friction is caused by viscous drag in the boundary layer around the object. Basic characteristics of all laminar and turbulent boundary layers are shown in the developing flow over a flat plate. The stages of the formation of the boundary layer are shown in the figure below:

There are two ways to decrease friction drag:

• the first is to shape the moving body so that laminar flow is possible
• the second method is to increase the length and decrease the cross-section of the moving object as much as practicable.

The skin friction coefficient, C_D,friction, is defined by

It must be noted, the skin friction coefficient is equal to the Fanning friction factor. The Fanning friction factor, named after John Thomas Fanning, is a dimensionless number, that is one-fourth of the Darcy friction factor. As can be seen, there is a connection between skin friction forces and frictional head losses.

See also: Darcy Friction Factor

For laminar flow in a pipe, the Fanning friction factor (skin friction coefficient) is a consequence of Poiseuille’s law that and it is given by following equations:

In turbulent flows, however, things are more difficult, as the friction factor depends strongly on the pipe roughness. The friction factor for fluid flow can be determined using a Moody chart. For example:

The frictional component of the drag force is given by:

Form Drag – Pressure Drag

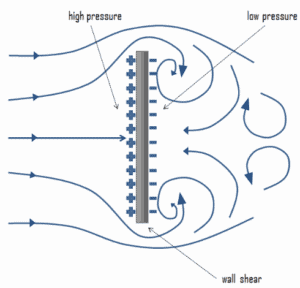Form drag known also as pressure drag arises because of the shape and size of the object. The pressure drag is proportional to the difference between the pressures acting on the front and back of the immersed body, and the frontal area. This type of drag force is also an interesting consequence the Bernoulli’s effect. According to Bernoulli’s principle, faster moving air exerts less pressure. This causes, that there can be a pressure difference between surfaces of the object. The general size and shape of the body are the most important factors in form drag. In general, bodies with a larger presented geometric cross-section will have a higher drag than thinner bodies.

As can be seen from the figure, the drag force arises from the difference between the pressures acting on the front and back of the immersed body. For this force can be calculated (for this case) simply using the definition of pressure as:

Since the head loss is roughly proportional to the square of the flow rate in most engineering flows, the total drag coefficient can be determined by simply adding the friction and pressure drag coefficients:

See also:

Drag