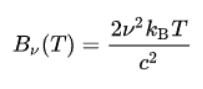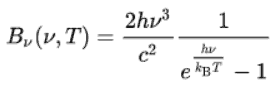What is Ultraviolet Catastrophe – Rayleigh-Jeans Catastrophe – Definition

Ultraviolet Catastrophe

Before the Planck’s hypothesis, physicists tried to describe spectral radiance of electromagnetic radiation by classical physics. The approximation based on classical physsics is known as the Rayleigh-Jeans law.

Similarly as for the Planck’s law, the Rayleigh-Jeans law gives the spectral radiance of a body as a function of frequency ν at absolute temperature T:

where

• B_ν(v,T) is the spectral radiance (the power per unit solid angle and per unit of area normal to the propagation) density of frequency ν radiation per unit frequency at thermal equilibrium at temperature T
• c is the speed of light in a vacuum
• k_B is the Boltzmann constant
• ν is the frequency of the electromagnetic radiation
• T is the absolute temperature of the body

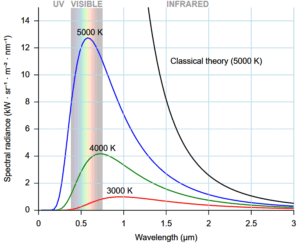
Electromagnetic spectrum predicted by this formula agrees with experimental results at low frequencies (large wavelengths) but strongly disagrees at high frequencies (short wavelengths). This inconsistency between observations and the predictions of classical physics is commonly known as the ultraviolet catastrophe or Rayleigh–Jeans catastrophe. By calculating the total amount of radiant energy (i.e., the sum of emissions in all frequency ranges), it can be shown that a blackbody in this case would release an infinite amount of energy, which is in contradiction with the law of conservation of energy.

The study of the laws of blackbodies and the failure of classical physics to describe them helped establish the foundations of quantum mechanics. Solution of this problem was proposed by a German theoretical physicist Max Planck, who introduced very strange assumption (for the time), that energy is radiated and absorbed in discrete “quanta” (or energy packets). Planck’s assumptions led to the correct form of the spectral distribution functions:

where

• B_ν(v,T) is the spectral radiance (the power per unit solid angle and per unit of area normal to the propagation) density of frequency ν radiation per unit frequency at thermal equilibrium at temperature T
• h is the Planck constant
• c is the speed of light in a vacuum
• k_B is the Boltzmann constant
• ν is the frequency of the electromagnetic radiation
• T is the absolute temperature of the body

Albert Einstein solved the problem by postulating that Planck’s quanta were real physical particles, what we now call photons, not just a mathematical fiction.

Blackbody Radiation

It is known that the amount of radiation energy emitted from a surface at a given wavelength depends on the material of the body and the condition of its surface as well as the surface temperature. Therefore, various materials emit different amounts of radiant energy even whhen they are at the same temperature. A body that emits the maximum amount of heat for its absolute temperature is called a blackbody.

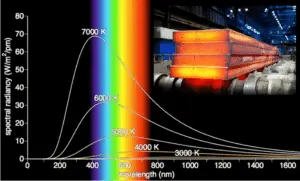A blackbody is an idealized physical body, that has specific properties. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body. They radiate less heat than a black body and therefore are called gray bodies.

The surface of a blackbody emits thermal radiation at the rate of approximately 448 watts per square metre at room temperature (25 °C, 298.15 K). Real objects with emissivities less than 1.0 (e.g. copper wire) emit radiation at correspondingly lower rates (e.g. 448 x 0.03 = 13.4 W/m²). Emissivity plays important role in heat transfer problems. For example, solar heat collectors incorporate selective surfaces that have very low emissivities. These collectors waste very little of the solar energy through emission of thermal radiation.

Since the absorptivity and the emissivity are interconnected by the Kirchhoff’s Law of thermal radiation, a blackbody is also a perfect absorber of electromagnetic radiation.

Kirchhoff’s Law of thermal radiation:

For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.

emissivity ε = absorptivity α

A blackbody absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. Its absorptivity is therefore equal to unity, which is also the highest possible value. That is, a blackbody is a perfect absorber (and a perfect emitter).

Note that visible radiation occupies a very narrow band of the spectrum from 400 to 760 nm, we cannot make any judgments about the blackness of a surface on the basis of visual observations. For example, consider white paper that reflects visible light and thus appear white. On the other hand it is essentially black for infrared radiation (absorptivity α = 0.94) since they strongly absorb long-wavelength radiation.

See also:

Radiation