Erhaltung der Masse
Dieses Prinzip ist allgemein als Prinzip der Erhaltung der Materie bekannt und besagt, dass sich die Masse eines Objekts oder eine Sammlung von Objekten im Laufe der Zeit nie ändert, unabhängig davon, wie sich die Bestandteile neu anordnen. Dieses Prinzip kann bei der Analyse von fließenden Flüssigkeiten angewendet werden . Die Erhaltung der Masse in der Fluiddynamik besagt, dass alle Massenströme in ein Steuervolumen gleich allen Massenströmen außerhalb des Steuervolumens zuzüglich der Änderungsrate der Masse innerhalb des Steuervolumens sind. Dieses Prinzip wird mathematisch durch folgende Gleichung ausgedrückt:
ṁ in = ṁ out + ∆m ⁄ ⁄t
Masseeintrag pro Zeiteinheit = Masseaustritt pro Zeiteinheit + Zunahme der Masse im Kontrollvolumen pro Zeiteinheit

Diese Gleichung beschreibt den Fluss im instationären Zustand . Der Fluss im instationären Zustand bezieht sich auf den Zustand, in dem sich die Fluideigenschaften an einem einzelnen Punkt im System mit der Zeit ändern können. Der stationäre Durchfluss bezieht sich auf den Zustand, in dem sich die Fluideigenschaften ( Temperatur, Druck und Geschwindigkeit ) an einem einzelnen Punkt im System über die Zeit nicht ändern . Eine der wichtigsten Eigenschaften, die in einem stationären Durchflusssystem konstant ist, ist der Systemmassendurchsatz. Dies bedeutet, dass sich in keiner Komponente des Systems Masse ansammelt .
Kontinuitätsgleichung
Die Kontinuitätsgleichung ist einfach ein mathematischer Ausdruck des Prinzips der Massenerhaltung. Für ein Steuervolumen mit einem einzigen Einlass und einem einzigen Auslass besagt das Prinzip der Massenerhaltung, dass für einen stationären Durchfluss der Massenstrom in das Volumen gleich dem Massenstrom aus sein muss.
ṁ in = ṁ out
Masseeintritt pro Zeiteinheit = Massenaustritt pro Zeiteinheit
Diese Gleichung wird als Kontinuitätsgleichung für einen stetigen eindimensionalen Fluss bezeichnet. Für einen stetigen Durchfluss durch ein Kontrollvolumen mit vielen Ein- und Auslässen muss der Nettomassenstrom Null sein, wobei die Zuflüsse negativ und die Abflüsse positiv sind.
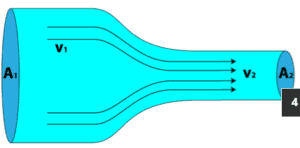
Dieses Prinzip kann auf ein Streamtube wie das oben gezeigte angewendet werden . Es fließt keine Flüssigkeit über die Grenze, die durch die Stromlinien gebildet wird, so dass Masse nur durch die beiden Enden dieses Stromrohrabschnitts eintritt und austritt.
Wenn sich eine Flüssigkeit in Bewegung befindet, muss sie sich so bewegen, dass die Masse erhalten bleibt. Um zu sehen, wie die Massenerhaltung das Geschwindigkeitsfeld einschränkt, berücksichtigen Sie den stetigen Flüssigkeitsfluss durch einen Kanal (dh die Einlass- und Auslassströme variieren nicht mit der Zeit).
Differentialform der Kontinuitätsgleichung
Eine allgemeine Kontinuitätsgleichung kann auch in Differentialform geschrieben werden :
∂⍴ ⁄ ∂t + ∇. (⍴ ͞v) = σ
wo
- ∇. ist Divergenz,
- ρ ist die Dichte der Menge q,
- ⍴ ͞v ist der Fluss der Größe q,
- σ ist die Erzeugung von q pro Volumeneinheit pro Zeiteinheit. Begriffe, die (σ> 0) erzeugen oder (σ <0) q entfernen, werden als “Quellen” bzw. “Senken” bezeichnet. Wenn q eine konservierte Größe ist (z. B. Energie), ist σ gleich 0.
Kontinuitätsgleichung – Mehrere Ein- und Ausgänge
Für ein Kontrollvolumen mit mehreren Ein- und Auslässen erfordert das Prinzip der Massenerhaltung, dass die Summe der Massenströme in das Kontrollvolumen gleich der Summe der Massenströme aus dem Kontrollvolumen ist. Die Kontinuitätsgleichung für diese allgemeinere Situation wird durch die folgende Gleichung ausgedrückt:
∑ṁ in = ∑ṁ out
Summe der pro Zeiteinheit eintretenden Massenströme = Summe der pro Zeiteinheit austretenden Massenströme
Kontinuitätsgleichung – Beispiele
Durchflussrate durch einen Reaktorkern
In diesem Beispiel berechnen wir die Durchflussrate durch einen Reaktorkern aus der Kontinuitätsgleichung. Es ist ein veranschaulichendes Beispiel, die folgenden Daten repräsentieren keine Reaktordesign.
ṁ in = ṁ out
(ρAv) in = (ρAv) out
____________________________
Druckwasserreaktoren werden durch flüssiges Hochdruckwasser ( z . B. 16 MPa )gekühlt und moderiert. Bei diesem Druck kocht Wasser bei ungefähr 350 ° C (662 ° F) . Die Einlasstemperatur des Wassers beträgt ca. 290 ° C ( ~ 720 kg / m 3 ). Das Wasser (Kühlmittel) wird im Reaktorkern auf ungefähr 325 ° C ( ~ 654 kg / m 3 )erhitzt,während das Wasser durch den Kern fließt.
Der Primärkreislauf eines typischen PWR ist in 4 unabhängigeKreisläufe(Rohrdurchmesser ~ 700 mm) unterteilt, wobei jeder Kreislauf einen Dampferzeuger und eine Hauptkühlmittelpumpe umfasst. Im Reaktordruckbehälter (RPV) fließt das Kühlmittel zunächst außerhalb des Reaktorkerns ( durch das Fallrohr ) nach unten . Vom Boden des Druckbehälters wird die Strömung durch den Kern umgekehrt , wo die Kühlmitteltemperatur ansteigt, wenn sie durch die Brennstäbe und die von ihnen gebildeten Baugruppen fließt.
Berechnung:
- der Volumenstrom der Primärleitung (m 3 / s),
- die primäre Rohrströmungsgeschwindigkeit (m / s),
- die Kerneinlassströmungsgeschwindigkeit (m / s),
- die Kernauslassströmungsgeschwindigkeit (m / s)
wann
- Der Massendurchsatz im heißen Abschnitt der Primärleitung beträgt 4648 kg / s .
- Der Reaktorkernströmungsquerschnitt beträgt 5 m 2 ,
- Der primäre Rohrdurchflussquerschnitt (Einzelkreislauf) beträgt 0,38 m 2
Ergebnisse:
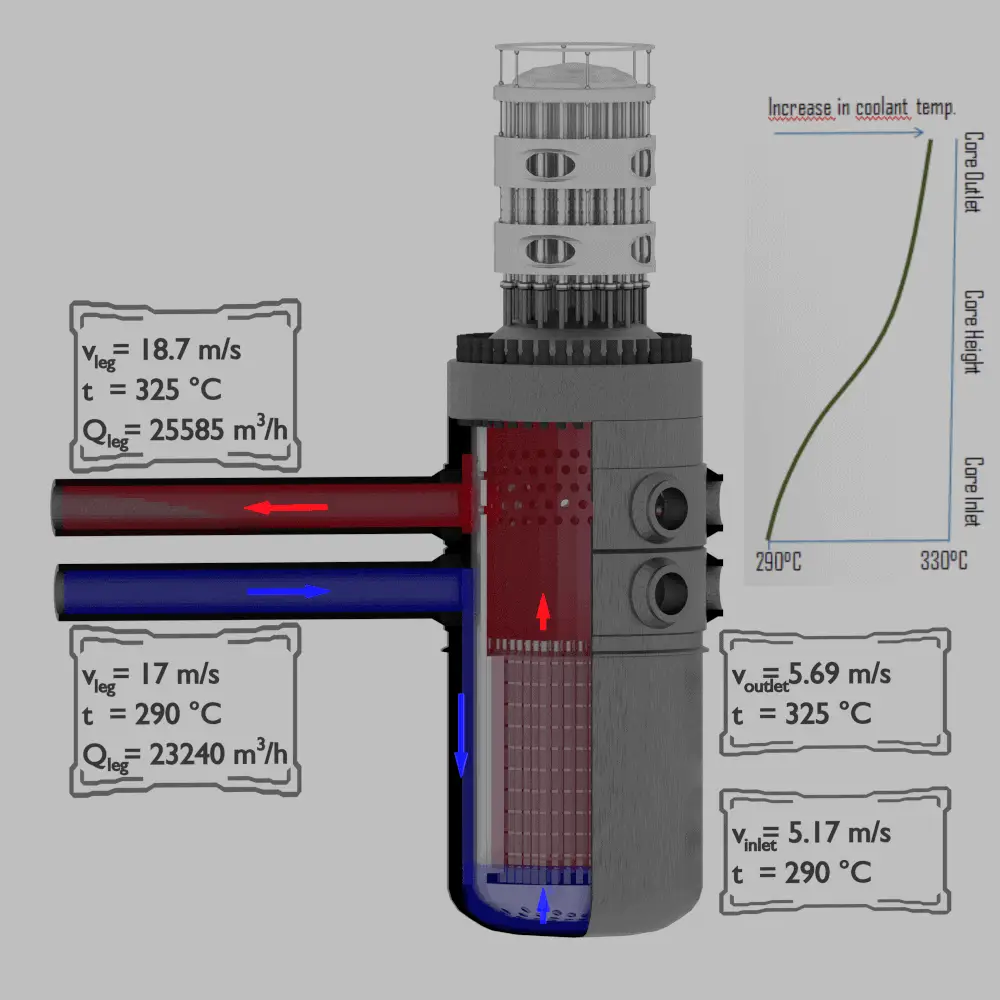
Volumenstrom des kalten Beins:
Q kalt = ṁ / ⍴ = 4648/720 = 6,46 m 3 / s = 23240 m 3 / hod
Fließgeschwindigkeit des kalten Beins:
A 1 = π.d 2 /4
v kalt = Q kalt / A 1 = 6,46 / (3,14 x 0,7 2 /4) = 6,46 / 0,38 = 17 m / s
Volumenstrom des heißen Beins:
Q hot = ṁ / ⍴ = 4648/654 = 7,11 m 3 / s = 25585 m 3 / hod
Fließgeschwindigkeit des heißen Beins:
A = π.d 2 /4
v hot = Q hot / A 1 = 7,11 / (3,14 x 0,7 2 /4) = 7,11 / 0,38 = 18,7 m / s
oder nach der Kontinuitätsgleichung :
⍴ 1 . A 1 . v 1 = ⍴ 2 . A 2 . v 2
v heiß = v kalt . ⍴ kalt / ⍴ heiß = 17 x 720/654 = 18,7 m / s
Kernströmungsgeschwindigkeit:
Ein Kern = 5 m 2
Eine Rohrleitung = 4 x A 1 = 4 x 0,38 = 1,52 m 2
⍴ Einlass = ⍴ kalt
gemäß der Kontinuitätsgleichung :
⍴ Einlass . Ein Kern . v Einlass = ⍴ kalt . Eine Rohrleitung . v kalt
v Einlass = v kalt . A Rohrleitung / A Kern = 17 x 1,52 / 5 = 5,17 m / s
Kernauslassströmungsgeschwindigkeit:
⍴ Einlass = ⍴ kalt
⍴ Steckdose = ⍴ heiß
gemäß der Kontinuitätsgleichung :
⍴ Steckdose . Ein Kern . v Auslass = ⍴ Einlass . Ein Kern . v Einlass
v Auslass = v Einlass . ⍴ Einlass / ⍴ Auslass = 5,17 x 720/654 = 5,69 m / s
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.