Conservación de la masa
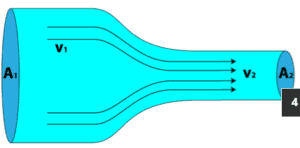
Este principio se conoce generalmente como el principio de conservación de la materia y establece que la masa de un objeto o colección de objetos nunca cambia con el tiempo, sin importar cómo se reorganicen las partes constituyentes. Este principio puede usarse en el análisis de fluidos que fluyen . La conservación de la masa en la dinámica de fluidos establece que todas las tasas de flujo másico en un volumen de control son iguales a todas las tasas de flujo másico fuera del volumen de control más la tasa de cambio de masa dentro del volumen de control. Este principio se expresa matemáticamente mediante la siguiente ecuación:
ṁ in = ṁ out + ∆m ⁄ ∆t
Masa entrando por unidad de tiempo = Masa saliendo por unidad de tiempo + Incremento de masa en el volumen de control por unidad de tiempo

Esta ecuación describe el flujo en estado no estacionario . El flujo en estado no estacionario se refiere a la condición en la que las propiedades del fluido en cualquier punto del sistema pueden cambiar con el tiempo. El flujo en estado estacionario se refiere a la condición en la que las propiedades del fluido ( temperatura, presión y velocidad ) en cualquier punto del sistema no cambian con el tiempo . Pero una de las propiedades más significativas que es constante en un sistema de flujo en estado estacionario es la tasa de flujo másico del sistema. Esto significa que no hay acumulación de masa dentro de ningún componente del sistema.
Ecuación de continuidad
La ecuación de continuidad es simplemente una expresión matemática del principio de conservación de la masa. Para un volumen de control que tiene una sola entrada y una única salida , el principio de conservación de la masa establece que, para el flujo en estado estacionario , la tasa de flujo másico hacia el volumen debe ser igual a la tasa de flujo másico hacia afuera.
ṁ dentro = ṁ fuera
Masa entrando por unidad de tiempo = Masa saliendo por unidad de tiempo
Esta ecuación se llama ecuación de continuidad para flujo unidimensional constante. Para un flujo constante a través de un volumen de control con muchas entradas y salidas, el flujo másico neto debe ser cero, donde las entradas son negativas y las salidas son positivas.
Este principio se puede aplicar a un streamtube como el que se muestra arriba. No fluye fluido a través del límite creado por las líneas de corriente, por lo que la masa solo ingresa y sale a través de los dos extremos de esta sección del tubo de flujo.
Cuando un fluido está en movimiento, debe moverse de tal manera que se conserve la masa. Para ver cómo la conservación de la masa impone restricciones en el campo de velocidad, considere el flujo constante de fluido a través de un conducto (es decir, los flujos de entrada y salida no varían con el tiempo).
Forma diferencial de ecuación de continuidad
Una ecuación de continuidad general también se puede escribir en forma diferencial :
∂⍴ ⁄ ∂t + ∇. (⍴ ͞v) = σ
dónde
- ∇. es divergencia
- ρ es la densidad de la cantidad q,
- ⍴ ͞v es el flujo de la cantidad q,
- σ es la generación de q por unidad de volumen por unidad de tiempo. Los términos que generan (σ> 0) o eliminan (σ <0) q se denominan “fuentes” y “sumideros” respectivamente. Si q es una cantidad conservada (como la energía), σ es igual a 0.
Ecuación de continuidad: múltiples entradas y salidas
Para un volumen de control con múltiples entradas y salidas , el principio de conservación de la masa requiere que la suma de las tasas de flujo másico en el volumen de control sea igual a la suma de las tasas de flujo másico fuera del volumen de control. La ecuación de continuidad para esta situación más general se expresa mediante la siguiente ecuación:
∑ṁ dentro = ∑ṁ fuera
Suma de caudales másicos entrantes por unidad de tiempo = Suma de caudales másicos que salen por unidad de tiempo
Ecuación de continuidad – Ejemplos
Velocidad de flujo a través del núcleo del reactor
En este ejemplo, calcularemos el caudal a través del núcleo del reactor a partir de la ecuación de continuidad. Es un ejemplo ilustrativo, los siguientes datos no representan ningún diseño de reactor.
ṁ dentro = ṁ fuera
(ρAv) in = (ρAv) out
____________________________
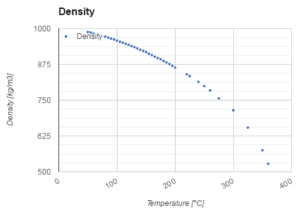
Los reactores de agua a presión se enfrían y moderan con agua líquida a alta presión ( por ejemplo, 16MPa ). A esta presión, el agua hierve a aproximadamente 350 ° C (662 ° F) . La temperatura de entrada del agua es de aproximadamente 290 ° C ( ⍴ ~ 720 kg / m 3 ). El agua (refrigerante) se calienta en el núcleo del reactor a aproximadamente 325 ° C ( ⍴ ~ 654 kg / m 3 ) a medida que el agua fluye a través del núcleo.
El circuito primario de PWR típico se divide en 4 bucles independientes (diámetro de tubería ~ 700 mm), cada bucle comprende un generador de vapor y una bomba de refrigerante principal. Dentro del recipiente a presión del reactor (RPV), el refrigerante primero fluye hacia abajo fuera del núcleo del reactor (a través del tubo de bajada ). Desde el fondo del recipiente a presión, el flujo se invierte a través del núcleo , donde la temperatura del refrigerante aumenta a medida que pasa a través de las barras de combustible y los conjuntos formados por ellas.
Calcular:
- el caudal volumétrico de la tubería primaria (m 3 / s),
- la velocidad de flujo de la tubería primaria (m / s),
- la velocidad del flujo de entrada del núcleo (m / s),
- la velocidad de flujo de salida del núcleo (m / s)
cuando
- La tasa de flujo másico en el tramo caliente de la tubería primaria es igual a 4648 kg / s ,
- La sección transversal del flujo del núcleo del reactor es igual a 5 m 2 ,
- La sección transversal del flujo primario de la tubería (bucle simple) es igual a 0,38 m 2
Resultados:
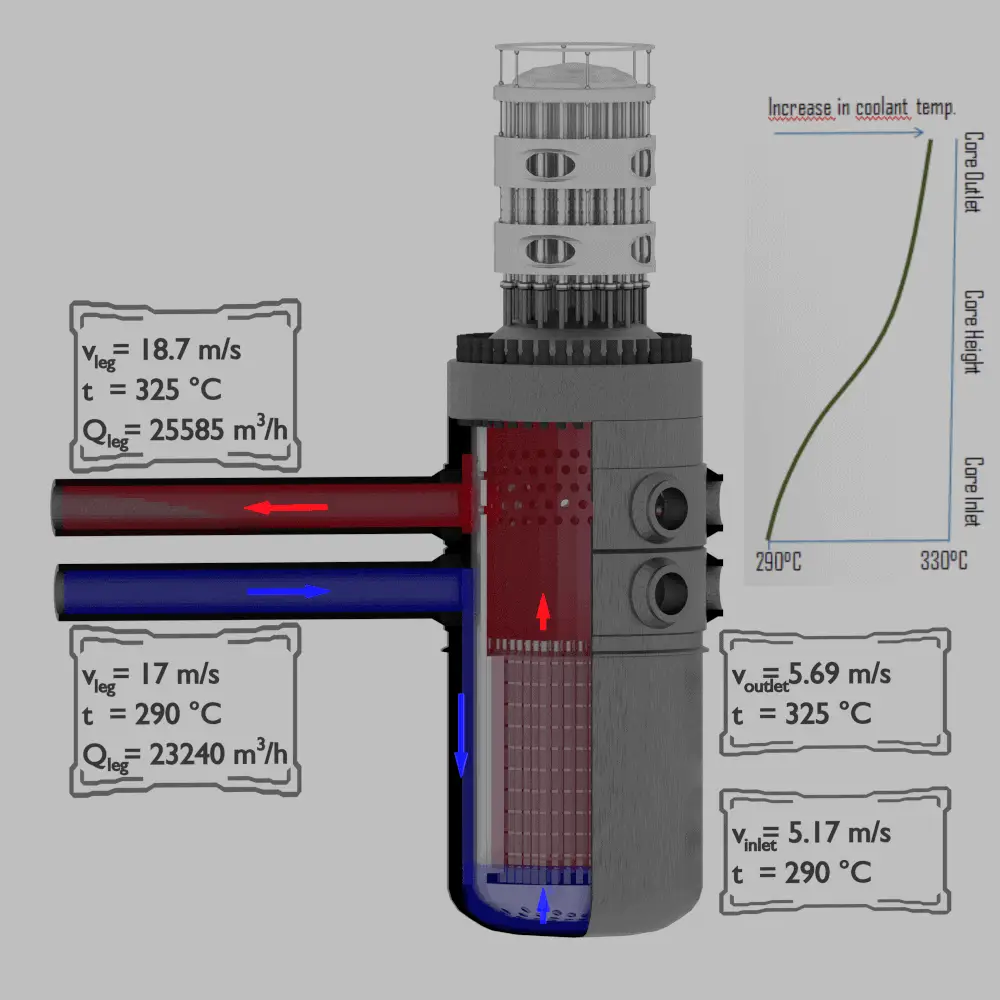
Flujo volumétrico de pierna fría:
Q frío = ṁ / ⍴ = 4648/720 = 6.46 m 3 / s = 23240 m 3 / hod
Velocidad de flujo de pierna fría:
A 1 = π.d 2 /4
v frío = Q frío / A 1 = 6,46 / (3,14 x 0,7 2 /4) = 6,46 / 0,38 = 17 m / s
Caudal volumétrico de pierna caliente:
Q caliente = ṁ / ⍴ = 4648/654 = 7,11 m 3 / s = 25585 m 3 / hod
Velocidad de flujo de la pierna caliente:
A = π.d 2 /4
v caliente = Q caliente / A 1 = 7,11 / (3,14 x 0,7 2 /4) = 7,11 / 0,38 = 18,7 m / s
o de acuerdo con la ecuación de continuidad :
⍴ 1 . A 1 . v 1 = ⍴ 2 . A 2 . v 2
v caliente = v frío . ⍴ frío / ⍴ caliente = 17 x 720/654 = 18.7 m / s
Velocidad de flujo de entrada del núcleo:
Un núcleo = 5 m 2
Una tubería = 4 x A 1 = 4 x 0.38 = 1.52 m 2
⍴ entrada = ⍴ frío
de acuerdo con la ecuación de continuidad :
⍴ entrada . Un núcleo . v entrada = ⍴ frío . Una tubería . v frio
v entrada = v frío . Una tubería / un núcleo = 17 x 1.52 / 5 = 5.17 m / s
Velocidad de flujo de salida del núcleo:
⍴ entrada = ⍴ frío
⍴ salida = ⍴ caliente
de acuerdo con la ecuación de continuidad :
⍴ salida . Un núcleo . v salida = ⍴ entrada . Un núcleo . v entrada
v salida = v entrada . ⍴ entrada / ⍴ salida = 5.17 x 720/654 = 5.69 m / s
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.