Conservação de massa
Esse princípio é geralmente conhecido como o princípio de conservação da massa e afirma que a massa de um objeto ou coleção de objetos nunca muda ao longo do tempo, não importa como as partes constituintes se reorganizem. Este princípio pode ser usado na análise de fluidos fluidos . A conservação de massa na dinâmica de fluidos afirma que todas as taxas de fluxo de massa em um volume de controle são iguais a todas as taxas de fluxo de massa fora do volume de controle mais a taxa de mudança de massa dentro do volume de controle. Este princípio é expresso matematicamente pela seguinte equação:
ṁ in = ṁ fora + ∆m ⁄ ∆t
Entrada de massa por unidade de tempo = Partida de massa por unidade de tempo + Aumento de massa no volume de controle por unidade de tempo

Esta equação descreve o fluxo no estado estacionário . O fluxo em estado estacionário refere-se à condição em que as propriedades do fluido em qualquer ponto único do sistema podem mudar com o tempo. O fluxo no estado estacionário refere-se à condição em que as propriedades do fluido ( temperatura, pressão e velocidade ) em qualquer ponto do sistema não mudam com o tempo . Mas uma das propriedades mais significativas que é constante em um sistema de fluxo em estado estacionário é a taxa de fluxo de massa do sistema. Isso significa que não há acúmulo de massa em nenhum componente do sistema.
Equação de continuidade
A equação de continuidade é simplesmente uma expressão matemática do princípio de conservação de massa. Para um volume de controle que possui uma única entrada e uma única saída , o princípio de conservação de massa afirma que, para o fluxo em estado estacionário , a taxa de fluxo de massa no volume deve ser igual à taxa de fluxo de massa.
ṁ dentro = ṁ fora
Entrada de massa por unidade de tempo = Saída de massa por unidade de tempo
Essa equação é chamada de equação de continuidade para fluxo unidimensional constante. Para um fluxo constante através de um volume de controle com muitas entradas e saídas, o fluxo de massa líquido deve ser zero, onde as entradas são negativas e as saídas são positivas.
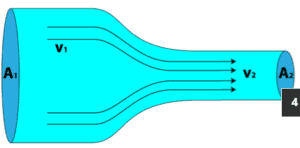
Este princípio pode ser aplicado a um tubo de fluxo como o mostrado acima. Nenhum fluido flui através do limite feito pelas linhas de corrente, de modo que a massa só entra e sai pelas duas extremidades desta seção do tubo de corrente.
Quando um fluido está em movimento, ele deve se mover de maneira que a massa seja conservada. Para ver como a conservação de massa impõe restrições no campo de velocidade, considere o fluxo constante de fluido através de um duto (ou seja, os fluxos de entrada e saída não variam com o tempo).
Forma Diferencial da Equação de Continuidade
Uma equação geral de continuidade também pode ser escrita de forma diferencial :
+ ⁄ ∂t + ∇. (⍴ ͞v) = σ
Onde
- ∇ é divergência,
- ρ é a densidade da quantidade q,
- ͞ ͞v é o fluxo da quantidade q,
- σ é a geração de q por unidade de volume por unidade de tempo. Os termos que geram (σ> 0) ou removem (σ <0) q são referidos como “fontes” e “sumidouros”, respectivamente. Se q é uma quantidade conservada (como energia), σ é igual a 0.
Equação de continuidade – múltiplas entradas e saídas
Para um volume de controle com múltiplas entradas e saídas , o princípio de conservação de massa exige que a soma das taxas de fluxo de massa no volume de controle seja igual à soma das taxas de fluxo de massa fora do volume de controle. A equação de continuidade para essa situação mais geral é expressa pela seguinte equação:
∑ṁ dentro = ∑ṁ fora
Soma das taxas de fluxo de massa entrando por unidade de tempo = Soma das taxas de fluxo de massa saindo por unidade de tempo
Equação de Continuidade – Exemplos
Vazão através de um núcleo de reator
Neste exemplo, calcularemos a taxa de fluxo através de um núcleo de reator a partir da equação de continuidade. É um exemplo ilustrativo, os dados a seguir não representam nenhum projeto de reator.
ṁ dentro = ṁ fora
(ρAv) em = (ρAv) fora
____________________________
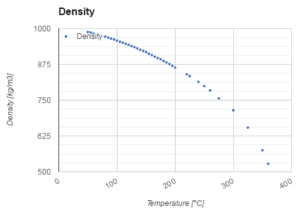
Os reatores de água pressurizada são resfriados e moderados por água líquida de alta pressão ( por exemplo, 16MPa ). A essa pressão, a água ferve a aproximadamente 350 ° C (662 ° F) . A temperatura de entrada da água é de cerca de 290 ° C ( ~ ~ 720 kg / m 3 ). A água (refrigerante) é aquecido no núcleo do reactor para cerca de 325 ° C ( ⍴ ~ 654 kg / m 3 ) medida que a água flui através do núcleo.
O circuito primário da PWR típica é dividido em 4 circuitos independentes (diâmetro da tubulação ~ 700 mm), cada circuito compreende um gerador de vapor e uma bomba de refrigeração principal. Dentro do vaso de pressão do reator (RPV), o líquido de arrefecimento flui primeiro para fora do núcleo do reator ( através do descendente ). Do fundo do vaso de pressão, o fluxo é revertido através do núcleo , onde a temperatura do líquido de refrigeração aumenta à medida que passa pelas barras de combustível e pelos conjuntos formados por elas.
Calcular:
- o caudal volumétrico da tubagem primária (m 3 / s),
- a velocidade do fluxo da tubulação primária (m / s),
- a velocidade do fluxo de entrada do núcleo (m / s),
- a velocidade do fluxo de saída do núcleo (m / s)
quando
- o caudal mássico na perna quente da tubagem primária é igual a 4648 kg / s ,
- A seção transversal do fluxo do núcleo do reator é igual a 5m 2 ,
- A seção transversal do fluxo da tubulação primária (loop único) é igual a 0,38 m 2
Resultados:
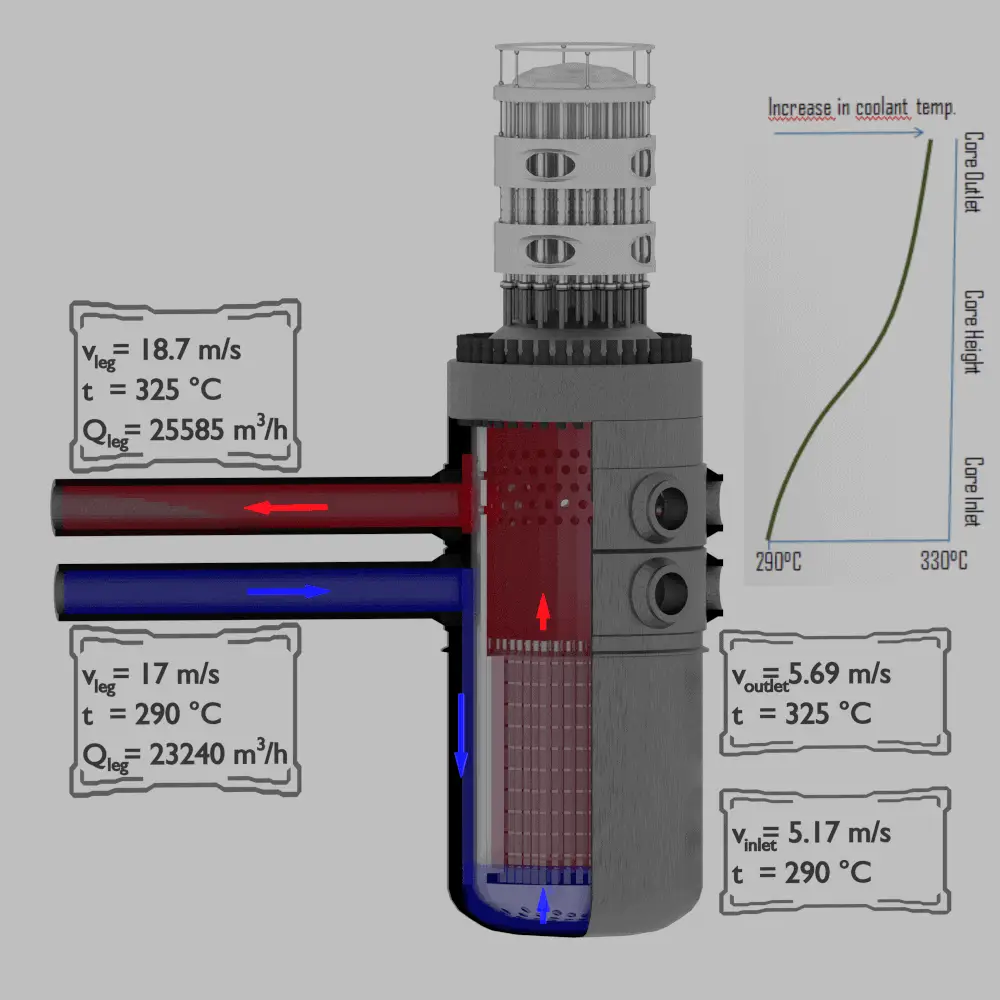
Caudal volumétrico da perna fria:
Q frio = ṁ / ⍴ = 4648/720 = 6,46 m 3 / s = 23240 m 3 / hod
Velocidade de fluxo da perna fria:
Um 1 = π.d 2 /4
v frio = Q frio / A 1 = 6,46 / (3,14 x 0,7 2 /4) = 6,46 / 0,38 = 17 m / s
Caudal volumétrico da perna quente:
Q quente = ṁ / ⍴ = 4648/654 = 7,11 m 3 / s = 25585 m 3 / hod
Velocidade de fluxo da perna quente:
A = π.d 2 /4
v quente = Q quente / A 1 = 7,11 / (3,14 x 0,7 2 /4) = 7,11 / 0,38 = 18,7 m / s
ou de acordo com a equação de continuidade :
⍴ 1 . A 1 . v 1 = ⍴ 2 . A 2 . v 2
v quente = v frio . ⍴ frio / ⍴ quente = 17 x 720/654 = 18,7 m / s
Velocidade do fluxo de entrada do núcleo:
Um núcleo = 5m 2
Uma tubulação = 4 x A 1 = 4 x 0,38 = 1,52 m 2
⍴ entrada = ⍴ frio
de acordo com a equação de continuidade :
Let entrada . Um núcleo . v entrada = ⍴ frio . Uma tubulação . v frio
v entrada = v frio . Uma tubulação / núcleo A = 17 x 1,52 / 5 = 5,17 m / s
Velocidade do fluxo de saída do núcleo:
⍴ entrada = ⍴ frio
⍴ tomada = ⍴ quente
de acordo com a equação de continuidade :
⍴ tomada . Um núcleo . v tomada = entrada . Um núcleo . v entrada
v saída = v entrada . ⍴ entrada / saída = 5,17 x 720/654 = 5,69 m / s
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.