What is Continuity Equation – Definition

Conservation of Mass

This principle is generally known as the conservation of matter principle and states that the mass of an object or collection of objects never changes over time, no matter how the constituent parts rearrange themselves. This principle can be use in the analysis of flowing fluids. Conservation of mass in fluid dynamics states that all mass flow rates into a control volume are equal to all mass flow rates out of the control volume plus the rate of change of mass within the control volume. This principle is expressed mathematically by following equation:

ṁ_in = ṁ_out +^∆m⁄_∆t

Mass entering per unit time = Mass leaving per unit time + Increase of mass in the control volume per unit time

This equation describes nonsteady-state flow. Nonsteady-state flow refers to the condition where the fluid properties at any single point in the system may change over time. Steady-state flow refers to the condition where the fluid properties (temperature, pressure, and velocity) at any single point in the system do not change over time. But one of the most significant properties that is constant in a steady-state flow system is the system mass flow rate. This means that there is no accumulation of mass within any component in the system.

Continuity Equation

The continuity equation is simply a mathematical expression of the principle of conservation of mass. For a control volume that has a single inlet and a single outlet, the principle of conservation of mass states that, for steady-state flow, the mass flow rate into the volume must equal the mass flow rate out.

ṁ_in = ṁ_out 

Mass entering per unit time = Mass leaving per unit time

This equation is called the continuity equation for steady one-dimensional flow. For a steady flow through a control volume with many inlets and outlets, the net mass flow must be zero, where inflows are negative and outflows are positive.

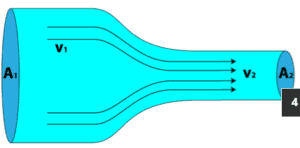
This principle can be applied to a streamtube such as that shown above. No fluid flows across the boundary made by the streamlines so mass only enters and leaves through the two ends of this streamtube section.

When a fluid is in motion, it must move in such a way that mass is conserved. To see how mass conservation places restrictions on the velocity field, consider the steady flow of fluid through a duct (that is, the inlet and outlet flows do not vary with time).

Differential Form of Continuity Equation

A general continuity equation can also be written in a differential form:

^∂⍴⁄_∂t + ∇ . (⍴ ͞v) = σ

where

• ∇ . is divergence,
• ρ is the density of quantity q,
• ⍴ ͞v is the flux of quantity q,
• σ is the generation of q per unit volume per unit time. Terms that generate (σ > 0) or remove (σ < 0) q are referred to as a “sources” and “sinks” respectively. If q is a conserved quantity (such as energy), σ is equal to 0.

Continuity Equation – Multiple Inlets and Outlets

For a control volume with multiple inlets and outlets, the principle of conservation of mass requires that the sum of the mass flow rates into the control volume equal the sum of the mass flow rates out of the control volume. The continuity equation for this more general situation is expressed by following equation:

∑ṁ_in = ∑ṁ_out 

Sum of mass flow rates entering per unit time = Sum of mass flow rates leaving per unit time

Continuity Equation – Examples

Flow rate through a reactor core

In this example, we will calculate the flow rate through a reactor core from continuity equation. It is an illustrative example, following data do not represent any reactor design.

ṁ_in = ṁ_out 

(ρAv)_in = (ρAv)_out 

____________________________

Pressurized water reactors are cooled and moderated by high-pressure liquid water (e.g. 16MPa). At this pressure water boils at approximately 350°C (662°F).  Inlet temperature of the water is about 290°C (⍴ ~ 720 kg/m³). The water (coolant) is heated in the reactor core to approximately 325°C (⍴ ~ 654 kg/m³) as the water flows through the core.
The primary circuit of typical PWR is divided into 4 independent loops (piping diameter ~ 700mm), each loop comprises a steam generator and one main coolant pump. Inside the reactor pressure vessel (RPV), the coolant first flows down outside the reactor core (through the downcomer). From the bottom of the pressure vessel, the flow is reversed up through the core, where the coolant temperature increases as it passes through the fuel rods and the assemblies formed by them.

Calculate:

• the primary piping volumetric flow rate (m³/s),
• the primary piping flow velocity (m/s),
• the core inlet flow velocity (m/s),
• the core outlet flow velocity (m/s)

when

• the mass flow rate in the hot leg of primary piping is equal to 4648 kg/s,
• Reactor core flow cross-section is equal to 5m²,
• Primary piping flow cross-section (single loop) is equal to 0.38 m²

Results:

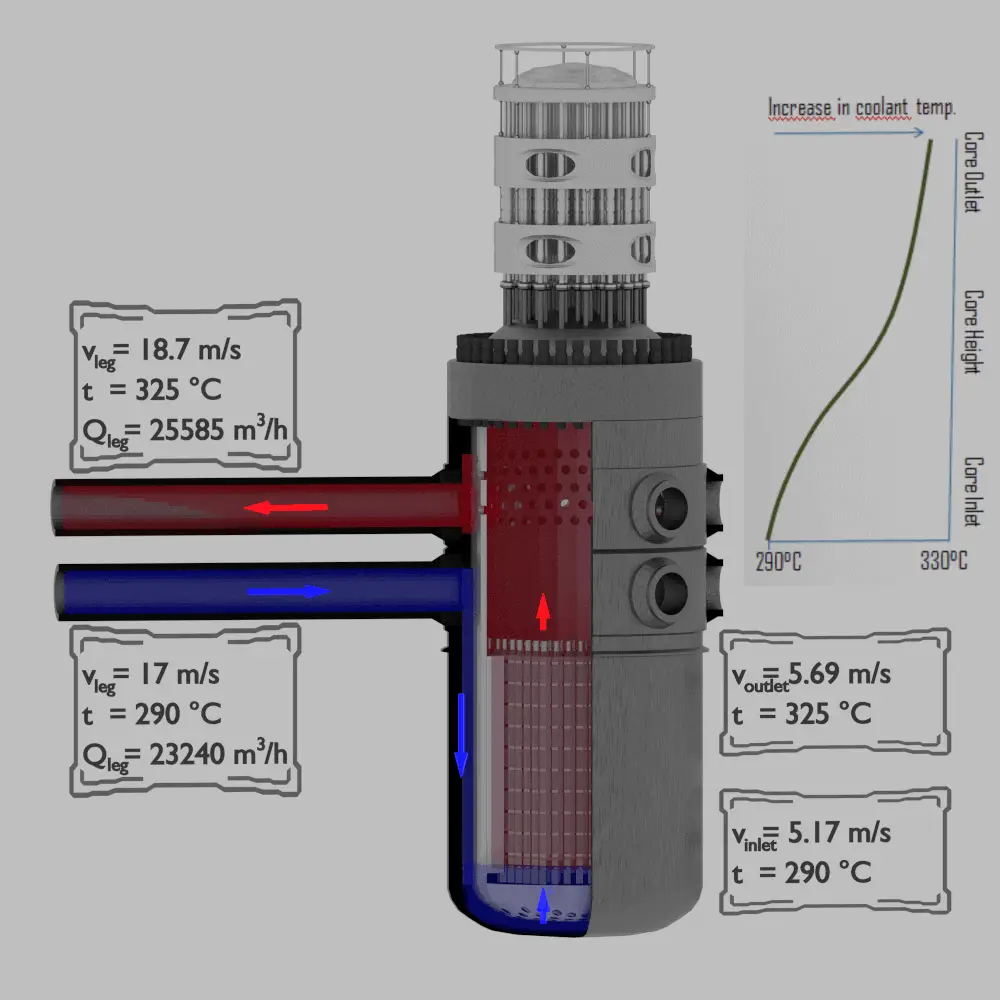
Cold leg volumetric flow rate:

Q_cold = ṁ / ⍴ = 4648 / 720 = 6.46 m³/s = 23240 m³/hod

Cold leg flow velocity:

A₁ = π.d² / 4

v_cold = Q_cold / A₁ = 6.46 / (3.14 x 0.7² / 4) = 6.46 / 0.38 = 17 m/s

Hot leg volumetric flow rate:

Q_hot = ṁ / ⍴ = 4648 / 654 = 7.11 m³/s = 25585 m³/hod

Hot leg flow velocity:

A = π.d² / 4

v_hot = Q_hot / A₁ = 7.11 / (3.14 x 0.7² / 4) = 7.11 / 0.38 = 18,7 m/s

or according to the continuity equation:

⍴₁ . A₁ . v₁ = ⍴₂ . A₂ . v₂

v_hot =  v_cold . ⍴_cold / ⍴_hot = 17 x 720 / 654 = 18.7 m/s

Core inlet flow velocity:

A_core = 5m²

A_piping = 4 x A₁ = 4 x 0.38 = 1.52 m²

⍴_inlet = ⍴_cold

according to the continuity equation:

⍴_inlet . A_core . v_inlet = ⍴_cold . A_piping . v_cold

v_inlet =  v_cold . A_piping / A_core = 17 x 1.52 / 5 = 5.17 m/s

Core outlet flow velocity:

⍴_inlet = ⍴_cold

⍴_outlet = ⍴_hot

according to the continuity equation:

⍴_outlet . A_core . v_outlet = ⍴_inlet . A_core . v_inlet
v_outlet =  v_inlet . ⍴_inlet / ⍴_outlet = 5.17 x 720 / 654 = 5.69 m/s

See also:

Fluid Dynamics