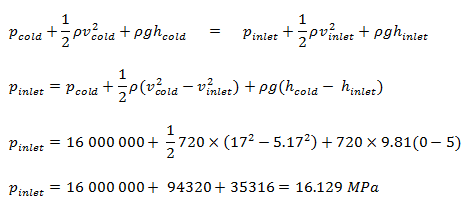Principio de Bernoulli – Ejemplos
Efecto de Bernoulli – Relación entre presión y velocidad
Es un ejemplo ilustrativo, los siguientes datos no corresponden a ningún diseño de reactor.

Cuando la ecuación de Bernoulli se combina con la ecuación de continuidad, las dos se pueden usar para encontrar velocidades y presiones en puntos del flujo conectados por una línea de corriente.
La ecuación de continuidad es simplemente una expresión matemática del principio de conservación de la masa . Para un volumen de control que tiene una sola entrada y una única salida , el principio de conservación de la masa establece que, para el flujo en estado estacionario , la tasa de flujo másico hacia el volumen debe ser igual a la tasa de flujo másico hacia afuera.
Ejemplo:
Determine la presión y la velocidad dentro de un tramo frío de la tubería primaria y determine la presión y la velocidad en el fondo del núcleo del reactor , que está a unos 5 metros por debajo del tramo frío de la tubería primaria.
Dejemos asumir:
- El fluido de densidad constante ⍴ ~ 720 kg / m 3 (a 290 ° C) fluye constantemente a través de la pata fría y a través del fondo del núcleo.
- La sección transversal del flujo primario de la tubería (bucle simple) es igual a 0.385 m 2 (diámetro de la tubería ~ 700 mm)
- La velocidad del flujo en la pierna fría es igual a 17 m / s .
- La sección transversal del flujo del núcleo del reactor es igual a 5 m 2 .
- La presión manométrica dentro de la pierna fría es igual a 16 MPa .
Como resultado del principio de continuidad, la velocidad en la parte inferior del núcleo es:
v entrada = v frío . Una tubería / un núcleo = 17 x 1.52 / 5 = 5.17 m / s
Como resultado del principio de Bernoulli, la presión en la parte inferior del núcleo (entrada del núcleo) es:
Principio de Bernoulli – Fuerza de elevación
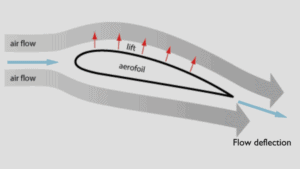
En general, el elevador es una fuerza de acción ascendente en un ala o superficie aerodinámica . Hay varias formas de explicar cómo un perfil aerodinámico genera elevación . Algunas teorías son más complicadas o matemáticamente más rigurosas que otras. Se ha demostrado que algunas teorías son incorrectas. Hay teorías basadas en el principio de Bernoulli y hay teorías basadas directamente en la tercera ley de Newton .
La explicación basada en la tercera ley de Newton establece que el levantamiento es causado por una desviación del flujo de la corriente de aire detrás del perfil aerodinámico. La superficie aerodinámica genera elevación al ejercer una fuerza descendente sobre el aire a medida que pasa. Según la tercera ley de Newton, el aire debe ejercer una fuerza ascendente sobre el perfil . Esta es una explicación muy simple.
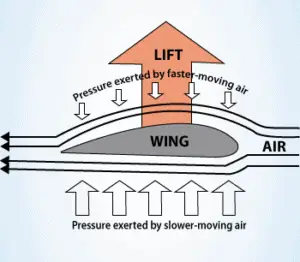
El principio de Bernoulli combinado con la ecuación de continuidad también se puede utilizar para determinar la fuerza de elevación en una superficie de sustentación, si se conoce el comportamiento del flujo de fluido en las proximidades de la lámina. En esta explicación, la forma de un perfil aerodinámico es crucial. La forma de una superficie aerodinámica hace que el aire fluya más rápido en la parte superior que en la inferior. De acuerdo con el principio de Bernoulli , el aire que se mueve más rápido ejerce menos presión y, por lo tanto, el aire debe ejercer una fuerza hacia arriba sobre la superficie de sustentación (como resultado de una diferencia de presión).
El principio de Bernoulli requiere que el perfil aerodinámico tenga una forma asimétrica . Su superficie debe ser mayor en la parte superior que en la inferior. A medida que el aire fluye sobre la superficie de sustentación, es desplazado más por la superficie superior que por la inferior. Según el principio de continuidad , este desplazamiento debe conducir a un aumento en la velocidad del flujo (lo que resulta en una disminución de la presión). La velocidad del flujo aumenta un poco por la superficie inferior del perfil, pero considerablemente menos que el flujo en la superficie superior. La fuerza de elevación de una superficie de sustentación , caracterizada por el coeficiente de elevación , se puede cambiar durante el vuelo mediante cambios en la forma de una superficie de sustentación . Por lo tanto, el coeficiente de elevación puede incluso duplicarse con dispositivos relativamente simples (aletas y listones ) si se usan en todo el tramo del ala.El uso del principio de Bernoulli puede no ser correcto. El principio de Bernoulli supone la incompresibilidad del aire, pero en realidad el aire es fácilmente compresible. Pero hay más limitaciones de explicaciones basadas en el principio de Bernoulli. Hay dos explicaciones populares principales de ascensor:
- Explicación basada en la desviación hacia abajo del flujo: la tercera ley de Newton
- Explicación basada en cambios en la velocidad y presión del flujo: principio de continuidad y principio de Bernoulli
Ambas explicaciones identifican correctamente algunos aspectos de las fuerzas de elevación, pero dejan otros aspectos importantes del fenómeno sin explicar. Una explicación más completa implica tanto cambios en la velocidad del flujo como en la desviación hacia abajo y requiere observar el flujo con más detalle.
Ver más: Doug McLean, Understanding Aerodynamics: Arguing from the Real Physics. John Wiley & Sons Ltd. 2013. ISBN: 978-1119967514
Efecto de Bernoulli: bola giratoria en un flujo de aire
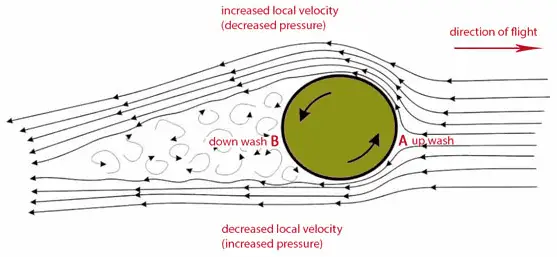 El efecto de Bernoulli tiene otra consecuencia interesante e interesante. Supongamos que un balón está girando a medida que viaja por el aire. A medida que la bola gira, la fricción superficial de la bola con el aire circundante arrastra una capa delgada (denominada capa límite ) de aire con ella. Se puede ver en la imagen que la capa límite está en un lado viajando en la misma dirección que la corriente de aire que fluye alrededor de la pelota (la flecha superior) y en el otro lado, la capa límite está viajando en la dirección opuesta ( la flecha inferior). En el lado de la pelota donde la corriente de aire y la capa límite se mueven en la dirección opuesta (la flecha inferior) entre sí, la fricción entre los dosralentiza la corriente de aire . En el lado opuesto, estas capas se mueven en la misma dirección y la corriente se mueve más rápido .
El efecto de Bernoulli tiene otra consecuencia interesante e interesante. Supongamos que un balón está girando a medida que viaja por el aire. A medida que la bola gira, la fricción superficial de la bola con el aire circundante arrastra una capa delgada (denominada capa límite ) de aire con ella. Se puede ver en la imagen que la capa límite está en un lado viajando en la misma dirección que la corriente de aire que fluye alrededor de la pelota (la flecha superior) y en el otro lado, la capa límite está viajando en la dirección opuesta ( la flecha inferior). En el lado de la pelota donde la corriente de aire y la capa límite se mueven en la dirección opuesta (la flecha inferior) entre sí, la fricción entre los dosralentiza la corriente de aire . En el lado opuesto, estas capas se mueven en la misma dirección y la corriente se mueve más rápido .
Según el principio de Bernoulli , el aire que se mueve más rápido ejerce menos presión y, por lo tanto, el aire debe ejercer una fuerza hacia arriba sobre la pelota. De hecho, en este caso el uso del principio de Bernoulli puede no ser correcto. El principio de Bernoulli supone la incompresibilidad del aire, pero en realidad el aire es fácilmente compresible. Pero hay más limitaciones de explicaciones basadas en el principio de Bernoulli.
El trabajo de Robert G. Watts y Ricardo Ferrer (Las fuerzas laterales en una esfera giratoria: Aerodinámica de una bola curva) este efecto puede explicarse por otro modelo que presta atención importante a la capa límite de aire giratorio alrededor de la pelota. En el lado de la pelota donde la corriente de aire y la capa límite se mueven en la dirección opuesta (la flecha inferior), la capa límite tiende a separarse prematuramente. En el lado de la bola donde la corriente de aire y la capa límite se mueven en la misma dirección, la capa límite se transporta más alrededor de la bola antes de separarse en un flujo turbulento. Esto da una desviación de flujode la corriente de aire en una dirección detrás de la pelota. La bola giratoria genera elevación al ejercer una fuerza descendente sobre el aire a medida que pasa. Según la tercera ley de Newton , el aire debe ejercer una fuerza hacia arriba sobre la pelota.
Ley de Torricelli

La ley de Torricelli , también conocida como el principio de Torricelli , o el teorema de Torricelli , afirma en dinámica de fluidos que la velocidad, v, del fluido que fluye de un orificio bajo la fuerza de gravedad en un tanque es proporcional a la raíz cuadrada de la distancia vertical, h , entre la superficie del líquido y el centro del orificio y hasta la raíz cuadrada del doble de la aceleración causada por la gravedad (g = 9.81 N / kg cerca de la superficie de la tierra).
En otras palabras, la velocidad de salida del fluido del orificio es la misma que habría adquirido al caer una altura h bajo la gravedad. La ley fue descubierta y nombrada en honor al científico italiano Evangelista Torricelli , en 1643. Más tarde se demostró que era un caso particular del principio de Bernoulli .
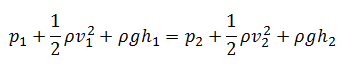
La ecuación de Torricelli se deriva para una condición específica. El orificio debe ser pequeño y la viscosidad y otras pérdidas deben ser ignoradas. Si un fluido fluye a través de un orificio muy pequeño (por ejemplo, en el fondo de un tanque grande), entonces la velocidad del fluido en el extremo grande puede despreciarse en la ecuación de Bernoulli. Además, la velocidad del flujo de salida es independiente de la dirección del flujo. En ese caso, la velocidad de salida del fluido que fluye a través del orificio viene dada por la siguiente fórmula:
v = √ 2gh
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.