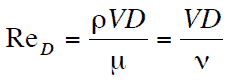Números característicos
En dinámica de fluidos y transferencia de calor , los números característicos son números adimensionales utilizados para describir un carácter del flujo o para describir un carácter de transferencia de calor. Los números característicos se pueden usar para comparar una situación real (p. Ej., Flujo de aire alrededor de una superficie de sustentación y flujo de agua en una tubería) con un modelo a pequeña escala . Es necesario mantener iguales los números característicos importantes. Los nombres de estos números se estandarizaron en ISO 31-12 , que proporciona el nombre, el símbolo y la definición de 25 números característicos seleccionados utilizados para la descripción de los fenómenos de transporte.
Numero Reynolds
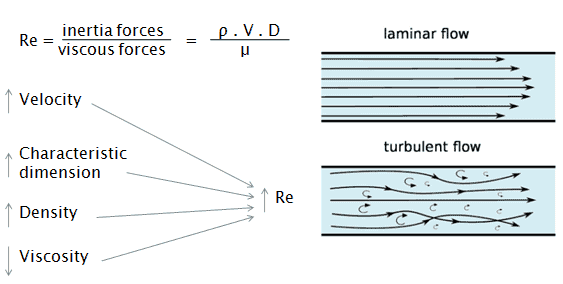
El número de Reynolds es la relación de fuerzas de inercia a fuerzas viscosas y es un parámetro conveniente para predecir si una condición de flujo será laminar o turbulento . Se puede interpretar que cuando las fuerzas viscosas son dominantes (flujo lento, bajo Re ) son suficientes para mantener todas las partículas de fluido en línea, entonces el flujo es laminar. Incluso Re muy bajo indica un movimiento de arrastre viscoso, donde los efectos de inercia son insignificantes. Cuando las fuerzas de inercia dominan sobre las fuerzas viscosas (cuando el fluido fluye más rápido y Re es más grande), el flujo es turbulento.
Es un número adimensional compuesto por las características físicas del flujo. Un número creciente de Reynolds indica una turbulencia creciente del flujo.
donde:
V es la velocidad del flujo,
D es una dimensión lineal característica (longitud recorrida del fluido; diámetro hidráulico, etc.)
ρ densidad del fluido (kg / m 3 ),
μ viscosidad dinámica (Pa.s),
ν viscosidad cinemática ( m 2 / s); ν = μ / ρ.
Número Prandtl
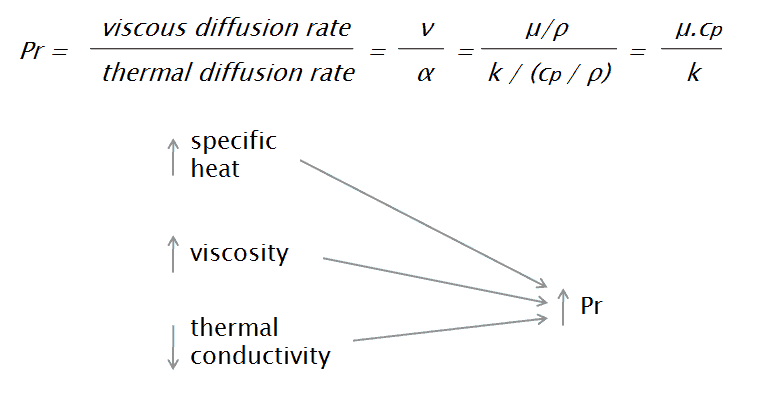
El número de Prandtl es un número adimensional, llamado así por su inventor, el ingeniero alemán Ludwig Prandtl , quien también identificó la capa límite . El número de Prandtl se define como la relación de difusividad impulso a la difusividad térmica . La difusividad de momento , o como se le llama normalmente, viscosidad cinemática, nos dice la resistencia del material a los flujos de corte (diferentes capas del flujo viajan con diferentes velocidades debido, por ejemplo, a diferentes velocidades de paredes adyacentes) en relación con la densidad. Es decir, el número de Prandtl se da como:
dónde:
ν es la difusividad de momento (viscosidad cinemática) [m 2 / s]
α es difusividad térmica [m 2 / s]
μ es la viscosidad dinámica [Ns / m 2 ]
k es conductividad térmica [W / mK]
c p es calor específico [J / kg.K]
ρ es densidad [kg / m 3 ]
Pequeños valores del número de Prandtl , Pr <<1 , significa que domina la difusividad térmica. Mientras que con valores grandes, Pr >> 1 , la difusividad de momento domina el comportamiento. Por ejemplo, el valor típico para el mercurio líquido, que es aproximadamente 0.025, indica que la conducción de calor es más significativa en comparación con la convección , por lo que la difusividad térmica es dominante. Cuando Pr es pequeño, significa que el calor se difunde rápidamente en comparación con la velocidad.
En comparación con el número de Reynolds , el número de Prandtl no depende de la geometría de un objeto involucrado en el problema, sino que depende únicamente del fluido y del estado del fluido. Como tal, el número de Prandtl a menudo se encuentra en las tablas de propiedades junto con otras propiedades como la viscosidad y la conductividad térmica.
Ver también: número de Prandtl
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.