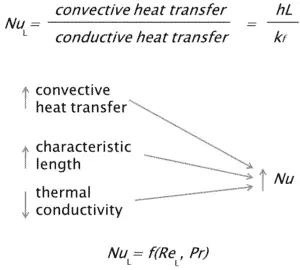
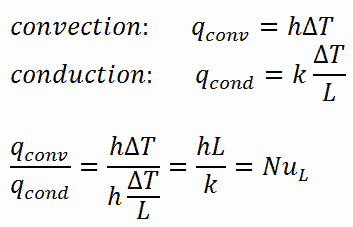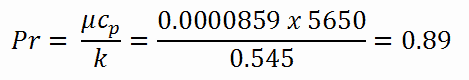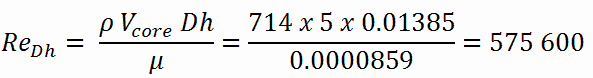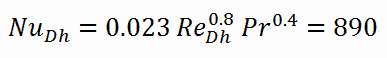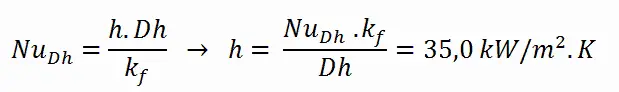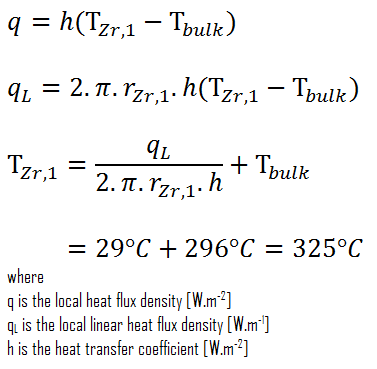Nusselt Number
El número de Nusselt es un número adimensional, llamado así por un ingeniero alemán Wilhelm Nusselt. El número de Nusselt está estrechamente relacionado con el número de Péclet y ambos números se usan para describir la relación de la energía térmica que se convence al fluido con respecto a la energía térmica conducida dentro del fluido. El número de Nusselt es igual al gradiente de temperatura adimensional en la superficie, y proporciona una medida de la transferencia de calor por convección que ocurre en la superficie. El componente conductor se mide en las mismas condiciones que la convección de calor pero con un fluido estancado. El número de Nusseltes para la capa límite térmica lo que es el coeficiente de fricción para la capa límite de velocidad. Por lo tanto, el número de Nusselt se define como:
dónde:
k f es la conductividad térmica del fluido [W / mK]
L es la longitud característica
h es el coeficiente de transferencia de calor por convección [W / m 2 .K]
Para ilustración, considere una capa de fluido de espesor L y diferencia de temperatura ΔT . La transferencia de calor a través de la capa de fluido se realizará por convección cuando el fluido implique algún movimiento y por conducción cuando la capa de fluido esté inmóvil.
En caso de conducción , el flujo de calor puede calcularse utilizando la ley de conducción de Fourier . En caso de convección, el flujo de calor se puede calcular utilizando la ley de enfriamiento de Newton. Tomando su proporción da:
La ecuación anterior define el número de Nusselt . Por lo tanto, el número de Nusselt representa la mejora de la transferencia de calor a través de una capa de fluido como resultado de la convección en relación con la conducción a través de la misma capa de fluido. Un número de Nusselt de Nu = 1 para una capa de fluido representa la transferencia de calor a través de la capa por conducción pura . Cuanto mayor sea el número de Nusselt , más efectiva será la convección. Un número mayor de Nusselt corresponde a una convección más efectiva, con un flujo turbulento típicamente en el rango de 100-1000. Para flujo turbulento, el número de Nusselt suele ser una función del número de Reynolds y elNúmero Prandtl .
Número de Nusselt para reactores de metal líquido
Ver también: número de Nusselt para reactores de metal líquido
Para metales líquidos, el número de Prandtl es muy pequeño, generalmente en el rango de 0.01 a 0.001. Esto significa que la difusividad térmica , que está relacionada con la velocidad de transferencia de calor por conducción , domina inequívocamente . Esta muy alta difusividad térmica resulta de una conductividad térmica muy alta de los metales, que es aproximadamente 100 veces mayor que la del agua. El número de Prandtl para sodio a una temperatura de funcionamiento típica en los reactores rápidos enfriados con sodio es de aproximadamente 0,004. Para este caso, el desarrollo de la capa límite térmica es mucho más rápido que el de la capa límite de velocidad (δ t >> δ), y es razonable suponer una velocidad uniforme en toda la capa límite térmica.
Los coeficientes de transferencia de calor para el flujo de sodio a través del canal de combustible se basan en el número de Prandtl y el número de Péclet . Paso a diámetro (P / D) también ingresa muchos cálculos de transferencia de calor en reactores de metal líquido. Las correlaciones de transferencia de calor por convección generalmente se presentan en términos de número de Nusselt versus número de Péclet . El número típico de Péclet para el funcionamiento normal es de 150 a 300 en los paquetes de combustible. En cuanto a otros regímenes de flujo, el número de Nusselt y una correlación dada pueden usarse para determinar el coeficiente de transferencia de calor por convección.
Ejemplo: número de Nusselt: temperatura de la superficie del revestimiento
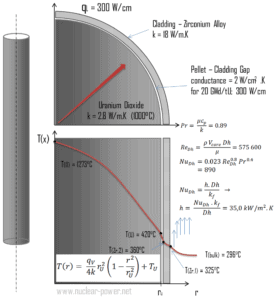El revestimiento es la capa externa de las barras de combustible, que se encuentra entre el refrigerante del reactor y el combustible nuclear (es decir, las pastillas de combustible ). Está hecho de un material resistente a la corrosión con una sección transversal de baja absorción para neutrones térmicos , generalmente aleación de circonio . El revestimiento evita que los productos de fisión radiactiva escapen de la matriz de combustible hacia el refrigerante del reactor y lo contaminen. El revestimiento constituye una de las barreras en el enfoque de ‘ defensa en profundidad ‘, por lo tanto, su capacidad de enfriamiento es uno de los aspectos clave de seguridad.
Considere el revestimiento de combustible del radio interno r Zr, 2 = 0.408 cm y el radio externo r Zr, 1 = 0.465 cm . En comparación con el granulado de combustible, casi no hay generación de calor en el revestimiento de combustible (el revestimiento se calienta ligeramente por radiación ). Todo el calor generado en el combustible debe transferirse por conducción a través del revestimiento y, por lo tanto, la superficie interna está más caliente que la superficie externa.
Asumir que:
- El diámetro exterior del revestimiento es: d = 2 xr Zr, 1 = 9,3 mm
- El paso de los pasadores de combustible es: p = 13 mm
- La conductividad térmica del agua saturada a 300 ° C es: k H2O = 0.545 W / mK
- La viscosidad dinámica del agua saturada a 300 ° C es: μ = 0.0000859 Ns / m 2
- la densidad del fluido es: ρ = 714 kg / m 3
- el calor específico es: c p = 5,65 kJ / kg.K
- la velocidad del flujo central es constante e igual a V core = 5 m / s
- La temperatura del refrigerante del reactor en esta coordenada axial es: T a granel = 296 ° C
- la tasa de calor lineal del combustible es q L = 300 W / cm (F Q ≈ 2.0) y, por lo tanto, la tasa de calor volumétrica es q V = 597 x 10 6 W / m 3
Calcule el número de Prandtl , Reynolds y Nusselt para este régimen de flujo (flujo turbulento forzado interno) dentro de la red de combustible rectangular (canal de combustible), luego calcule el coeficiente de transferencia de calor y finalmente la temperatura de la superficie del revestimiento , T Zr, 1 .
Para calcular la temperatura de la superficie del revestimiento , tenemos que calcular el número de Prandtl , Reynolds y Nusselt , porque la transferencia de calor para este régimen de flujo puede describirse mediante la ecuación de Dittus-Boelter , que es:
Cálculo del número de Prandtl
Para calcular el número de Prandtl , tenemos que saber:
- La conductividad térmica del agua saturada a 300 ° C es: k H2O = 0.545 W / mK
- La viscosidad dinámica del agua saturada a 300 ° C es: μ = 0.0000859 Ns / m 2
- el calor específico es: c p = 5,65 kJ / kg.K
Tenga en cuenta que todos estos parámetros difieren significativamente para el agua a 300 ° C de aquellos a 20 ° C. El número de Prandtl para agua a 20 ° C es de alrededor de 6.91. El número de Prandtl para el refrigerante del reactor a 300 ° C es entonces:
Cálculo del número de Reynolds.
Para calcular el número de Reynolds, tenemos que saber:
- El diámetro exterior del revestimiento es: d = 2 xr Zr, 1 = 9,3 mm (para calcular el diámetro hidráulico)
- El paso de los pasadores de combustible es: p = 13 mm (para calcular el diámetro hidráulico)
- La viscosidad dinámica del agua saturada a 300 ° C es: μ = 0.0000859 Ns / m 2
- la densidad del fluido es: ρ = 714 kg / m 3
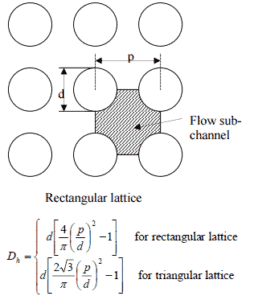
El diámetro hidráulico, D h , es un término comúnmente utilizado cuando se maneja el flujo en tubos y canales no circulares . El diámetro hidráulico del canal de combustible , D h , es igual a 13,85 mm.
Ver también: diámetro hidráulico
El número de Reynolds dentro del canal de combustible es igual a:
Esto satisface completamente las condiciones turbulentas .
Cálculo del número de Nusselt usando la ecuación de Dittus-Boelter
Para un flujo turbulento completamente desarrollado (hidrodinámicamente y térmicamente) en un tubo circular liso, el número local de Nusselt se puede obtener de la conocida ecuación Dittus ?? Boelter .
Para calcular el número de Nusselt , tenemos que saber:
- el número de Reynolds , que es Re Dh = 575600
- el número de Prandtl , que es Pr = 0.89
El número de Nusselt para la convección forzada dentro del canal de combustible es igual a:
Cálculo del coeficiente de transferencia de calor y la temperatura de la superficie del revestimiento, T Zr, 1
El conocimiento detallado de la geometría, los parámetros del fluido, el radio exterior del revestimiento, la tasa de calor lineal, el coeficiente de transferencia de calor por convección nos permite calcular la diferencia de temperatura ∆T entre el refrigerante (T volumen ) y la superficie del revestimiento (T Zr, 1 ).
Para calcular la temperatura de la superficie del revestimiento, debemos saber:
- El diámetro exterior del revestimiento es: d = 2 x r Zr, 1 = 9,3 mm
- el número de Nusselt, que es Nu Dh = 890
- El diámetro hidráulico del canal de combustible es: D h = 13,85 mm
- La conductividad térmica del refrigerante del reactor (300 ° C) es: k H2O = 0.545 W / mK
- La temperatura total del refrigerante del reactor en esta coordenada axial es: T mayor = 296 ° C
- La tasa de calor lineal del combustible es: q L = 300 W / cm (F Q ≈ 2.0)
El coeficiente de transferencia de calor por convección, h , viene dado directamente por la definición del número de Nusselt:
Finalmente, podemos calcular la temperatura de la superficie del revestimiento (T Zr, 1 ) simplemente usando la Ley de Enfriamiento de Newton :
Para los PWR en funcionamiento normal, hay un agua líquida comprimida dentro del núcleo del reactor, bucles y generadores de vapor. La presión se mantiene a aproximadamente 16MPa . A esta presión, el agua hierve a aproximadamente 350 ° C (662 ° F). Como se puede ver, la temperatura de la superficie T Zr, 1 = 325 ° C garantiza que ni siquiera se produce una ebullición subenfriada. Tenga en cuenta que, la ebullición subenfriada requiere T Zr, 1 = T sat . Dado que las temperaturas de entrada del agua suelen ser de unos 290 ° C(554 ° F), es obvio que este ejemplo corresponde a la parte inferior del núcleo. A elevaciones más altas del núcleo, la temperatura aparente puede alcanzar hasta 330 ° C. La diferencia de temperatura de 29 ° C hace que se produzca la ebullición subenfriada (330 ° C + 29 ° C> 350 ° C). Por otro lado, la ebullición de nucleados en la superficie altera efectivamente la capa estancada y, por lo tanto, la ebullición de nucleados aumenta significativamente la capacidad de una superficie para transferir energía térmica al fluido a granel. Como resultado, el coeficiente de transferencia de calor por convección aumenta significativamente y, por lo tanto, a elevaciones más altas, la diferencia de temperatura (T Zr, 1 – T a granel ) disminuye significativamente.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
