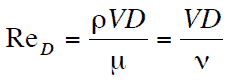Kennzahlen
In der Fluiddynamik und der Wärmeübertragung sind Kennzahlen dimensionslose Zahlen, mit denen ein Charakter der Strömung oder ein Charakter der Wärmeübertragung beschrieben wird. Kennzahlen können verwendet werden, um eine reale Situation (z. B. Luftströmung um ein Schaufelblatt und Wasserströmung in einem Rohr) mit einem Modell im kleinen Maßstab zu vergleichen . Es ist notwendig, die wichtigen Kennzahlen gleich zu halten. Die Bezeichnungen dieser Nummern wurden in ISO 31-12 standardisiert , die Namen, Symbole und Definitionen für 25 ausgewählte Kennnummern enthält, die zur Beschreibung von Transportphänomenen verwendet werden.
Reynolds Nummer
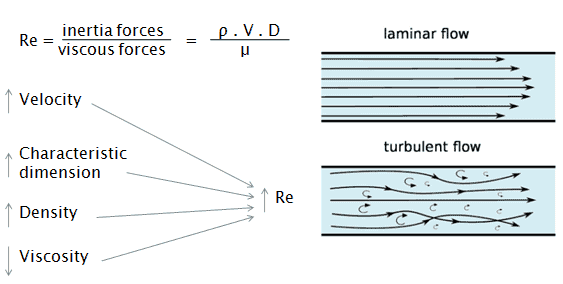
Die Reynoldszahl ist das Verhältnis von Trägheitskräften zu viskosen Kräften und ein geeigneter Parameter zur Vorhersage, ob ein Strömungszustand laminar oder turbulent sein wird . Es kann interpretiert werden, dass, wenn die viskosen Kräfte dominant sind (langsamer Fluss, niedriger Re ), sie ausreichen, um alle Fluidpartikel in einer Linie zu halten, der Fluss laminar ist. Sogar ein sehr niedriger Re- Wert zeigt eine viskose Kriechbewegung an, bei der Trägheitseffekte vernachlässigbar sind. Wenn die Trägheitskräfte die Viskositätskräfte überwiegen (wenn das Fluid schneller fließt und Re größer ist), ist die Strömung turbulent.
Es ist eine dimensionslose Zahl, die sich aus den physikalischen Eigenschaften der Strömung zusammensetzt. Eine zunehmende Reynoldszahl zeigt eine zunehmende Strömungsturbulenz an.
wobei:
V die Strömungsgeschwindigkeit ist,
D eine charakteristische lineare Abmessung ist (zurückgelegte Länge des Fluids; hydraulischer Durchmesser usw.)
ρ Fluiddichte (kg / m 3 ),
μ dynamische Viskosität (Pa.s),
ν kinematische Viskosität ( m 2 / s); ν = μ / ρ.
Prandtl-Nummer
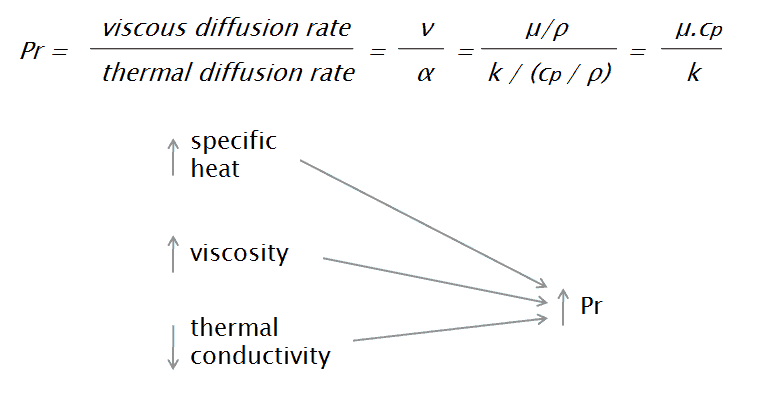
Die Prandtl-Zahl ist eine dimensionslose Zahl, benannt nach ihrem Erfinder, einem deutschen Ingenieur Ludwig Prandtl , der auch die Grenzschicht identifizierte . Die Prandtl-Zahl ist definiert als das Verhältnis von Impulsdiffusionsvermögen zu thermischem Diffusionsvermögen . Die Impulsdiffusionsfähigkeit oder, wie es normalerweise genannt wird, kinematische Viskosität gibt Auskunft über den Widerstand des Materials gegen Scherströmungen (verschiedene Schichten der Strömung bewegen sich mit unterschiedlichen Geschwindigkeiten, z. B. aufgrund unterschiedlicher Geschwindigkeiten benachbarter Wände) in Bezug auf die Dichte. Das heißt, die Prandtl-Nummer lautet:
wo:
ν ist die Impulsdiffusionsfähigkeit (kinematische Viskosität) [m 2 / s]
α ist die Wärmeleitfähigkeit [m 2 / s]
μ ist die dynamische Viskosität [Ns / m 2 ]
k ist die Wärmeleitfähigkeit [W / mK]
c p ist die spezifische Wärme [J / kg.K]
ρ ist die Dichte [kg / m 3 ]
Kleine Werte der Prandtl-Zahl , Pr << 1 , bedeuten, dass das thermische Diffusionsvermögen dominiert. Während bei großen Werten Pr >> 1 die Impulsdiffusionsfähigkeit das Verhalten dominiert. Beispielsweise zeigt der typische Wert für flüssiges Quecksilber, der etwa 0,025 beträgt, dass die Wärmeleitung im Vergleich zur Konvektion signifikanter ist , so dass die Wärmeleitfähigkeit dominiert. Wenn Pr klein ist, bedeutet dies, dass die Wärme im Vergleich zur Geschwindigkeit schnell diffundiert.
Im Vergleich zur Reynolds-Zahl hängt die Prandtl-Zahl nicht von der Geometrie eines am Problem beteiligten Objekts ab, sondern ausschließlich von der Flüssigkeit und dem Flüssigkeitszustand. Daher wird die Prandtl-Zahl häufig in Eigenschaftentabellen neben anderen Eigenschaften wie Viskosität und Wärmeleitfähigkeit gefunden.
Siehe auch: Prandtl-Nummer
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.