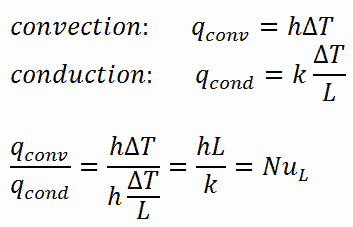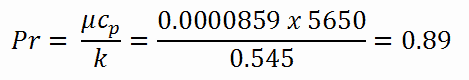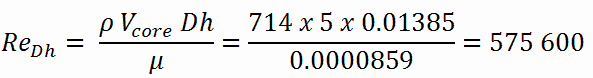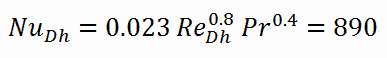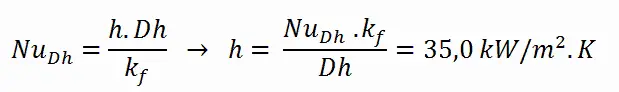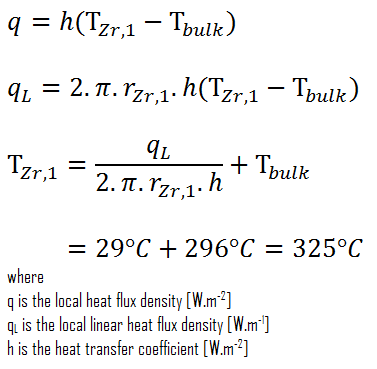Qu’est-ce que le nombre Nusselt – Définition

Nombre de Nusselt

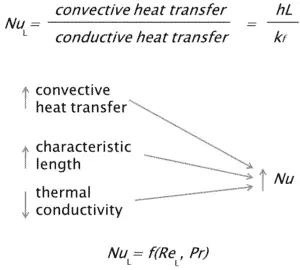
Le nombre Nusselt est un nombre sans dimension, nommé d’après un ingénieur allemand Wilhelm Nusselt. Le nombre de Nusselt est étroitement lié au nombre de Péclet et les deux nombres sont utilisés pour décrire le rapport de l’ énergie thermique convectée au fluide à l’ énergie thermique conduite dans le fluide. Le nombre de Nusselt est égal au gradient de température sans dimension à la surface, et il fournit une mesure du transfert de chaleur par convection se produisant à la surface. La composante conductrice est mesurée dans les mêmes conditions que la convection thermique mais avec un fluide stagnant. Le numéro de Nusseltest à la couche limite thermique ce que le coefficient de frottement est à la couche limite de vitesse. Ainsi, le nombre de Nusselt est défini comme:

où:

k _f est la conductivité thermique du fluide [W / mK]

L est la longueur caractéristique

h est le coefficient de transfert de chaleur par convection [W / m ² .K]

À titre d’illustration, considérons une couche fluide d’épaisseur L et de différence de température ΔT . Le transfert de chaleur à travers la couche de fluide se fera par convection lorsque le fluide implique un certain mouvement et par conduction lorsque la couche de fluide est immobile.

En cas de conduction , le flux de chaleur peut être calculé en utilisant la loi de conduction de Fourier . En cas de convection, le flux de chaleur peut être calculé en utilisant la loi de Newton du refroidissement. Prendre leur rapport donne:

L’équation précédente définit le nombre de Nusselt . Par conséquent, le nombre de Nusselt représente l’amélioration du transfert de chaleur à travers une couche de fluide en raison de la convection relative à la conduction à travers la même couche de fluide. Un nombre Nusselt de Nu = 1 pour une couche fluide représente le transfert de chaleur à travers la couche par conduction pure . Plus le nombre de Nusselt est élevé , plus la convection est efficace. Un nombre de Nusselt plus grand correspond à une convection plus efficace, avec un écoulement turbulent typiquement dans la gamme 100–1000. Pour un écoulement turbulent, le nombre de Nusselt est généralement fonction du nombre de Reynolds et duNuméro Prandtl .

Corrélations – Débit de fluide monophasé

Nombre de Nusselt pour les réacteurs à métal liquide

Voir aussi: Nombre de Nusselt pour les réacteurs à métal liquide

Pour les métaux liquides, le nombre de Prandtl est très faible, généralement compris entre 0,01 et 0,001. Cela signifie que la diffusivité thermique , qui est liée au taux de transfert de chaleur par conduction , domine sans ambiguïté . Cette très grande diffusivité thermique résulte d’une très forte conductivité thermique des métaux, qui est environ 100 fois supérieure à celle de l’eau. Le nombre de Prandtl pour le sodium à une température de fonctionnement typique dans les réacteurs rapides refroidis au sodium est d’environ 0,004. Dans ce cas, le développement de la couche limite thermique est beaucoup plus rapide que celui de la couche limite de vitesse (δ _t >> δ), et il est raisonnable de supposer une vitesse uniforme dans toute la couche limite thermique.

Les coefficients de transfert de chaleur pour le débit de sodium à travers le canal de carburant sont basés sur le nombre de Prandtl et le nombre de Péclet . Le pas au diamètre (P / D) entre également dans de nombreux calculs de transfert de chaleur dans les réacteurs à métal liquide. Les corrélations de transfert de chaleur par convection sont généralement présentées en termes de nombre de Nusselt par rapport au nombre de Péclet . Le nombre typique de Péclet pour un fonctionnement normal est de 150 à 300 dans les grappes de combustible. Comme pour d’autres régimes d’écoulement, le nombre de Nusselt et une corrélation donnée peuvent être utilisés pour déterminer le coefficient de transfert de chaleur par convection.

Exemple – Nombre de Nusselt – Température de surface du revêtement

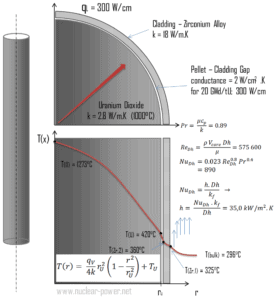Le revêtement est la couche externe des crayons de combustible, se trouvant entre le liquide de refroidissement du réacteur et le combustible nucléaire (c’est-à-dire les pastilles de combustible ). Il est fait d’un matériau résistant à la corrosion avec une faible section d’absorption pour les neutrons thermiques , généralement en alliage de zirconium . Le revêtement empêche les produits de fission radioactifs de s’échapper de la matrice de combustible dans le liquide de refroidissement du réacteur et de le contaminer. Le revêtement constitue l’un des obstacles à l’ approche de « défense en profondeur », donc sa refroidissabilité est l’un des aspects clés de la sécurité.

Considérons la gaine de combustible du rayon intérieur r _{Zr, 2} = 0,408 cm et du rayon extérieur r _{Zr, 1} = 0,465 cm . Par rapport à la pastille de combustible, il n’y a presque pas de génération de chaleur dans la gaine de combustible (la gaine est légèrement chauffée par rayonnement ). Toute la chaleur générée dans le carburant doit être transférée par conduction à travers le revêtement et, par conséquent, la surface intérieure est plus chaude que la surface extérieure.

Suppose que:

• le diamètre extérieur du revêtement est: d = 2 xr _{Zr, 1} = 9,3 mm
• le pas des goupilles de combustible est: p = 13 mm
• la conductivité thermique de l’ eau saturée à 300 ° C est: k _H2O = 0,545 W / mK
• la viscosité dynamique de l’eau saturée à 300 ° C est: μ = 0,0000859 Ns / m ²
• la densité du fluide est: ρ = 714 kg / m ³
• la chaleur spécifique est: c _p = 5,65 kJ / kg.K
• la vitesse d’écoulement du cœur est constante et égale à V _cœur = 5 m / s
• la température du liquide de refroidissement du réacteur à cette coordonnée axiale est: T en _vrac = 296 ° C
• le taux de chaleur linéaire du combustible est q _L = 300 W / cm (F _Q ≈ 2.0) et donc le taux de chaleur volumétrique est q _V = 597 x 10 ⁶ W / m ³

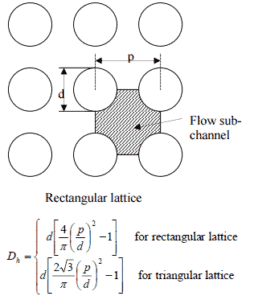Calculez le nombre de Prandtl , Reynolds et Nusselt pour ce régime d’écoulement (écoulement turbulent forcé interne) à l’intérieur du réseau rectangulaire de combustible (canal de combustible), puis calculez le coefficient de transfert de chaleur et enfin la température de surface de la gaine , T _{Zr, 1} .

Pour calculer la température de surface de la gaine , nous devons calculer le nombre de Prandtl , Reynolds et Nusselt , car le transfert de chaleur pour ce régime d’écoulement peut être décrit par l’ équation de Dittus-Boelter , qui est:

Calcul du nombre de Prandtl

Pour calculer le nombre de Prandtl , nous devons savoir:

• la conductivité thermique de l’eau saturée à 300 ° C est: k _H2O = 0,545 W / mK
• la viscosité dynamique de l’eau saturée à 300 ° C est: μ = 0,0000859 Ns / m ²
• la chaleur spécifique est: c _p = 5,65 kJ / kg.K

Notez que tous ces paramètres diffèrent de manière significative pour l’eau à 300 ° C de ceux à 20 ° C. Le nombre de Prandtl pour l’ eau à 20 ° C est d’environ 6,91. Le nombre de Prandtl pour le liquide de refroidissement du réacteur à 300 ° C est alors:

Calcul du nombre de Reynolds

Pour calculer le nombre de Reynolds, nous devons savoir:

• le diamètre extérieur du revêtement est: d = 2 xr _{Zr, 1} = 9,3 mm (pour calculer le diamètre hydraulique)
• le pas des goupilles de combustible est: p = 13 mm  (pour calculer le diamètre hydraulique)
• la viscosité dynamique de l’eau saturée à 300 ° C est: μ = 0,0000859 Ns / m ²
• la densité du fluide est: ρ = 714 kg / m ³

Le diamètre hydraulique, D _h , est un terme couramment utilisé pour gérer le débit dans des tubes et canaux non circulaires . Le diamètre hydraulique du canal de carburant , D _h , est égal à 13,85 mm.

Voir aussi: Diamètre hydraulique

Le nombre de Reynolds à l’intérieur du canal de carburant est alors égal à:

Cela satisfait pleinement les conditions turbulentes .

Calcul du nombre de Nusselt à l’aide de l’équation de Dittus-Boelter

Pour un écoulement turbulent pleinement développé (hydrodynamiquement et thermiquement) dans un tube circulaire lisse, le nombre de Nusselt local peut être obtenu à partir de l’ équation bien connue de Dittus ?? Boelter .

Pour calculer le nombre de Nusselt , nous devons savoir:

• le nombre de Reynolds , qui est Re _Dh = 575600
• le nombre de Prandtl , qui est Pr = 0,89

Le nombre de Nusselt pour la convection forcée à l’intérieur du canal de carburant est alors égal à:

Calcul du coefficient de transfert de chaleur et de la température de surface du revêtement, T _{Zr, 1}

Une connaissance détaillée de la géométrie, des paramètres des fluides, du rayon extérieur du revêtement, du taux de chaleur linéaire, du coefficient de transfert de chaleur par convection nous permet de calculer la différence de température ∆T entre le liquide de refroidissement (T en _vrac ) et la surface du revêtement (T _{Zr, 1} ).

Pour calculer la température de surface de la gaine, il faut savoir:

• le diamètre extérieur du revêtement est: d = 2 x r _{Zr, 1} = 9,3 mm
• le nombre de Nusselt, qui est Nu _Dh = 890
• le diamètre hydraulique du canal de carburant est: D _h = 13,85 mm
• la conductivité thermique du liquide de refroidissement du réacteur (300 ° C) est: k _H2O = 0,545 W / mK
• la température en vrac du liquide de refroidissement du réacteur à cette coordonnée axiale est: T en _vrac = 296 ° C
• le taux de chaleur linéaire du combustible est: q _L = 300 W / cm (F _Q ≈ 2.0)

Le coefficient de transfert de chaleur par convection, h , est donné directement par la définition du nombre de Nusselt:

Enfin, nous pouvons calculer la température de surface de la gaine (T _{Zr, 1} ) simplement en utilisant la loi de Newton du refroidissement :

Pour les REP en fonctionnement normal, il y a une eau liquide comprimée à l’ intérieur du cœur du réacteur, des boucles et des générateurs de vapeur. La pression est maintenue à environ 16 MPa . À cette pression, l’eau bout à environ 350 ° C (662 ° F). Comme on peut le voir, la température de surface T _{Zr, 1} = 325 ° C garantit que même une ébullition sous-refroidie ne se produit pas. Notez que l’ébullition sous-refroidie nécessite T _{Zr, 1} = T _sat . Étant donné que les températures d’entrée de l’eau sont généralement d’environ 290 ° C(554 ° F), il est évident que cet exemple correspond à la partie inférieure du noyau. Aux altitudes plus élevées du cœur, la température globale peut atteindre jusqu’à 330 ° C. La différence de température de 29 ° C peut entraîner une ébullition sous-refroidie (330 ° C + 29 ° C> 350 ° C). D’autre part, l’ ébullition nucléée à la surface perturbe efficacement la couche stagnante et, par conséquent, l’ébullition nucléée augmente considérablement la capacité d’une surface à transférer l’ énergie thermique au fluide en vrac. En conséquence, le coefficient de transfert de chaleur convectif augmente considérablement et donc à des altitudes plus élevées, la différence de température (T _{Zr, 1} – T en _vrac ) diminue considérablement.