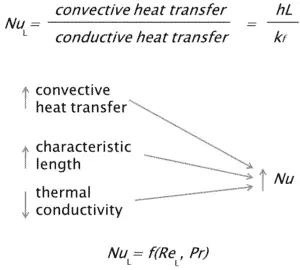
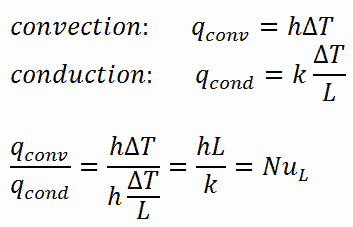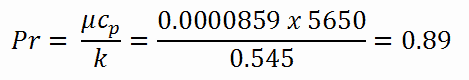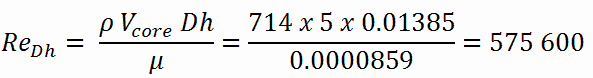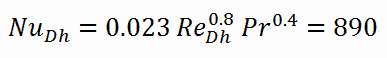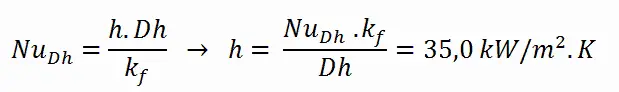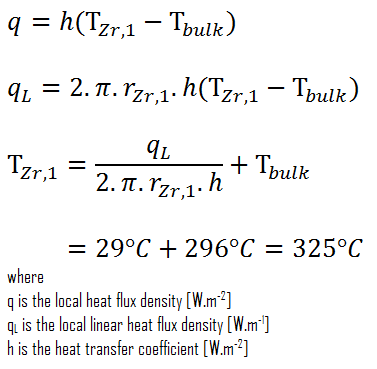Número Nusselt
O número de Nusselt é um número sem dimensão, com o nome de um engenheiro alemão Wilhelm Nusselt. O número de Nusselt está intimamente relacionado ao número de Péclet e os dois números são usados para descrever a proporção da energia térmica convocada para o fluido e a energia térmica conduzida dentro do fluido. O número de Nusselt é igual ao gradiente de temperatura adimensional na superfície e fornece uma medida da transferência de calor por convecção que ocorre na superfície. O componente condutor é medido nas mesmas condições da convecção de calor, mas com um fluido estagnado. O número de Nusselté para a camada limite térmica qual é o coeficiente de atrito para a camada limite de velocidade. Assim, o número de Nusselt é definido como:
Onde:
k f é a condutividade térmica do fluido [W / mK]
L é o comprimento característico
h é o coeficiente de transferência de calor por convecção [W / m 2 .K]
Para ilustração, considere uma camada fluida de espessura L e diferença de temperatura ΔT . A transferência de calor através da camada de fluido será por convecção quando o fluido envolver algum movimento e por condução quando a camada de fluido estiver imóvel.
No caso de condução , o fluxo de calor pode ser calculado usando a lei de condução de Fourier . Em caso de convecção, o fluxo de calor pode ser calculado usando a lei de Newton de resfriamento. Tomando a sua proporção dá:
A equação anterior define o número de Nusselt . Portanto, o número de Nusselt representa o aprimoramento da transferência de calor através de uma camada de fluido como resultado da convecção relativa à condução através da mesma camada de fluido. Um número Nusselt de Nu = 1 para uma camada de fluido representa a transferência de calor através da camada por pura condução . Quanto maior o número de Nusselt , mais eficaz é a convecção. Um número maior de Nusselt corresponde a uma convecção mais eficaz, com fluxo turbulento tipicamente na faixa de 100 a 1000. Para escoamentos turbulentos, o número de Nusselt geralmente é uma função do número de Reynolds e daNúmero Prandtl .
Número de Nusselt para reatores de metais líquidos
Veja também: Número Nusselt para reatores de metais líquidos
Para metais líquidos, o número de Prandtl é muito pequeno, geralmente na faixa de 0,01 a 0,001. Isso significa que a difusividade térmica , que está relacionada à taxa de transferência de calor por condução , domina sem ambiguidade . Essa difusividade térmica muito alta resulta da condutividade térmica muito alta dos metais, que é cerca de 100 vezes maior que a da água. O número de Prandtl para sódio a uma temperatura de operação típica nos reatores rápidos resfriados a sódio é de cerca de 0,004. Nesse caso, o desenvolvimento da camada limite térmica é muito mais rápido que o da camada limite de velocidade (δ t >> δ), e é razoável assumir velocidade uniforme ao longo da camada limite térmica.
Os coeficientes de transferência de calor para o fluxo de sódio através do canal de combustível são baseados no número de Prandtl e no número de Péclet . A inclinação do diâmetro (P / D) também faz muitos cálculos de transferência de calor em reatores de metais líquidos. As correlações convectivas de transferência de calor são geralmente apresentadas em termos de número de Nusselt versus número de Péclet . O número típico de péclet para operação normal é de 150 a 300 nos pacotes de combustível. Quanto a outros regimes de fluxo, o número de Nusselt e uma determinada correlação podem ser usados para determinar o coeficiente de transferência de calor por convecção.
Exemplo – Número de Nusselt – Temperatura da superfície do revestimento
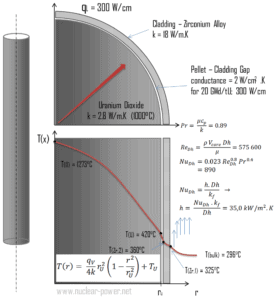 O revestimento é a camada externa das barras de combustível, situada entre o líquido de arrefecimento do reator e o combustível nuclear (isto é, granulados de combustível ). É feito de um material resistente à corrosão com seção transversal de baixa absorção para nêutrons térmicos , geralmente liga de zircônio . O revestimento evita que produtos de fissão radioativa escapem da matriz de combustível para o líquido de arrefecimento do reator e os contaminem. O revestimento constitui uma das barreiras na abordagem de ‘ defesa em profundidade ‘; portanto, sua capacidade de refrigeração é um dos principais aspectos de segurança.
O revestimento é a camada externa das barras de combustível, situada entre o líquido de arrefecimento do reator e o combustível nuclear (isto é, granulados de combustível ). É feito de um material resistente à corrosão com seção transversal de baixa absorção para nêutrons térmicos , geralmente liga de zircônio . O revestimento evita que produtos de fissão radioativa escapem da matriz de combustível para o líquido de arrefecimento do reator e os contaminem. O revestimento constitui uma das barreiras na abordagem de ‘ defesa em profundidade ‘; portanto, sua capacidade de refrigeração é um dos principais aspectos de segurança.
Considere o revestimento de combustível do raio interno r Zr, 2 = 0,408 cm e raio externo r Zr, 1 = 0,465 cm . Em comparação com o pellet de combustível, quase não há geração de calor no revestimento de combustível (o revestimento é levemente aquecido pela radiação ). Todo o calor gerado no combustível deve ser transferido por condução através do revestimento e, portanto, a superfície interna é mais quente que a superfície externa.
Assuma isso:
- o diâmetro externo do revestimento é: d = 2 xr Zr, 1 = 9,3 mm
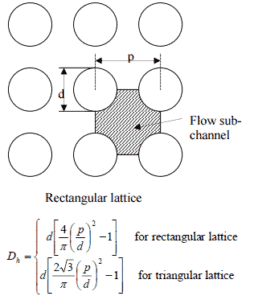
- o passo dos pinos de combustível é: p = 13 mm
- a condutividade térmica da água saturada a 300 ° C é: k H2O = 0,545 W / mK
- a viscosidade dinâmica da água saturada a 300 ° C é: μ = 0,0000859 Ns / m 2
- a densidade do fluido é: ρ = 714 kg / m 3
- o calor específico é: c p = 5,65 kJ / kg.K
- a velocidade de fluxo do núcleo é constante e igual a V core = 5 m / s
- a temperatura do líquido de arrefecimento do reator nesta coordenada axial é: T a granel = 296 ° C
- a taxa linear de calor do combustível é q L = 300 W / cm (F Q ≈ 2.0) e, portanto, a taxa volumétrica de calor é q V = 597 x 10 6 W / m 3
 Calcule o número de Prandtl , Reynolds e Nusselt para esse regime de fluxo (fluxo turbulento forçado interno) dentro da estrutura retangular de combustível (canal de combustível), depois calcule o coeficiente de transferência de calor e, finalmente, a temperatura da superfície do revestimento , T Zr, 1 .
Calcule o número de Prandtl , Reynolds e Nusselt para esse regime de fluxo (fluxo turbulento forçado interno) dentro da estrutura retangular de combustível (canal de combustível), depois calcule o coeficiente de transferência de calor e, finalmente, a temperatura da superfície do revestimento , T Zr, 1 .
Para calcular a temperatura da superfície do revestimento , precisamos calcular o número de Prandtl , Reynolds e Nusselt , porque a transferência de calor para esse regime de fluxo pode ser descrita pela equação de Dittus-Boelter , que é:
Cálculo do número Prandtl
Para calcular o número Prandtl , precisamos saber:
- a condutividade térmica da água saturada a 300 ° C é: k H2O = 0,545 W / mK
- a viscosidade dinâmica da água saturada a 300 ° C é: μ = 0,0000859 Ns / m 2
- o calor específico é: c p = 5,65 kJ / kg.K
Observe que todos esses parâmetros diferem significativamente para a água a 300 ° C daqueles a 20 ° C. O número de prandtl para água a 20 ° C é de cerca de 6,91. O número de Prandtl para o líquido de refrigeração do reator a 300 ° C é então:
Cálculo do número de Reynolds
Para calcular o número de Reynolds, precisamos saber:
- o diâmetro externo do revestimento é: d = 2 xr Zr, 1 = 9,3 mm (para calcular o diâmetro hidráulico)
- o passo dos pinos de combustível é: p = 13 mm (para calcular o diâmetro hidráulico)
- a viscosidade dinâmica da água saturada a 300 ° C é: μ = 0,0000859 Ns / m 2
- a densidade do fluido é: ρ = 714 kg / m 3
O diâmetro hidráulico, D h , é um termo comumente usado ao manipular o fluxo em tubos e canais não circulares . O diâmetro hidráulico do canal de combustível , D h , é igual a 13,85 mm.
Veja também: Diâmetro hidráulico
O número de Reynolds dentro do canal de combustível é então igual a:
Isso satisfaz plenamente as condições turbulentas .
Cálculo do número de Nusselt usando a equação de Dittus-Boelter
Para um fluxo turbulento totalmente desenvolvido (hidrodinamicamente e termicamente) em um tubo circular liso, o número local de Nusselt pode ser obtido a partir da conhecida equação Dittus® Boelter .
Para calcular o número de Nusselt , precisamos saber:
- o número de Reynolds , que é Re Dh = 575600
- o número Prandtl , que é Pr = 0,89
O número de Nusselt para a convecção forçada dentro do canal de combustível é então igual a:
Cálculo do coeficiente de transferência de calor e da temperatura da superfície do revestimento, T Zr, 1
O conhecimento detalhado da geometria, parâmetros do fluido, raio externo do revestimento, taxa de calor linear, coeficiente de transferência de calor por convecção nos permite calcular a diferença de temperatura ∆T entre o líquido de arrefecimento (T a granel ) e a superfície do revestimento (T Zr, 1 ).
Para calcular a temperatura da superfície do revestimento, precisamos saber:
- o diâmetro externo do revestimento é: d = 2 x r Zr, 1 = 9,3 mm
- o número de Nusselt, que é Nu Dh = 890
- o diâmetro hidráulico do canal de combustível é: D h = 13,85 mm
- a condutividade térmica do líquido de refrigeração do reator (300 ° C) é: k H2O = 0,545 W / mK
- a temperatura a granel do líquido de refrigeração do reator nesta coordenada axial é: T a granel = 296 ° C
- a taxa linear de calor do combustível é: q L = 300 W / cm (F Q ≈ 2.0)
O coeficiente de transferência de calor convectivo, h , é dado diretamente pela definição do número de Nusselt:
Finalmente, podemos calcular a temperatura da superfície do revestimento (T Zr, 1 ) simplesmente usando a Lei de Newton de resfriamento :
Para PWRs em operação normal, há água líquida comprimida dentro do núcleo do reator, loops e geradores de vapor. A pressão é mantida em aproximadamente 16MPa . A essa pressão, a água ferve a aproximadamente 350 ° C (662 ° F). Como pode ser visto, a temperatura da superfície T Zr, 1 = 325 ° C garante que mesmo a ebulição sub-resfriada não ocorra. Observe que a ebulição sub-resfriada requer T Zr, 1 = T sat . Como as temperaturas de entrada da água são geralmente de cerca de 290 ° C(554 ° F), é óbvio que este exemplo corresponde à parte inferior do núcleo. Em elevações mais altas do núcleo, a temperatura a granel pode atingir até 330 ° C. A diferença de temperatura de 29 ° C causa a fervura sub-resfriada (330 ° C + 29 ° C> 350 ° C). Por outro lado, a ebulição nucleada na superfície interrompe efetivamente a camada estagnada e, portanto, a ebulição nucleada aumenta significativamente a capacidade de uma superfície de transferir energia térmica para o fluido a granel. Como resultado, o coeficiente de transferência de calor por convecção aumenta significativamente e, portanto, em elevações mais altas, a diferença de temperatura (T Zr, volume 1 – T ) diminui significativamente.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.