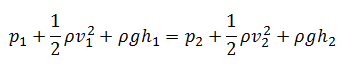Derivación de la ecuación de Bernoulli
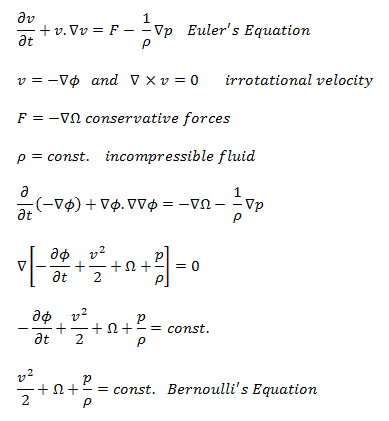La ecuación de Bernoulli para fluidos incompresibles puede derivarse de las ecuaciones de movimiento de Euler bajo restricciones bastante severas.
- La velocidad debe ser derivable de un potencial de velocidad .
- Las fuerzas externas deben ser conservadoras. Es decir, derivable de un potencial.
- La densidad debe ser constante o solo una función de la presión.
- Los efectos térmicos, como la convección natural, se ignoran.
En dinámica de fluidos, las ecuaciones de Euler son un conjunto de ecuaciones hiperbólicas cuasilineales que rigen el flujo adiabático e invisible. Las ecuaciones de Euler se pueden obtener mediante la linealización de estas ecuaciones de Navier-Stokes.
La ecuación de Bernoulli
La ecuación de Bernoulli puede considerarse como una declaración del principio de conservación de energía apropiado para fluidos fluidos. Es una de las ecuaciones más importantes / útiles en mecánica de fluidos . Pone en una relación presión y velocidad en un flujo invisible incompresible . La ecuación de Bernoulli tiene algunas restricciones en su aplicabilidad, se resumen en los siguientes puntos:
- sistema de flujo constante,
- la densidad es constante (lo que también significa que el fluido es incompresible),
- no se realiza ningún trabajo sobre el fluido,
- no se transfiere calor hacia o desde el fluido,
- no ocurre cambio en la energía interna,
- la ecuación relaciona los estados en dos puntos a lo largo de una línea de corriente única (no condiciones en dos líneas de corriente diferentes)
En estas condiciones, la ecuación energética general se simplifica para:
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
