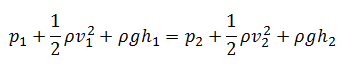Dérivation de l’équation de Bernoulli
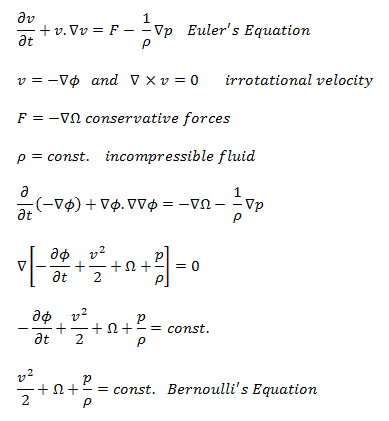L’équation de Bernoulli pour les fluides incompressibles peut être dérivée des équations de mouvement d’ Euler sous des restrictions assez sévères.
- La vitesse doit être dérivée d’un potentiel de vitesse .
- Les forces extérieures doivent être conservatrices. Autrement dit, dérivable d’un potentiel.
- La densité doit être soit constante, soit fonction de la pression seule.
- Les effets thermiques, tels que la convection naturelle, sont ignorés.
En dynamique des fluides, les équations d’Euler sont un ensemble d’équations hyperboliques quasi linéaires régissant le flux adiabatique et inviscide. Les équations d’Euler peuvent être obtenues par linéarisation de ces équations de Navier – Stokes.
L’équation de Bernoulli
L’équation de Bernoulli peut être considérée comme un énoncé du principe de conservation de l’énergie approprié pour les fluides en circulation. C’est l’une des équations les plus importantes / utiles en mécanique des fluides . Il met en relation la pression et la vitesse dans un écoulement incompressible non visqueux . L’équation de Bernoulli a quelques restrictions dans son applicabilité, elles sont résumées dans les points suivants:
- système à débit constant,
- la densité est constante (ce qui signifie également que le fluide est incompressible),
- aucun travail n’est effectué sur ou par le fluide,
- aucune chaleur n’est transférée vers ou depuis le fluide,
- aucun changement ne se produit dans l’énergie interne,
- l’équation relie les états en deux points le long d’une même ligne de courant (pas les conditions sur deux lignes de courant différentes)
Dans ces conditions, l’équation générale de l’énergie est simplifiée pour:
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
