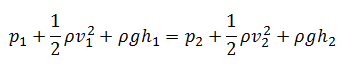Derivação da equação de Bernoulli
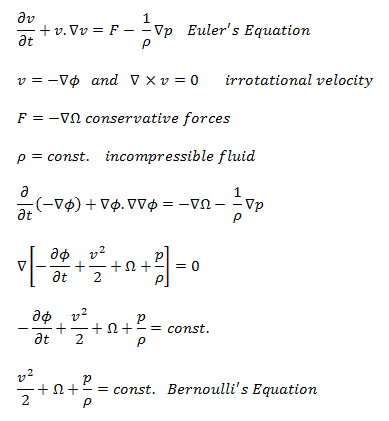A equação de Bernoulli para fluidos incompressíveis pode ser derivada das equações de movimento de Euler sob restrições bastante severas.
- A velocidade deve ser derivada de um potencial de velocidade .
- Forças externas devem ser conservadoras. Ou seja, derivável de um potencial.
- A densidade deve ser constante ou apenas uma função da pressão.
- Efeitos térmicos, como convecção natural, são ignorados.
Na dinâmica de fluidos, as equações de Euler são um conjunto de equações hiperbólicas quaseilineares que governam o fluxo adiabático e invíscido. As equações de Euler podem ser obtidas pela linearização dessas equações de Navier-Stokes.
quação de Bernoulli
A equação de Bernoulli pode ser considerada uma afirmação do princípio de conservação de energia apropriado para fluidos fluidos. É uma das equações mais importantes / úteis na mecânica de fluidos . Ele coloca em uma relação pressão e velocidade em um fluxo incompreensível inviscível . A equação de Bernoulli tem algumas restrições em sua aplicabilidade, resumidas nos seguintes pontos:
- sistema de fluxo constante,
- a densidade é constante (o que também significa que o fluido é incompressível),
- nenhum trabalho é feito sobre ou pelo fluido,
- nenhum calor é transferido para ou a partir do fluido,
- nenhuma mudança ocorre na energia interna,
- a equação relaciona os estados em dois pontos ao longo de uma única linha de fluxo (não condições em duas linhas de fluxo diferentes)
Sob essas condições, a equação geral de energia é simplificada para:
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
