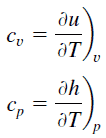Energía interna de un gas ideal
La energía interna es el total de toda la energía asociada con el movimiento de los átomos o moléculas en el sistema. Las formas microscópicas de energía incluyen aquellas debidas a la rotación , vibración , traslación e interacciones entre las moléculas de una sustancia.
Gas monoatómico – Energía interna
Para un gas ideal monoatómico (como helio, neón o argón), la única contribución a la energía proviene de la energía cinética traslacional . La energía cinética traslacional promedio de un solo átomo depende solo de la temperatura del gas y está dada por la ecuación:
K promedio = 3/2 kT.
La energía interna de n moles de un gas monoatómico ideal (un átomo por molécula) es igual a la energía cinética promedio por molécula multiplicada por el número total de moléculas, N:
E int = 3/2 NkT = 3/2 nRT
donde n es el número de moles. Cada dirección (x, y y z) contribuye (1/2) nRT a la energía interna . Aquí es donde entra en juego la idea de equipartición de energía : cualquier otra contribución a la energía también debe contribuir (1/2) nRT . Como se puede ver, la energía interna de un gas ideal depende solo de la temperatura y la cantidad de moles de gas.
Molécula Diatómica – Energía Interna
Si las moléculas de gas contienen más de un átomo, hay tres direcciones de traslación , y la energía cinética rotacional también contribuye, pero solo para rotaciones de dos de los tres ejes perpendiculares. Las cinco contribuciones a la energía (cinco grados de libertad) dan:
Gas ideal diatómico:
E int = 5/2 NkT = 5/2 nRT
Esto es solo una aproximación y se aplica a temperaturas intermedias. A bajas temperaturas solo contribuye la energía cinética traslacional , y a temperaturas más altas dos vibraciones aportan dos contribuciones adicionales (energía cinética y potencial). La energía interna será mayor a una temperatura dada que para un gas monoatómico, pero seguirá siendo función solo de la temperatura para un gas ideal.
La energía interna de los gases reales también depende principalmente de la temperatura, pero de manera similar a la Ley del Gas Ideal , la energía interna de los gases reales también depende en cierta medida de la presión y el volumen . Todos los gases reales se aproximan al estado ideal a bajas presiones (densidades). A bajas presiones, las moléculas están lo suficientemente separadas como para que no interactúen entre sí. La energía interna de líquidos y sólidos es bastante complicada, ya que incluye la energía potencial eléctrica asociada con las fuerzas (o enlaces químicos ) entre átomos y moléculas.
Calor específico a volumen constante y presión constante
El calor específico es una propiedad relacionada con la energía interna que es muy importante en termodinámica. Las propiedades intensivas c v y c p se definen para sustancias compresibles puras y simples como derivadas parciales de la energía interna u (T, v) y entalpía h (T, p) , respectivamente:
donde los subíndices v y p denotan las variables mantenidas fijas durante la diferenciación. Las propiedades c v y c p se denominan calores específicos (o capacidades de calor ) porque, bajo ciertas condiciones especiales, relacionan el cambio de temperatura de un sistema con la cantidad de energía agregada por la transferencia de calor. Sus unidades SI son J / kg K o J / mol K . Se definen dos calores específicos para gases, uno para volumen constante (c v ) y otro para presión constante (c p ) .
Según la primera ley de la termodinámica , para un proceso de volumen constante con un gas ideal monoatómico, el calor específico molar será:
C v = 3 / 2R = 12.5 J / mol K
porque
U = 3 / 2nRT
Se puede deducir que el calor específico molar a presión constante es:
C p = C v + R = 5 / 2R = 20.8 J / mol K
Este C p es mayor que el calor específico molar a volumen constante C v , porque ahora se debe suministrar energía no solo para elevar la temperatura del gas sino también para que el gas funcione porque en este caso el volumen cambia.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
