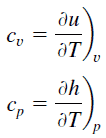Energie interne d’un gaz parfait
L’ énergie interne est le total de toute l’énergie associée au mouvement des atomes ou des molécules dans le système. Les formes d’énergie microscopiques incluent celles dues à la rotation , à la vibration , à la translation et aux interactions entre les molécules d’une substance.
Monatomic Gas – Energie interne
Pour un gaz parfait monoatomique (tel que l’hélium, le néon ou l’argon), la seule contribution à l’énergie provient de l’énergie cinétique de translation . L’énergie cinétique de translation moyenne d’un seul atome dépend uniquement de la température du gaz et est donnée par l’équation:
K moy = 3/2 kT.
L’énergie interne de n moles d’un gaz monatomique idéal (un atome par molécule) est égale à l’énergie cinétique moyenne par molécule fois le nombre total de molécules, N:
E int = 3/2 NkT = 3/2 nRT
où n est le nombre de moles. Chaque direction (x, y et z) contribue (1/2) nRT à l’ énergie interne . C’est là que l’ équipartition de l’idée énergétique entre en jeu – toute autre contribution à l’énergie doit également contribuer (1/2) nRT . Comme on peut le constater, l’énergie interne d’un gaz parfait ne dépend que de la température et du nombre de moles de gaz.
Molécule Diatomique – Energie Interne
Si les molécules de gaz contiennent plus d’un atome, il existe trois directions de translation et une énergie cinétique de rotation y contribue également, mais uniquement pour les rotations autour de deux des trois axes perpendiculaires. Les cinq contributions à l’énergie (cinq degrés de liberté) donnent:
Gaz idéal diatomique:
E int = 5/2 NkT = 5/2 nRT
Ceci n’est qu’une approximation et s’applique aux températures intermédiaires. Aux basses températures, seule l’ énergie cinétique de translation contribue , et à des températures plus élevées, deux contributions supplémentaires (énergie cinétique et potentielle) proviennent des vibrations. L’ énergie interne sera plus grande à une température donnée que pour un gaz monoatomique, mais elle ne restera fonction que de la température pour un gaz parfait.
L’énergie interne des gaz réels dépend également principalement de la température, mais de la même manière que la loi des gaz parfaits , l’énergie interne des gaz réels dépend également quelque peu de la pression et du volume . Tous les gaz réels approchent de l’état idéal à de faibles pressions (densités). A basse pression, les molécules sont suffisamment éloignées pour ne pas interagir les unes avec les autres. L’énergie interne des liquides et des solides est assez compliquée, car elle comprend l’énergie potentielle électrique associée aux forces (ou liaisons chimiques ) entre les atomes et les molécules.
Chaleur spécifique à volume et pression constants
La chaleur spécifique est une propriété liée à l’énergie interne qui est très importante en thermodynamique. Les propriétés intensives c v et c p sont définies pour les substances compressibles pures et simples comme des dérivées partielles de l’ énergie interne u (T, v) et de l’ enthalpie h (T, p) , respectivement:
où les indices v et p désignent les variables maintenues fixes pendant la différenciation. Les propriétés c v et c p sont appelées chaleurs spécifiques (ou capacités calorifiques ) car dans certaines conditions particulières, elles relient le changement de température d’un système à la quantité d’énergie ajoutée par transfert de chaleur. Les unités SI sont J / kg K ou J / mole K . Deux chaleurs spécifiques sont définies pour les gaz, une pour un volume constant (c v ) et une pour une pression constante (c p ) .
Selon la première loi de la thermodynamique , pour un procédé à volume constant avec un gaz parfait monatomique, la chaleur spécifique molaire sera:
C v = 3 / 2R = 12,5 J / mol K
car
U = 3 / 2nRT
On peut déduire que la chaleur spécifique molaire à pression constante est:
C p = C v + R = 5 / 2R = 20,8 J / mol K
Ce C p est supérieur à la chaleur spécifique molaire à volume constant C v , car il faut désormais fournir de l’énergie non seulement pour élever la température du gaz mais aussi pour que le gaz fonctionne car dans ce cas le volume change.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
