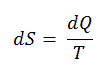¿Qué es la entalpía?
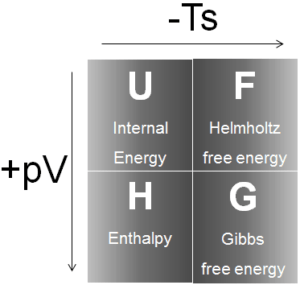
En termodinámica, la entalpía es la medida de energía en un sistema termodinámico. Es la cantidad termodinámica equivalente al contenido de calor total de un sistema. La entalpía se define como la suma de la energía interna E más el producto de la presión py el volumen V. En muchos análisis termodinámicos aparece la suma de la energía interna U y el producto de la presión py el volumen V, por lo tanto, es conveniente para dar a la combinación un nombre, entalpía y un símbolo distintivo, H.
La entalpía es la expresión preferida de los cambios de energía del sistema en muchas mediciones químicas, biológicas y físicas a presión constante . Es tan útil que está tabulado en las tablas de vapor junto con un volumen específico y una energía interna específica . Es debido al hecho, simplifica la descripción de la transferencia de energía . A presión constante, el cambio de entalpía es igual a la energía transferida desde el medio ambiente a través del calentamiento (Q = H 2 – H 1 ) u otro trabajo que no sea el trabajo de expansión. Para un proceso de presión variable, la diferencia en entalpía no es tan obvia.
Entalpía en unidades extensas
H = U + pV
La entalpía es una cantidad extensa, depende del tamaño del sistema o de la cantidad de sustancia que contiene. La unidad de entalpía del SI es el joule (J). Es la energía contenida dentro del sistema, excluyendo la energía cinética de movimiento del sistema como un todo y la energía potencial del sistema como un todo debido a los campos de fuerza externos. Es la cantidad termodinámica equivalente al contenido de calor total de un sistema.
Por otro lado, la energía puede almacenarse en los enlaces químicos entre los átomos que forman las moléculas. Este almacenamiento de energía a nivel atómico incluye energía asociada con estados orbitales de electrones, espín nuclear y fuerzas de unión en el núcleo.
La entalpía está representada por el símbolo H , y el cambio en la entalpía en un proceso es H 2 – H 1 .
Hay expresiones en términos de variables más familiares como temperatura y presión :
dH = C p dT + V (1-αT) dp
Donde C p es la capacidad calorífica a presión constante y α es el coeficiente de expansión térmica (cúbica). Para gas ideal αT = 1 y por lo tanto:
dH = C p dT
Ejemplo: Pistón sin fricción – Calor – Entalpía
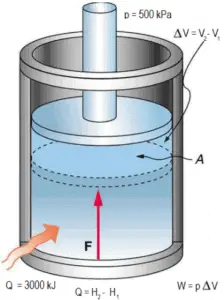
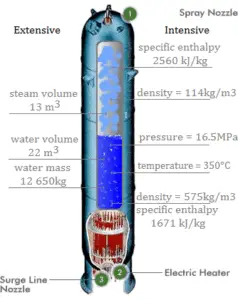
Un pistón sin fricción se utiliza para proporcionar una presión constante de 500 kPa en un cilindro que contiene vapor de agua ( vapor sobrecalentado ) de un volumen de 2 m 3 a 500 K . Calcule la temperatura final, si se agregan 3000 kJ de calor .
Solución:
Usando tablas de vapor , sabemos que la entalpía específica de dicho vapor (500 kPa; 500 K) es de aproximadamente 2912 kJ / kg . Como en esta condición el vapor tiene una densidad de 2.2 kg / m 3 , entonces sabemos que hay alrededor de 4.4 kg de vapor en el pistón a una entalpía de 2912 kJ / kg x 4.4 kg = 12812 kJ .
Cuando usamos simplemente Q = H 2 – H 1 , la entalpía de vapor resultante será:
H 2 = H 1 + Q = 15812 kJ
De las mesas de vapor , dicho vapor sobrecalentado (15812 / 4.4 = 3593 kJ / kg) tendrá una temperatura de 828 K (555 ° C) . Dado que en esta entalpía el vapor tiene una densidad de 1.31 kg / m 3 , es obvio que se ha expandido aproximadamente 2.2 / 1.31 = 1.67 (+ 67%). Por lo tanto, el volumen resultante es 2 m 3 x 1.67 = 3.34 m 3 y ∆V = 3.34 m 3 – 2 m 3 = 1.34 m 3 .
La parte p∆V de la entalpía, es decir, el trabajo realizado es:
W = p∆V = 500 000 Pa x 1.34 m 3 = 670 kJ
¿Qué es la entropía?
En termodinámica y física estadística, la entropía es una medida cuantitativa del desorden, o de la energía en un sistema para hacer el trabajo.
En física estadística, la entropía es una medida del desorden de un sistema. A lo que se refiere el trastorno es realmente el número de configuraciones microscópicas , W , que puede tener un sistema termodinámico cuando está en un estado especificado por ciertas variables macroscópicas ( volumen , energía , presión y temperatura ). Por “estados microscópicos”, nos referimos a los estados exactos de todas las moléculas que componen el sistema.
Matemáticamente, la definición exacta es:
Entropía = (constante de Boltzmann k) x logaritmo del número de estados posibles
S = k B logW
Esta ecuación, que relaciona los detalles microscópicos, o microestados, del sistema (a través de W ) con su estado macroscópico (a través de la entropía S ), es la idea clave de la mecánica estadística. En un sistema cerrado, la entropía nunca disminuye, por lo que en el Universo la entropía aumenta irreversiblemente. En un sistema abierto (por ejemplo, un árbol en crecimiento), la entropía puede disminuir y el orden puede aumentar, pero solo a expensas de un aumento de la entropía en otro lugar (por ejemplo, en el Sol).
Unidades de entropía
El SI unidad para la entropía es J / K . Según Clausius, la entropía se definió mediante el cambio en la entropía S de un sistema. El cambio en la entropía S, cuando se le agrega una cantidad de calor Q mediante un proceso reversible a temperatura constante, viene dado por:
Aquí Q es la energía transferida como calor hacia o desde el sistema durante el proceso, y T es la temperatura del sistema en grados Kelvin durante el proceso. Si suponemos un proceso isotérmico reversible , el cambio de entropía total viene dado por:
∆S = S 2 – S 1 = Q / T
En esta ecuación, el cociente Q / T está relacionado con el aumento del desorden. Mayor temperatura significa mayor aleatoriedad de movimiento. A temperaturas más bajas, la adición de calor Q provoca un aumento fraccional sustancial en el movimiento molecular y la aleatoriedad. Por otro lado, si la sustancia ya está caliente, la misma cantidad de calor Q agrega relativamente poco al mayor movimiento molecular.
Ejemplo
Calcule el cambio en la entropía de 1 kg de hielo a 0 ° C, cuando se derrite reversiblemente en agua a 0 ° C.
Dado que es un proceso isotérmico, podemos usar:
∆S = S 2 – S 1 = Q / T
por lo tanto, el cambio de entropía será:
∆S = 334 [kJ] / 273.15 [K] = 1.22 [kJ / K]
donde se requieren 334 kilojulios de calor para derretir 1 kg de hielo (calor de fusión latente = 334 kJ / kg) y este calor se transfiere al sistema a 0 ° C (273,15 K).
Diagramas Ts
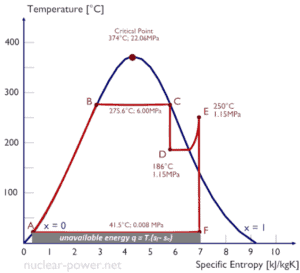
En general, las fases de una sustancia y las relaciones entre sus propiedades se muestran más comúnmente en los diagramas de propiedades . Se ha definido una gran cantidad de propiedades diferentes y existen algunas dependencias entre las propiedades.
Un diagrama de temperatura-entropía ( diagrama Ts ) es el tipo de diagrama más utilizado para analizar los ciclos del sistema de transferencia de energía. Se utiliza en termodinámica para visualizar cambios en la temperatura y entropía específica durante un proceso o ciclo termodinámico.
Esto se debe a que el trabajo realizado por o en el sistema y el calor agregado o eliminado del sistema se pueden visualizar en el diagrama Ts . Según la definición de entropía, el calor transferido hacia o desde un sistema es igual al área bajo la curva Ts del proceso.
dQ = TdS
Un proceso isentrópico se representa como una línea vertical en un diagrama Ts, mientras que un proceso isotérmico es una línea horizontal. En un estado idealizado, la compresión es una bomba, la compresión en un compresor y la expansión en una turbina son procesos isoentrópicos. Por lo tanto, es muy útil en ingeniería de energía, porque estos dispositivos se usan en ciclos termodinámicos de plantas de energía.
Tenga en cuenta que los supuestos isentrópicos solo son aplicables con ciclos ideales. Los ciclos termodinámicos reales tienen pérdidas de energía inherentes debido a la ineficiencia de los compresores y las turbinas.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.