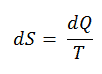What is Enthalpy
In thermodynamics, the enthalpy is the measure of energy in a thermodynamic system. It is the thermodynamic quantity equivalent to the total heat content of a system. The enthalpy is defined to be the sum of the internal energy E plus the product of the pressure p and volume V. In many thermodynamic analyses the sum of the internal energy U and the product of pressure p and volume V appears, therefore it is convenient to give the combination a name, enthalpy, and a distinct symbol, H.
The enthalpy is the preferred expression of system energy changes in many chemical, biological, and physical measurements at constant pressure. It is so useful that it is tabulated in the steam tables along with specific volume and specific internal energy. It is due to the fact, it simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating (Q = H2 – H1) or work other than expansion work. For a variable-pressure process, the difference in enthalpy is not quite as obvious.
Enthalpy in Extensive Units
H = U + pV
Enthalpy is an extensive quantity, it depends on the size of the system, or on the amount of substance it contains. The SI unit of enthalpy is the joule (J). It is the energy contained within the system, excluding the kinetic energy of motion of the system as a whole and the potential energy of the system as a whole due to external force fields. It is the thermodynamic quantity equivalent to the total heat content of a system.
On the other hand, energy can be stored in the chemical bonds between the atoms that make up the molecules. This energy storage on the atomic level includes energy associated with electron orbital states, nuclear spin, and binding forces in the nucleus.
Enthalpy is represented by the symbol H, and the change in enthalpy in a process is H2 – H1.
There are expressions in terms of more familiar variables such as temperature and pressure:
dH = CpdT + V(1-αT)dp
Where Cp is the heat capacity at constant pressure and α is the coefficient of (cubic) thermal expansion. For ideal gas αT = 1 and therefore:
dH = CpdT
Example: Frictionless Piston – Heat – Enthalpy
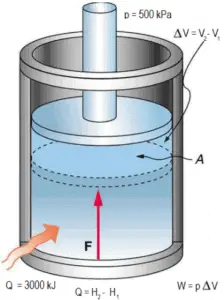
A frictionless piston is used to provide a constant pressure of 500 kPa in a cylinder containing steam (superheated steam) of a volume of 2 m3 at 500 K. Calculate the final temperature, if 3000 kJ of heat is added.
Solution:
Using steam tables we know, that the specific enthalpy of such steam (500 kPa; 500 K) is about 2912 kJ/kg. Since at this condition the steam has density of 2.2 kg/m3, then we know there is about 4.4 kg of steam in the piston at enthalpy of 2912 kJ/kg x 4.4 kg = 12812 kJ.
When we use simply Q = H2 − H1, then the resulting enthalpy of steam will be:
H2 = H1 + Q = 15812 kJ
From steam tables, such superheated steam (15812/4.4 = 3593 kJ/kg) will have a temperature of 828 K (555°C). Since at this enthalpy the steam have density of 1.31 kg/m3, it is obvious that it has expanded by about 2.2/1.31 = 1.67 (+67%). Therefore the resulting volume is 2 m3 x 1.67 = 3.34 m3 and ∆V = 3.34 m3 – 2 m3 = 1.34 m3.
The p∆V part of enthalpy, i.e. the work done is:
W = p∆V = 500 000 Pa x 1.34 m3 = 670 kJ
What is Entropy
In thermodynamics and statistical physics, entropy is a quantitative measure of disorder, or of the energy in a system to do work.
In statistical physics, entropy is a measure of the disorder of a system. What disorder refers to is really the number of microscopic configurations, W, that a thermodynamic system can have when in a state as specified by certain macroscopic variables (volume, energy, pressure, and temperature). By “microscopic states”, we mean the exact states of all the molecules making up the system.
Mathematically, the exact definition is:
Entropy = (Boltzmann’s constant k) x logarithm of number of possible states
S = kB logW
This equation, which relates the microscopic details, or microstates, of the system (via W) to its macroscopic state (via the entropy S), is the key idea of statistical mechanics. In a closed system, entropy never decreases, so in the Universe entropy is irreversibly increasing. In an open system (for example, a growing tree), entropy can decrease and order can increase, but only at the expense of an increase in entropy somewhere else (e.g. in the Sun).
Units of Entropy
The SI unit for entropy is J/K. According to Clausius, the entropy was defined via the change in entropy S of a system. The change in entropy S, when an amount of heat Q is added to it by a reversible process at constant temperature, is given by:
Here Q is the energy transferred as heat to or from the system during the process, and T is the temperature of the system in kelvins during the process. If we assume a reversible isothermal process, the total entropy change is given by:
∆S = S2 – S1 = Q/T
In this equation the quotient Q/T is related to the increase in disorder. Higher temperature means greater randomness of motion. At lower temperatures adding heat Q causes a substantial fractional increase in molecular motion and randomness. On the other hand if the substance is already hot, the same quantity of heat Q adds relatively little to the greater molecular motion.
Example
Calculate the change in entropy of 1 kg of ice at 0°C, when melted reversibly to water at 0°C.
Since it is an isothermal process, we can use:
∆S = S2 – S1 = Q/T
therefore the entropy change will be:
∆S = 334 [kJ] / 273.15 [K] = 1.22 [kJ/K]
where 334 kilojoules of heat are required to melt 1 kg of ice (latent heat of fusion = 334 kJ/kg) and this heat is transferred to the system at 0°C (273.15 K).
T-s Diagrams
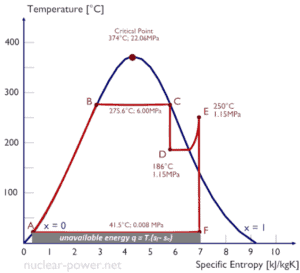
In general, the phases of a substance and the relationships between its properties are most commonly shown on property diagrams. A large number of different properties have been defined, and there are some dependencies between properties.
A Temperature-entropy diagram (T-s diagram) is the type of diagram most frequently used to analyze energy transfer system cycles. It is used in thermodynamics to visualize changes to temperature and specific entropy during a thermodynamic process or cycle.
This is because the work done by or on the system and the heat added to or removed from the system can be visualized on the T-s diagram. By the definition of entropy, the heat transferred to or from a system equals the area under the T-s curve of the process.
dQ = TdS
An isentropic process is depicted as a vertical line on a T-s diagram, whereas an isothermal process is a horizontal line. In an idealized state, compression is a pump, compression in a compressor and expansion in a turbine are isentropic processes. Therefore it is very useful in power engineering, because these devices are used in thermodynamic cycles of power plants.
Note that, the isentropic assumptions are only applicable with ideal cycles. Real thermodynamic cycles have inherent energy losses due to inefficiency of compressors and turbines.
We hope, this article, Enthalpy and Entropy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.