La loi de la conservation de la matière – Conservation de la masse
La loi de la conservation de la matière ou le principe de la conservation de la matière stipule que la masse d’un objet ou d’une collection d’objets ne change jamais avec le temps, quelle que soit la manière dont les parties constitutives se réarrangent.
La masse ne peut être ni créée ni détruite.
La loi exige que, lors d’une réaction nucléaire , d’une désintégration radioactive ou d’ une réaction chimique dans un système isolé, la masse totale des réactifs ou des matières de départ soit égale à la masse des produits .
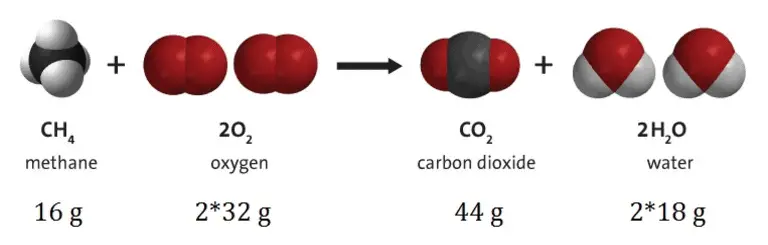 Historiquement, les anciens Grecs ont déjà proposé l’idée que la quantité totale de matière dans l’univers est constante . Le principe de conservation de la masse a été défini pour la première fois par Mikhail Lomonosov en 1748. Cependant, la loi de conservation de la matière (ou principe de conservation de la masse / matière ) en tant que principe fondamental de la physique a été découverte par Antoine Lavoisier à la fin du XVIIIe siècle. . Il était très important de passer de l’alchimie à la chimie moderne . Avant cette découverte, il y avait des questions comme:
Historiquement, les anciens Grecs ont déjà proposé l’idée que la quantité totale de matière dans l’univers est constante . Le principe de conservation de la masse a été défini pour la première fois par Mikhail Lomonosov en 1748. Cependant, la loi de conservation de la matière (ou principe de conservation de la masse / matière ) en tant que principe fondamental de la physique a été découverte par Antoine Lavoisier à la fin du XVIIIe siècle. . Il était très important de passer de l’alchimie à la chimie moderne . Avant cette découverte, il y avait des questions comme:
- Pourquoi un morceau de bois pèse moins après avoir brûlé?
- Une matière ou une partie de celle-ci peut-elle disparaître?
Dans le cas du bois brûlé, le problème était la mesure du poids des gaz libérés . La mesure du poids des gaz libérés était compliquée à cause de l’ effet de flottabilité de l’atmosphère terrestre sur le poids des gaz. Une fois comprise, la conservation de la matière revêtait une importance cruciale dans le passage de l’alchimie à la science naturelle moderne de la chimie.
La loi de conservation de la matière dans la théorie de la relativité restreinte
Au début du XXe siècle, la notion de masse subit une révision radicale. La masse a perdu son absolu . L’un des résultats frappants de la théorie de la relativité d’Einstein est que la masse et l’énergie sont équivalentes et convertibles l’ une en l’autre. L’équivalence de la masse et de l’énergie est décrite par la célèbre formule d’Einstein E = mc 2 . En mots, l’ énergie est égale à la masse multipliée par la vitesse de la lumière au carré. Parce que la vitesse de la lumière est un très grand nombre, la formule implique que toute petite quantité de matière contient une très grande quantité d’énergie. La masse d’un objet était considérée comme équivalente à l’énergie, interconvertible avec l’énergie et augmentant considérablement à des vitesses extrêmement élevées proches de celles de la lumière. L’ énergie totale d’un objet était comprise comme comprenant sa masse au repos ainsi que son augmentation de masse causée par l’ augmentation de l’énergie cinétique .
Dans la théorie spéciale de la relativité, certains types de matière peuvent être créés ou détruits , mais dans tous ces processus, la masse et l’énergie associées à une telle matière restent inchangées en quantité . Il a été constaté que la masse au repos d’un noyau atomique est sensiblement plus petite que la somme des masses au repos de ses protons, neutrons et électrons constitutifs . La masse n’était plus considérée comme immuable dans le système fermé. La différence est une mesure de l’ énergie de liaison nucléaire qui maintient le noyau ensemble. Selon la relation d’Einstein ( E = mc 2 ), cette énergie de liaison est proportionnelle à cette différence de masse et elle est connue sous le nom de défaut de masse .
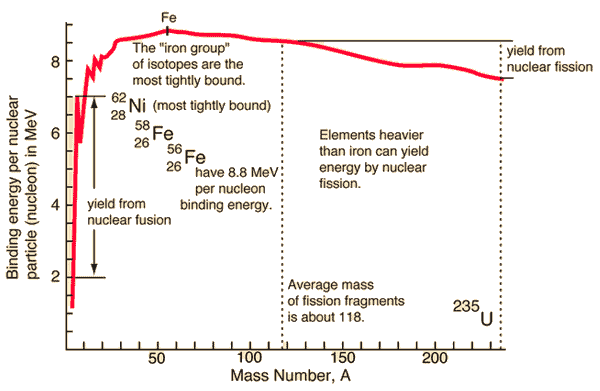
Source: hyperphysics.phy-astr.gsu.edu
Lors de la scission nucléaire ou de la fusion nucléaire , une partie de la masse du noyau est convertie en énormes quantités d’énergie et ainsi cette masse est retirée de la masse totale des particules d’origine, et la masse manque dans le noyau résultant. Les énergies de liaison nucléaire sont énormes, elles sont de l’ordre d’un million de fois supérieures aux énergies de liaison électronique des atomes.
Généralement, dans les réactions chimiques et nucléaires , une certaine conversion entre la masse au repos et l’énergie se produit, de sorte que les produits ont généralement une masse plus petite ou plus grande que les réactifs. Par conséquent, le nouveau principe de conservation est la conservation de l’énergie de masse .
Voir aussi: Libération d’énergie de la fission
La loi de conservation de la matière en dynamique des fluides
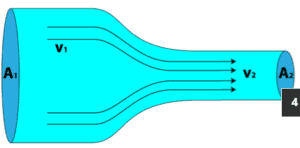
Ce principe est généralement connu sous le nom de principe de conservation de la matière et stipule que la masse d’un objet ou d’une collection d’objets ne change jamais avec le temps, quelle que soit la façon dont les parties constitutives se réorganisent. Ce principe peut être utilisé dans l’analyse des fluides en circulation . La conservation de la masse dans la dynamique des fluides indique que tous les débits massiques dans un volume de contrôle sont égaux à tous les débits massiques hors du volume de contrôle plus le taux de changement de masse dans le volume de contrôle. Ce principe est exprimé mathématiquement par l’équation suivante:
ṁ in = ṁ out + ∆m ⁄ ∆t
Masse entrant par unité de temps = Masse quittant par unité de temps + Augmentation de la masse du volume de contrôle par unité de temps

Cette équation décrit le flux non stationnaire . L’écoulement en régime non permanent fait référence à la condition dans laquelle les propriétés du fluide à un point unique du système peuvent changer au fil du temps. L’écoulement en régime permanent fait référence à la condition dans laquelle les propriétés du fluide ( température, pression et vitesse ) à un point unique du système ne changent pas avec le temps . Mais l’une des propriétés les plus importantes qui est constante dans un système de flux en régime permanent est le débit massique du système. Cela signifie qu’il n’y a pas d’accumulation de masse dans aucun composant du système.
Voir aussi: Équation de continuité
Équation de continuité
L’ équation de continuité est simplement une expression mathématique du principe de conservation de la masse. Pour un volume de contrôle qui a une seule entrée et une seule sortie , le principe de conservation de la masse stipule que, pour un débit en régime permanent , le débit massique dans le volume doit être égal au débit massique sortant.
ṁ in = ṁ out
Masse entrant par unité de temps = Masse sortant par unité de temps
Cette équation est appelée équation de continuité pour un écoulement unidimensionnel stable. Pour un débit constant à travers un volume de contrôle avec de nombreuses entrées et sorties, le débit massique net doit être nul, où les entrées sont négatives et les sorties sont positives.
Ce principe peut être appliqué à un streamtube tel que celui illustré ci-dessus. Aucun fluide ne s’écoule à travers la limite créée par les lignes de courant, de sorte que la masse entre et sort uniquement par les deux extrémités de cette section de tube de courant.
Lorsqu’un fluide est en mouvement, il doit se déplacer de manière à conserver la masse. Pour voir comment la conservation de la masse impose des restrictions sur le champ de vitesse, considérez l’écoulement régulier de fluide à travers un conduit (c’est-à-dire que les débits d’entrée et de sortie ne varient pas avec le temps).
Forme différentielle d’équation de continuité
Une équation générale de continuité peut également s’écrire sous une forme différentielle :
∂⍴ ⁄ ∂t + ∇. (⍴ ͞v) = σ
où
- ∇. est la divergence,
- ρ est la densité de la quantité q,
- ⍴ ͞v est le flux de quantité q,
- σ est la génération de q par unité de volume par unité de temps. Les termes qui génèrent (σ> 0) ou suppriment (σ <0) q sont appelés respectivement «sources» et «puits». Si q est une quantité conservée (telle que l’énergie), σ est égal à 0.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
