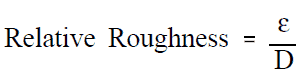Rugosité relative
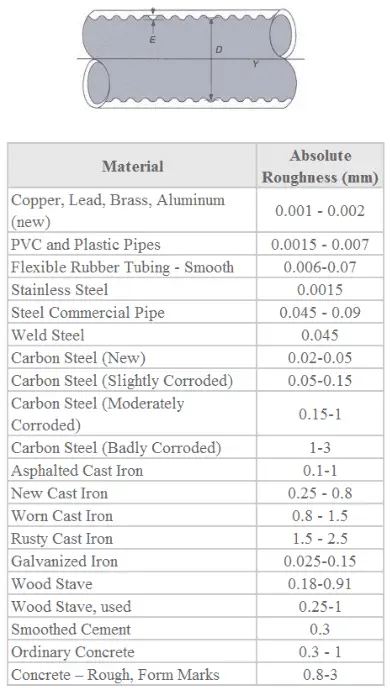
La quantité utilisée pour mesurer la rugosité de la surface intérieure du tuyau est appelée rugosité relative , et elle est égale à la hauteur moyenne des irrégularités de surface (ε) divisée par le diamètre du tuyau (D).
, où les irrégularités de surface de hauteur moyenne et le diamètre du tuyau sont exprimés en millimètres.
Si nous connaissons la rugosité relative de la surface intérieure du tuyau, nous pouvons obtenir la valeur du facteur de friction à partir du diagramme de Moody .
Le diagramme de Moody (également connu sous le nom de diagramme de Moody) est un graphique sous forme non dimensionnelle qui met en relation le facteur de friction Darcy , le nombre de Reynolds et la rugosité relative pour un écoulement pleinement développé dans un tuyau circulaire.
Sommaire:
- La perte de charge du système hydraulique est divisée en deux catégories principales :
- Perte de charge importante – due au frottement dans des tuyaux droits
- Perte de charge mineure – due à des composants comme des valves, des coudes…
- L’équation de Darcy peut être utilisée pour calculer les pertes majeures .
- Le facteur de friction pour l’écoulement du fluide peut être déterminé à l’aide d’un diagramme de Moody .
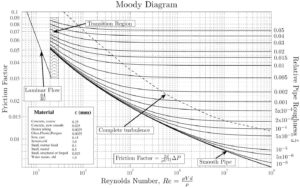
- Le facteur de friction pour l’écoulement laminaire est indépendant de la rugosité de la surface intérieure du tuyau. f = 64 / Re
- Le facteur de frottement pour un écoulement turbulent dépend fortement de la rugosité relative . Elle est déterminée par l’équation de Colebrook. Il faut noter qu’aux très grands nombres de Reynolds , le facteur de friction est indépendant du nombre de Reynolds.
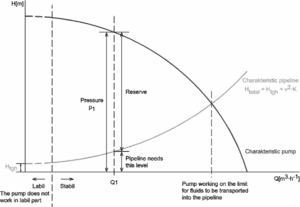
Pourquoi la perte de tête est très importante?
Comme on peut le voir sur la photo, la perte de charge est une caractéristique clé de tout système hydraulique. Dans les systèmes dans lesquels un certain débit doit être maintenu (par exemple pour assurer un refroidissement ou un transfert de chaleur suffisant à partir d’un cœur de réacteur ), l’équilibre de la perte de charge et de la tête ajoutée par une pompe détermine le débit à travers le système.
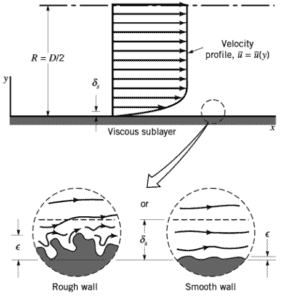Il faut noter qu’aux très grands nombres de Reynolds , le facteur de friction est indépendant du nombre de Reynolds . En effet, l’épaisseur de la sous-couche laminaire (sous-couche visqueuse) diminue avec l’augmentation du nombre de Reynolds. Pour les très grands nombres de Reynolds, l’épaisseur de la sous-couche laminaire est comparable à la rugosité de la surface et elle influence directement l’écoulement. La sous-couche laminaire devient si mince que la rugosité de surface fait saillie dans l’écoulement. Les pertes par frottement dans ce cas sont produites dans le flux principal principalement par les éléments de rugosité saillants, et la contribution de la sous-couche laminaire est négligeable.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci
