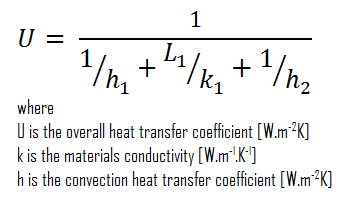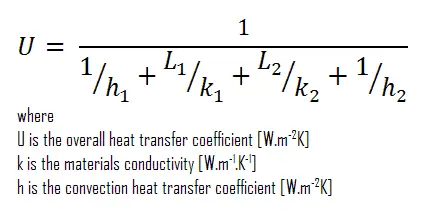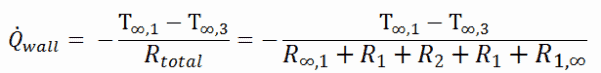Polystyrène expansé – EPS
En général, le polystyrène est un polymère aromatique synthétique fabriqué à partir du monomère styrène, dérivé du benzène et de l’éthylène, produits pétroliers. Le polystyrène peut être solide ou moussé. Le polystyrène est un thermoplastique transparent et incolore, couramment utilisé pour la fabrication d’isolants en mousse ou en aggloméré, et un type d’isolant en vrac constitué de petites billes de polystyrène. Les mousses de polystyrène contiennent de 95 à 98% d’air. Les mousses de polystyrène sont de bons isolants thermiques et sont donc souvent utilisées comme isolants de bâtiment, par exemple dans les coffrages isolants en béton et les systèmes de construction en panneaux isolés structurels. Polystyrène expansé (EPS) et extrudé (XPS)sont tous deux fabriqués à partir de polystyrène, mais l’EPS est composé de petites billes de plastique qui sont fusionnées et le XPS commence sous la forme d’un matériau fondu pressé sous forme de feuilles. Le XPS est le plus souvent utilisé comme isolant en mousse.
Le polystyrène expansé (EPS) est une mousse rigide et résistante à cellules fermées. Les applications du bâtiment et de la construction représentent environ les deux tiers de la demande de polystyrène expansé. Il est utilisé pour l’isolation des murs (creux), des toits et des sols en béton. En raison de ses propriétés techniques telles que son faible poids, sa rigidité et sa facilité de formage, le polystyrène expansé peut être utilisé dans une large gamme d’applications, par exemple des plateaux, des assiettes et des boîtes à poisson.
Bien que le polystyrène expansé et extrudé ait une structure à cellules fermées, il est perméable aux molécules d’eau et ne peut être considéré comme une barrière de vapeur. Dans le polystyrène expansé, il existe des espaces interstitiels entre les pellets expansés à cellules fermées qui forment un réseau ouvert de canaux entre les pellets liés. Si l’eau gèle dans la glace, elle se dilate et peut provoquer la rupture des pellets de polystyrène de la mousse.
Conductivité thermique du polystyrène expansé
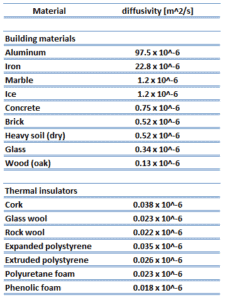 La conductivité thermique est définie comme la quantité de chaleur (en watts) transférée à travers une zone carrée de matériau d’épaisseur donnée (en mètres) en raison d’une différence de température . Plus la conductivité thermique du matériau est faible, plus la capacité du matériau à résister au transfert de chaleur est grande, et donc plus l’efficacité de l’isolation est grande. Les valeurs de conductivité thermique typique de polystyrène expansé sont comprises entre 0,030 et 0.040W / m ∙ K .
La conductivité thermique est définie comme la quantité de chaleur (en watts) transférée à travers une zone carrée de matériau d’épaisseur donnée (en mètres) en raison d’une différence de température . Plus la conductivité thermique du matériau est faible, plus la capacité du matériau à résister au transfert de chaleur est grande, et donc plus l’efficacité de l’isolation est grande. Les valeurs de conductivité thermique typique de polystyrène expansé sont comprises entre 0,030 et 0.040W / m ∙ K .
En général, l’ isolation thermique repose principalement sur la très faible conductivité thermique des gaz . Les gaz possèdent de mauvaises propriétés de conduction thermique par rapport aux liquides et aux solides et constituent donc un bon matériau d’isolation s’ils peuvent être piégés (par exemple dans une structure semblable à de la mousse). L’air et les autres gaz sont généralement de bons isolants. Mais le principal avantage est en l’absence de convection. Par conséquent, de nombreux matériaux isolants (par exemple le polystyrène expansé ) fonctionnent simplement en ayant un grand nombre de poches remplies de gaz qui empêchent la convection à grande échelle .
L’alternance de la poche de gaz et du matériau solide fait que la chaleur doit être transférée à travers de nombreuses interfaces provoquant une diminution rapide du coefficient de transfert de chaleur.
Exemple – Isolant en polystyrène expansé
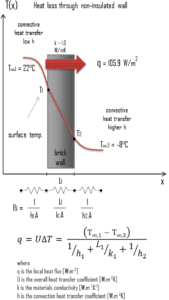 Les murs constituent une source majeure de perte de chaleur dans une maison. Calculez le taux de flux de chaleur à travers un mur de 3 mx 10 m (A = 30 m 2 ). Le mur a une épaisseur de 15 cm (L 1 ) et il est fait de briques avec une conductivité thermique de k 1 = 1,0 W / mK (mauvais isolant thermique). Supposons que les températures intérieure et extérieure sont de 22 ° C et -8 ° C et que les coefficients de transfert de chaleur par convection sur les côtés intérieur et extérieur sont h 1 = 10 W / m 2 K et h 2 = 30 W / m 2K, respectivement. A noter que ces coefficients de convection dépendent fortement notamment des conditions ambiantes et intérieures (vent, humidité, etc.).
Les murs constituent une source majeure de perte de chaleur dans une maison. Calculez le taux de flux de chaleur à travers un mur de 3 mx 10 m (A = 30 m 2 ). Le mur a une épaisseur de 15 cm (L 1 ) et il est fait de briques avec une conductivité thermique de k 1 = 1,0 W / mK (mauvais isolant thermique). Supposons que les températures intérieure et extérieure sont de 22 ° C et -8 ° C et que les coefficients de transfert de chaleur par convection sur les côtés intérieur et extérieur sont h 1 = 10 W / m 2 K et h 2 = 30 W / m 2K, respectivement. A noter que ces coefficients de convection dépendent fortement notamment des conditions ambiantes et intérieures (vent, humidité, etc.).
- Calculez le flux de chaleur ( perte de chaleur ) à travers ce mur non isolé.
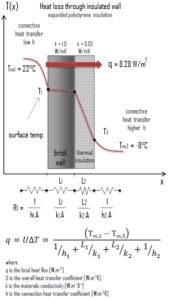
- Supposons maintenant une isolation thermique sur le côté extérieur de ce mur. Utilisez une isolation en polystyrène expansé de 10 cm d’épaisseur (L 2 ) avec une conductivité thermique de k 2 = 0,03 W / mK et calculez le flux de chaleur ( perte de chaleur ) à travers cette paroi composite.
Solution:
Comme cela a été écrit, de nombreux processus de transfert de chaleur impliquent des systèmes composites et impliquent même une combinaison de conduction et de convection . Avec ces systèmes composites, il est souvent commode de travailler avec un coefficient global de transfert de chaleur , connu comme un facteur U . Le facteur U est défini par une expression analogue à la loi de Newton du refroidissement :
Le coefficient global de transfert de chaleur est lié à la résistance thermique totale et dépend de la géométrie du problème.
- mur nu
En supposant un transfert de chaleur unidimensionnel à travers la paroi plane et sans tenir compte du rayonnement, le coefficient de transfert de chaleur global peut être calculé comme suit:
Le coefficient global de transfert de chaleur est alors:
U = 1 / (1/10 + 0,15 / 1 + 1/30) = 3,53 W / m 2 K
Le flux de chaleur peut alors être calculé simplement comme:
q = 3,53 [W / m 2 K] x 30 [K] = 105,9 W / m 2
La perte de chaleur totale à travers ce mur sera:
q perte = q. A = 105,9 [W / m 2 ] x 30 [m 2 ] = 3177 W
- mur composite avec isolation thermique
En supposant un transfert de chaleur unidimensionnel à travers la paroi composite plane, aucune résistance de contact thermique et sans tenir compte du rayonnement, le coefficient de transfert de chaleur global peut être calculé comme suit:
 Le coefficient global de transfert de chaleur est alors:
Le coefficient global de transfert de chaleur est alors:
U = 1 / (1/10 + 0,15 / 1 + 0,1 / 0,03 + 1/30) = 0,276 W / m 2 K
Le flux de chaleur peut alors être calculé simplement comme:
q = 0,276 [W / m 2 K] x 30 [K] = 8,28 W / m 2
La perte de chaleur totale à travers ce mur sera:
q perte = q. A = 8,28 [W / m 2 ] x 30 [m 2 ] = 248 W
Comme on peut le voir, un ajout d’isolant thermique entraîne une diminution importante des pertes de chaleur. Il faut l’ajouter, un ajout de la prochaine couche d’isolant thermique ne provoque pas de telles économies. Cela peut être mieux vu de la méthode de résistance thermique, qui peut être utilisée pour calculer le transfert de chaleur à travers les murs composites . Le taux de transfert thermique constant entre deux surfaces est égal à la différence de température divisée par la résistance thermique totale entre ces deux surfaces.
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci