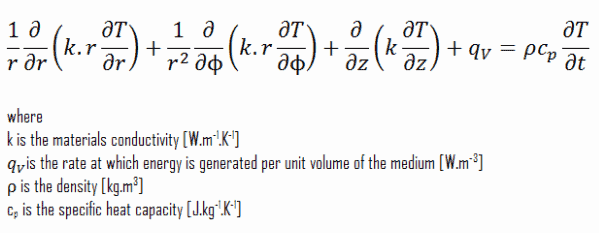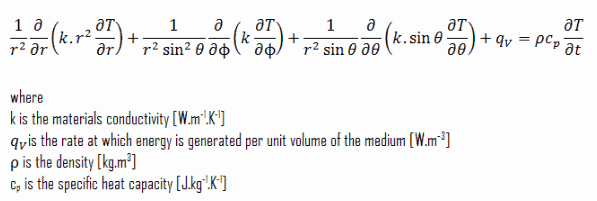Equation de chaleur en coordonnées cylindriques et sphériques
En ingénierie, il y a beaucoup de problèmes, qui ne peuvent pas être résolus en coordonnées cartésiennes. Les systèmes cylindriques et sphériques sont très courants en thermique et en particulier en génie électrique. L’équation de la chaleur peut également être exprimée en coordonnées cylindriques et sphériques. L’ équation générale de la conduction thermique en coordonnées cylindriques peut être obtenue à partir d’un bilan énergétique d’un élément de volume en coordonnées cylindriques et à l’aide de l’ opérateur de Laplace, Δ, sous forme cylindrique et sphérique .
Coordonnées cylindriques:
Coordonnées sphériques:
Obtenir des solutions analytiques à ces équations différentielles nécessite une connaissance des techniques de résolution des équations différentielles partielles, ce qui dépasse le cadre de ce texte. Par ailleurs, de nombreuses simplifications et hypothèses pouvant être appliquées à ces équations donnent lieu à des résultats très importants. Dans la section suivante, nous limiterons notre examen aux cas unidimensionnels à l’état stable à conductivité thermique constante, car ils conduisent à des équations différentielles ordinaires.