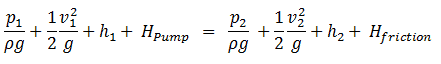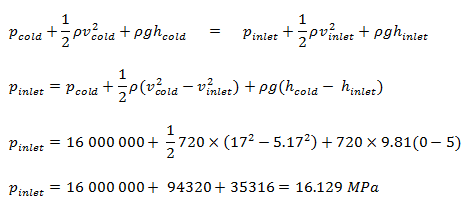O que é a equação de Bernoulli – Princípio de Bernoulli – Definição

Conservação de energia

Esse princípio é geralmente conhecido como o princípio de conservação de energia e afirma que a energia total de um sistema isolado permanece constante – diz-se que é conservada ao longo do tempo. Isso é equivalente à Primeira Lei da Termodinâmica , que é usada para desenvolver a equação geral de energia na termodinâmica. Este princípio pode ser usado na análise de fluxo de fluidos e este princípio é expressa matematicamente pela seguinte equação: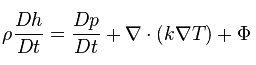onde h é entalpia, k é a condutividade térmica do fluido, T é a temperatura e Φ é a função de dissipação viscosa.

Equação de Bernoulli

A equação de Bernoulli pode ser considerada uma afirmação do princípio de conservação de energia apropriado para fluidos fluidos. É uma das equações mais importantes / úteis na mecânica de fluidos . Ele coloca em uma relação pressão e velocidade em um fluxo incompreensível inviscível . A equação de Bernoulli tem algumas restrições em sua aplicabilidade, resumidas nos seguintes pontos:

• sistema de fluxo constante,
• a densidade é constante (o que também significa que o fluido é incompressível),
• nenhum trabalho é feito sobre ou pelo fluido,
• nenhum calor é transferido para ou a partir do fluido,
• nenhuma mudança ocorre na energia interna,
• a equação relaciona os estados em dois pontos ao longo de uma única linha de fluxo (não condições em duas linhas de fluxo diferentes)

Sob essas condições, a equação geral de energia é simplificada para:

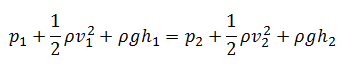
Esta equação é a equação mais famosa na dinâmica de fluidos . A equação de Bernoulli descreve o comportamento qualitativo que flui fluido que geralmente é rotulado com o termo efeito de Bernoulli . Esse efeito causa a redução da pressão do fluido em regiões onde a velocidade do fluxo é aumentada. Esse abaixamento da pressão em uma constrição de um caminho de fluxo pode parecer contra-intuitivo, mas parece menos quando você considera a pressão como densidade de energia. No fluxo de alta velocidade através da constrição, a energia cinética deve aumentar à custa da energia de pressão. As dimensões dos termos na equação são energia cinética por unidade de volume.

Equação de Bernoulli estendida

Existem duas premissas principais que foram aplicadas na derivação da equação de Bernoulli simplificada .

• A primeira restrição à equação de Bernoulli é que nenhum trabalho pode ser realizado no fluido ou por ele. Essa é uma limitação significativa, porque a maioria dos sistemas hidráulicos (especialmente em engenharia nuclear ) inclui bombas. Essa restrição impede que dois pontos em uma corrente de fluido sejam analisados ​​se existir uma bomba entre os dois pontos.

• A segunda restrição à equação simplificada de Bernoulli é que nenhum atrito de fluido é permitido na solução de problemas hidráulicos. Na realidade, o atrito desempenha papel crucial . A cabeça total possuída pelo fluido não pode ser transferida completamente e sem perdas de um ponto para outro. Na realidade, um objetivo das bombas incorporadas em um sistema hidráulico é superar as perdas de pressão devido ao atrito.

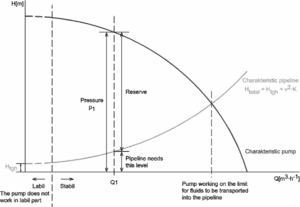
Devido a essas restrições, a maioria das aplicações práticas da equação de Bernoulli simplificada para sistemas hidráulicos reais é muito limitada. Para lidar com as perdas de carga e o trabalho da bomba, a equação de Bernoulli simplificada deve ser modificada .

A equação de Bernoulli pode ser modificada para levar em conta ganhos e perdas de cabeça . A equação resultante, referida como a equação de Bernoulli estendida , é muito útil na solução da maioria dos problemas de fluxo de fluidos. A equação a seguir é uma forma da equação de Bernoulli estendida.

em que:
h = altura acima do nível de referência (m)
v = velocidade média do fluido (m / s)
p = pressão do fluido (Pa)
H _bomba = cabeçote adicionado pela bomba (m)
H _atrito = perda de cabeçote devido ao atrito do fluido ( m)
g = aceleração devido à gravidade (m / s ² )

A perda de carga (ou a perda de pressão) devido à fricção de fluido (H _atrito ) representa a energia utilizada para vencer o atrito causado por as paredes do tubo. A perda de carga que ocorre nos tubos é dependente da velocidade do fluxo, diâmetro e comprimento do tubo , e um fator de atrito baseado na rugosidade do tubo e no número de Reynolds do fluxo. Um sistema de tubulação contendo muitos encaixes e juntas de tubos, convergência de tubos, divergência, espiras, rugosidade da superfície e outras propriedades físicas também aumentará a perda de carga de um sistema hidráulico.

Embora a perda de carga represente uma perda de energia , ela não representa uma perda de energia total do fluido. A energia total do fluido conserva como conseqüência da lei de conservação de energia . Na realidade, a perda de carga devido ao atrito resulta em um aumento equivalente na energia interna (aumento da temperatura) do fluido.

A maioria dos métodos para avaliar a perda de carga por atrito é baseada quase que exclusivamente em evidências experimentais. Isso será discutido nas próximas seções.

Exemplos – Princípio de Bernoulli

Efeito de Bernoulli – Relação entre pressão e velocidade

É um exemplo ilustrativo, os dados a seguir não correspondem a nenhum projeto de reator.

Quando a equação de Bernoulli é combinada com a equação de continuidade, as duas podem ser usadas para encontrar velocidades e pressões em pontos do fluxo conectados por uma linha de corrente.

A equação de continuidade é simplesmente uma expressão matemática do princípio de conservação de massa . Para um volume de controle que possui uma única entrada e uma única saída , o princípio de conservação de massa afirma que, para o fluxo em estado estacionário , a taxa de fluxo de massa no volume deve ser igual à taxa de fluxo de massa.

Exemplo:

Determine a pressão e a velocidade dentro de uma perna fria da tubulação primária e determine a pressão e a velocidade no fundo de um núcleo do reator , que fica cerca de 5 metros abaixo da perna fria da tubulação primária.

Vamos assumir:

• Fluido de densidade constante ⍴ ~ 720 kg / m ³ (a 290 ° C) está fluindo continuamente através da perna fria e através da parte inferior do núcleo.

• A seção transversal do fluxo da tubulação primária (loop único) é igual a 0,385 m ² (diâmetro da tubulação ~ 700 mm)

• A velocidade do fluxo na perna fria é igual a 17 m / s .

• A seção transversal do fluxo do núcleo do reator é igual a 5m ² .

• A pressão manométrica dentro da perna fria é igual a 16 MPa .

Como resultado do princípio da continuidade, a velocidade na parte inferior do núcleo é:

v _entrada = v _frio . Uma _tubulação / _núcleo A = 17 x 1,52 / 5 = 5,17 m / s

Como resultado do princípio de Bernoulli, a pressão na parte inferior do núcleo (entrada do núcleo) é:

Princípio de Bernoulli – Força de Elevação

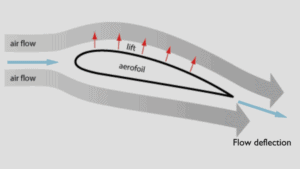
Em geral, o elevador é uma força de ação ascendente na asa da aeronave ou aerofólio . Existem várias maneiras de explicar como um aerofólio gera sustentação . Algumas teorias são mais complicadas ou matematicamente rigorosas do que outras. Algumas teorias demonstraram estar incorretas. Existem teorias baseadas no princípio de Bernoulli e há teorias baseadas diretamente na terceira lei de Newton .

A explicação baseada na terceira lei de Newton afirma que o levantamento é causado por uma deflexão do fluxo da corrente de ar atrás do aerofólio. O aerofólio gera sustentação ao exercer uma força descendente no ar à medida que passa. De acordo com a terceira lei de Newton, o ar deve exercer uma força ascendente no aerofólio . Esta é uma explicação muito simples.

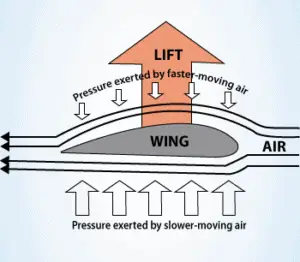
O princípio de Bernoulli combinado com a equação de continuidade também pode ser usado para determinar a força de sustentação em um aerofólio, se o comportamento do fluxo de fluido na vizinhança da película for conhecido. Nesta explicação, a forma de um aerofólio é crucial. A forma de um aerofólio faz com que o ar flua mais rapidamente por cima e por baixo. De acordo com o princípio de Bernoulli , o ar em movimento mais rápido exerce menos pressão e, portanto, o ar deve exercer uma força ascendente no aerofólio (como resultado de uma diferença de pressão).

O princípio de Bernoulli exige que o aerofólio tenha uma forma assimétrica . Sua área de superfície deve ser maior na parte superior do que na parte inferior. À medida que o ar flui sobre o aerofólio, ele é deslocado mais pela superfície superior do que por baixo. De acordo com o princípio da continuidade , esse deslocamento deve levar a um aumento na velocidade do fluxo (resultando em uma diminuição na pressão). A velocidade do fluxo é aumentada um pouco pela superfície inferior do aerofólio, mas consideravelmente menor do que o fluxo na superfície superior. A força de sustentação de um aerofólio, caracterizada pelo coeficiente de sustentação , pode ser alterada durante o vôo por alterações na forma de um aerofólio. O coeficiente de elevação pode, portanto, ser duplicado com dispositivos relativamente simples (flaps e slats ) se usado em toda a extensão da asa.O uso do princípio de Bernoulli pode não estar correto. O princípio de Bernoulli pressupõe incompressibilidade do ar, mas, na realidade, o ar é facilmente compressível. Mas existem mais limitações de explicações baseadas no princípio de Bernoulli. Existem duas explicações populares principais sobre o elevador:

• Explicação baseada na deflexão descendente do fluxo – terceira lei de Newton
• Explicação baseada em mudanças na velocidade e pressão do fluxo – Princípio da continuidade e princípio de Bernoulli

Ambas as explicações identificam corretamente alguns aspectos das forças de sustentação, mas deixam outros aspectos importantes do fenômeno inexplicáveis. Uma explicação mais abrangente envolve mudanças na velocidade do fluxo e deflexão para baixo e requer uma análise mais detalhada do fluxo.

Veja mais: Doug McLean, Entendendo a aerodinâmica: discutindo a partir da física real. John Wiley & Sons Ltd. 2013. ISBN: 978-1119967514

Efeito de Bernoulli – Girando a bola no fluxo de ar

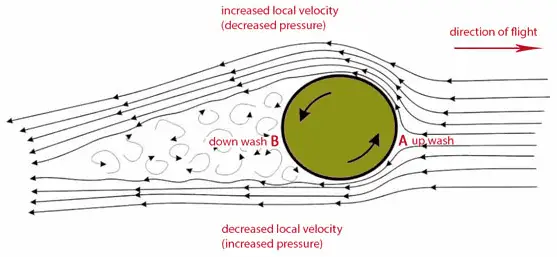O efeito de Bernoulli tem outra conseqüência interessante interessante. Suponha que uma bola esteja girando enquanto viaja pelo ar. À medida que a bola gira, o atrito da superfície da bola com o ar circundante arrasta uma camada fina (denominada camada limite ) de ar. Pode ser visto na figura que a camada limite está de um lado viajando na mesma direção que a corrente de ar que flui ao redor da bola (seta superior) e, por outro lado, a camada limite está viajando na direção oposta ( a seta inferior). No lado da bola, onde a corrente de ar e a camada limite estão se movendo na direção oposta (a seta inferior) entre si, o atrito entre as duasretarda a corrente de ar . No lado oposto, essas camadas estão se movendo na mesma direção e o fluxo se move mais rápido .

De acordo com o princípio de Bernoulli , o ar em movimento mais rápido exerce menos pressão e, portanto, o ar deve exercer uma força ascendente na bola. De fato, neste caso, o uso do princípio de Bernoulli pode não estar correto. O princípio de Bernoulli assume incompressibilidade do ar, mas, na realidade, o ar é facilmente compressível. Mas existem mais limitações de explicações baseadas no princípio de Bernoulli.

O trabalho de Robert G. Watts e Ricardo Ferrer (as forças laterais em uma esfera giratória: aerodinâmica de uma bola curva) esse efeito pode ser explicado por outro modelo que dá uma atenção importante à camada limite de ar em torno da bola. No lado da bola onde a corrente de ar e a camada limite se movem na direção oposta (seta inferior), a camada limite tende a se separar prematuramente. No lado da bola onde o fluxo de ar e a camada limite se movem na mesma direção, a camada limite carrega ainda mais a bola antes de se separar em fluxo turbulento. Isso dá uma deflexão do fluxoda corrente de ar em uma direção atrás da bola. A bola em rotação gera sustentação, exercendo uma força descendente no ar à medida que flui. De acordo com a terceira lei de Newton , o ar deve exercer uma força ascendente na bola.

Lei de Torricelli

A lei de Torricelli , também conhecida como princípio de Torricelli , ou teorema de Torricelli , afirma na dinâmica dos fluidos que a velocidade, v, do fluido que sai de um orifício sob a força da gravidade em um tanque é proporcional à raiz quadrada da distância vertical, h , entre a superfície do líquido e o centro do orifício e a raiz quadrada de duas vezes a aceleração causada pela gravidade (g = 9,81 N / kg perto da superfície da Terra).

Em outras palavras, a velocidade de efluxo do fluido do orifício é a mesma que teria adquirido ao cair uma altura h abaixo da gravidade. A lei foi descoberta e nomeada em homenagem ao cientista italiano Evangelista Torricelli , em 1643. Mais tarde, mostrou-se um caso particular do princípio de Bernoulli .

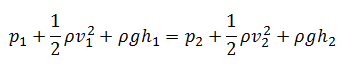
A equação de Torricelli é derivada para uma condição específica. O orifício deve ser pequeno e a viscosidade e outras perdas devem ser ignoradas. Se um fluido está fluindo através de um orifício muito pequeno (por exemplo, no fundo de um tanque grande), a velocidade do fluido na extremidade maior pode ser negligenciada na Equação de Bernoulli. Além disso, a velocidade do efluxo é independente da direção do fluxo. Nesse caso, a velocidade de efluxo do fluido que flui através do orifício dada pela seguinte fórmula:

v = √ 2gh