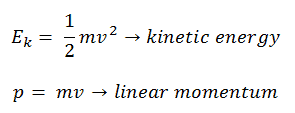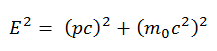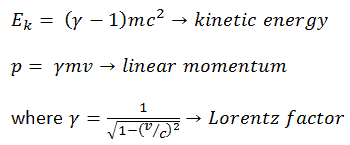Energia cinética relativística
A relação anterior entre trabalho e energia cinética é baseada nas leis do movimento de Newton . Quando generalizamos essas leis de acordo com o princípio da relatividade, precisamos de uma generalização correspondente da equação para a energia cinética . Se a velocidade de um objeto é próxima da velocidade da luz, é necessário usar a mecânica relativística para calcular sua energia cinética .
Na mecânica clássica , energia cinética e momento são expressos como:
A derivação de suas relações relativísticas é baseada na relação energia-momento relativista :
Pode-se derivar, a energia cinética relativística e o momento relativístico são:
O primeiro termo ( ɣmc 2 ) da energia cinética relativística aumenta com a velocidade v da partícula. O segundo termo ( mc 2 ) é constante; é chamada de energia restante (massa restante) da partícula e representa uma forma de energia que uma partícula possui mesmo quando em velocidade zero . À medida que a velocidade de um objeto se aproxima da velocidade da luz, a energia cinética se aproxima do infinito . É causada pelo fator de Lorentz , que se aproxima do infinito para v → c . Portanto, a velocidade da luz não pode ser alcançada por partículas maciças.
O primeiro termo (ɣmc 2 ) é conhecido como energia total E da partícula, porque é igual à energia restante mais a energia cinética:
E = K + mc 2
Para uma partícula em repouso, ou seja, K é zero, então a energia total é sua energia de repouso:
E = mc 2
Este é um dos resultados marcantes da teoria da relatividade de Einstein é que massa e energia são equivalentes e conversíveis um no outro. A equivalência entre massa e energia é descrita pela famosa fórmula de Einstein E = mc 2 . Este resultado foi confirmado experimentalmente inúmeras vezes na física de partículas nuclear e elementar. Por exemplo, consulte Produção de pares de pósitrons com elétrons ou conservação de energia em reações nucleares .
Veja também: Massa relativística
Exemplo: energia cinética do próton
Um próton ( m = 1,67 x 10-27 kg ) viaja a uma velocidade v = 0,9900c = 2,968 x 10 8 m / s . Qual é a sua energia cinética ?
De acordo com um cálculo clássico, que não está correto, obteríamos:
K = 1 / 2mv 2 = ½ x (1,67 x 10-27 kg) x (2,968 x 10 8 m / s) 2 = 7,355 x 10 -11 J
Com a correção relativística, a energia cinética relativística é igual a:
K = (ɣ – 1) mc 2
onde o fator de Lorentz
ɣ = 7.089
Portanto
K = 6,089 x (1,67 x 10 -27 kg) x (2,9979 x 10 8 m / s) 2 = 9,139 x 10-10 J = 5,701 GeV
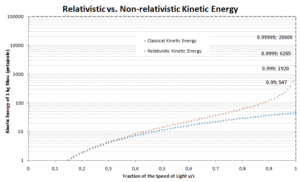
Isso é cerca de 12 vezes mais energia do que no cálculo clássico. De acordo com essa relação, a aceleração de um feixe de prótons para 5,7 GeV requer energias da ordem diferente.
……………………………………………………………………………………………………………………………….
Este artigo é baseado na tradução automática do artigo original em inglês. Para mais informações, consulte o artigo em inglês. Você pode nos ajudar. Se você deseja corrigir a tradução, envie-a para: translations@nuclear-power.com ou preencha o formulário de tradução on-line. Agradecemos sua ajuda, atualizaremos a tradução o mais rápido possível. Obrigado.
