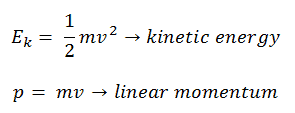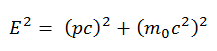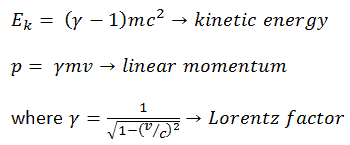Energía cinética relativista
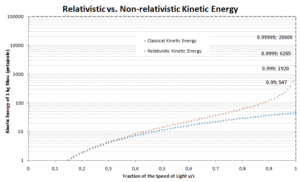
La relación previa entre el trabajo y la energía cinética se basa en las leyes del movimiento de Newton . Cuando generalizamos estas leyes de acuerdo con el principio de relatividad, necesitamos una generalización correspondiente de la ecuación para la energía cinética . Si la velocidad de un objeto está cerca de la velocidad de la luz, es necesario utilizar una mecánica relativista para calcular su energía cinética .
En mecánica clásica , la energía cinética y el momento se expresan como:
La derivación de sus relaciones relativistas se basa en la relación relativista energía-momento:
Se puede derivar, la energía cinética relativista y el momento relativista son:
El primer término ( ɣmc 2 ) de la energía cinética relativista aumenta con la velocidad v de la partícula. El segundo término ( mc 2 ) es constante; Se llama energía en reposo (masa en reposo) de la partícula y representa una forma de energía que tiene una partícula incluso cuando está a velocidad cero . Cuando la velocidad de un objeto se acerca a la velocidad de la luz, la energía cinética se acerca al infinito . Es causada por el factor Lorentz , que se acerca al infinito para v → c . Por lo tanto, la velocidad de la luz no puede ser alcanzada por ninguna partícula masiva.
El primer término (ɣmc 2 ) se conoce como la energía total E de la partícula, porque es igual a la energía en reposo más la energía cinética:
E = K + mc 2
Para una partícula en reposo, es decir, K es cero, por lo que la energía total es su energía en reposo:
E = mc 2
Este es uno de los resultados sorprendentes de la teoría de la relatividad de Einstein es que la masa y la energía son equivalentes y convertibles una en la otra. La famosa fórmula E = mc 2 describe la equivalencia de la masa y la energía . Este resultado ha sido confirmado experimentalmente innumerables veces en física de partículas nucleares y elementales. Por ejemplo, vea Producción de pares de positrones-electrones o Conservación de energía en reacciones nucleares .
Ver también: masa relativista
Ejemplo: energía cinética de protón
Un protón ( m = 1.67 x 10 -27 kg ) viaja a una velocidad v = 0.9900c = 2.968 x 10 8 m / s . ¿Cuál es su energía cinética ?
Según un cálculo clásico, que no es correcto, obtendríamos:
K = 1 / 2mV 2 = ½ x (1,67 x 10 -27 kg) x (2.968 x 10 8 m / s) 2 = 7,355 x 10 -11 J
Con la corrección relativista, la energía cinética relativista es igual a:
K = (ɣ – 1) mc 2
donde el factor de Lorentz
ɣ = 7.089
por lo tanto
K = 6.089 x (1.67 x 10 -27 kg) x (2.9979 x 10 8 m / s) 2 = 9.139 x 10-10 J = 5.701 GeV
Esto es aproximadamente 12 veces más energía que en el cálculo clásico. De acuerdo con esta relación, una aceleración de un haz de protones a 5.7 GeV requiere energías que son diferentes en el orden.
……………………………………………………………………………………………………………………………….
Este artículo se basa en la traducción automática del artículo original en inglés. Para más información vea el artículo en inglés. Puedes ayudarnos. Si desea corregir la traducción, envíela a: translations@nuclear-power.com o complete el formulario de traducción en línea. Agradecemos su ayuda, actualizaremos la traducción lo antes posible. Gracias.
