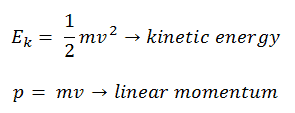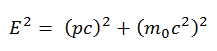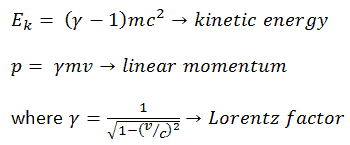Facebook Instagram Youtube Twitter

What is Relativistic Kinetic Energy – Definition

by
As velocity of an object approaches the speed of light, the relativistic kinetic energy approaches infinity. Relativistic kinetic energy formula is based on the relativistic energy-momentum relation. Thermal Engineering

Relativistic Kinetic Energy

relativistic kinetic energy
As velocity of an object approaches the speed of light, the relativistic kinetic energy approaches infinity. It is caused by the Lorentz factor, which approaches infinity for v → c.

The previous relationship between work and kinetic energy are based on Newton’s laws of motion. When we generalize these laws according to the principle of relativity, we need a corresponding generalization of the equation for kinetic energy. If an object’s speed is close to the speed of light, it is necessary to use relativistic mechanics to calculate its kinetic energy.

In classical mechanics, kinetic energy and momentum are expressed as:

classical momentum and kinetic energy

Derivation of its relativistic relationships is based on the relativistic energy-momentum relation:

energy-momentum relation

It can be derived, the relativistic kinetic energy and the relativistic momentum are:

relativistic kinetic energy - formula

The first term (ɣmc2) of the relativistic kinetic energy increases with the speed v of the particle. The second term (mc2) is constant; it is called the rest energy (rest mass) of the particle, and represents a form of energy that a particle has even when at zero velocity. As velocity of an object approaches the speed of light, the kinetic energy approaches infinity. It is caused by the Lorentz factor, which approaches infinity for v → c. Therefore the speed of light cannot be reached by any massive particles.

The first term (ɣmc2) is known as the total energy E of the particle, because it equals the rest energy plus the kinetic energy:

E = K + mc2

For a particle at rest, i.e. K is zero, so the total energy is its rest energy:

E = mc2

This is one of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible one into the other. Equivalence of the mass and energy is described by Einstein’s famous formula E = mc2. This result have been experimentally confirmed countless times in nuclear and elementary particle physics. For example, see Positron-electron Pair Production or Conservation of Energy in Nuclear Reactions.

See also: Relativistic Mass

Example: Proton’s kinetic energy

What is proton - physicsA proton (m = 1.67 x 10-27 kg) travels at a speed v = 0.9900c = 2.968 x 108m/s. What is its kinetic energy?

According to a classical calculation, which is not correct, we would obtain:

K = 1/2mv2 = ½ x (1.67 x 10-27 kg) x (2.968 x 108m/s)2 = 7.355 x 10-11 J

With relativistic correction the relativistic kinetic energy is equal to:

K = (ɣ – 1)mc2

where the Lorentz factor

ɣ = 7.089

therefore

K = 6.089 x (1.67 x 10-27 kg) x (2.9979 x 108m/s)2 = 9.139 x 10-10 J = 5.701 GeV

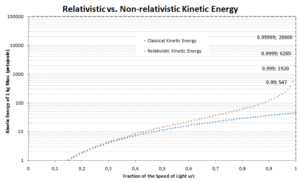
This is about 12 times higher energy as in the classical calculation. According to this relationship, an acceleration of a proton beam to 5.7 GeV requires energies that are in the order different.

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2 and 3. June 1992.

See also:

Kinetic Energy

We hope, this article, Relativistic Kinetic Energy, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts