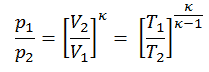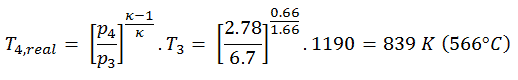Facebook Instagram Youtube Twitter

What is Adiabatic Expansion – Adiabatic Compression – Definition

2019-06-032019-05-22 by Nick Connor

Adiabatic Expansion – Adiabatic Compression. Adiabatic compression and expansion are processes very important in thermal analysis of thermal power plants. Thermal Engineering

Adiabatic Process

An adiabatic process is a thermodynamic process, in which there is no heat transfer into or out of the system (Q = 0). The system can be considered to be perfectly insulated. In an adiabatic process, energy is transferred only as work. The assumption of no heat transfer is very important, since we can use the adiabatic approximation only in very rapid processes. In these rapid processes, there is not enough time for the transfer of energy as heat to take place to or from the system.

In real devices (such as turbines, pumps, and compressors) heat losses and losses in the combustion process occur, but these losses are usually low in comparison to overall energy flow and we can approximate some thermodynamic processes by the adiabatic process.

Main characteristics of adiabatic process

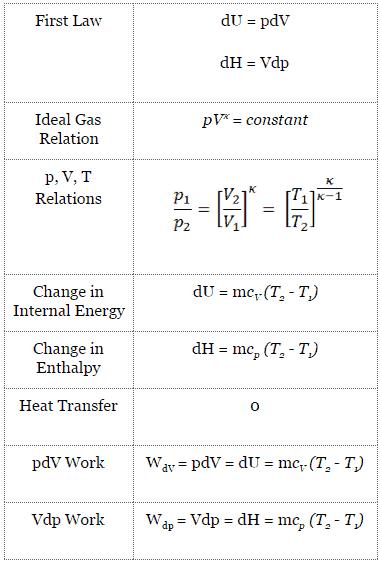
See also: First Law of Thermodynamics

See also: Ideal Gas Law

See also: What is Enthalpy

Adiabatic Expansion – Adiabatic Compression

See also: What is an Ideal Gas

In an ideal gas, molecules have no volume and do not interact. According to the ideal gas law, pressure varies linearly with temperature and quantity, and inversely with volume.

pV = nRT

where:

p is the absolute pressure of the gas
n is the amount of substance
T is the absolute temperature
V is the volume
R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,

In this equation the symbol R is a constant called the universal gas constant that has the same value for all gases—namely, R = 8.31 J/mol K.

The adiabatic process can be expressed with the ideal gas law as:

pV^κ = constant

or

p₁V₁^κ = p₂V₂^κ

in which κ = c_p/c_v is the ratio of the specific heats (or heat capacities) for the gas. One for constant pressure (c_p) and one for constant volume (c_v). Note that, this ratio κ = c_p/c_v is a factor in determining the speed of sound in a gas and other adiabatic processes.

Other p, V, T Relation

On a p-V diagram, the process occurs along a line (called an adiabat) that has the equation p = constant / V^κ. For an ideal gas and a polytropic process, the case n = κ corresponds to an adiabatic process.

Example of Adiabatic Expansion

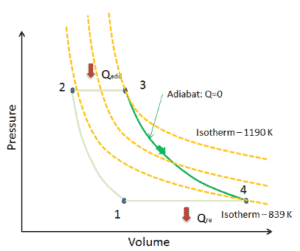
P-V diagram - adiabatic process — Assume an adiabatic expansion of helium (3 → 4) in a gas turbine (Brayton cycle).

Assume an adiabatic expansion of helium (3 → 4) in a gas turbine. Since helium behaves almost as an ideal gas, use the ideal gas law to calculate outlet temperature of the gas (T_4,real). In this turbines the high-pressure stage receives gas (point 3 at the figure; p₃= 6.7 MPa; T₃ = 1190 K (917°C)) from a heat exchanger and exhaust it to another heat exchanger, where the outlet pressure is p₄ = 2.78 MPa (point 4).

Solution:

The outlet temperature of the gas, T_4,real, can be calculated using p, V, T Relation for adiabatic process. Note that, it is the same relation as for the isentropic process, therefore results must be identical. It this case, we calculate the expansion for different gas turbine (less efficient) as in case of Isentropic Expansion in Gas Turbine.

In this equation the factor for helium is equal to κ=c_p/c_v=1.66. From the previous equation follows that the outlet temperature of the gas, T_4,real, is:

See also: Mayer’s relation

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Adiabatic Process

We hope, this article, Adiabatic Expansion – Adiabatic Compression, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.