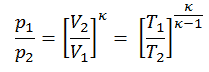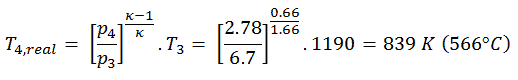Processus adiabatique
Un processus adiabatique est un processus thermodynamique dans lequel il n’y a pas de transfert de chaleur dans ou hors du système (Q = 0). Le système peut être considéré comme parfaitement isolé . Dans un processus adiabatique, l’énergie n’est transférée qu’en tant que travail. L’hypothèse d’absence de transfert de chaleur est très importante, car l’approximation adiabatique ne peut être utilisée que dans des processus très rapides . Dans ces processus rapides, le transfert d’énergie sous forme de chaleur vers ou depuis le système est insuffisant.
Dans les appareils réels (comme les turbines, les pompes et les compresseurs), des pertes de chaleur et des pertes dans le processus de combustion se produisent, mais ces pertes sont généralement faibles par rapport au flux énergétique global et nous pouvons approcher certains processus thermodynamiques par le processus adiabatique.
Voir aussi: Première loi de la thermodynamique
Voir aussi: Loi sur les gaz parfaits
Voir aussi: Qu’est-ce que l’enthalpie?
Expansion adiabatique – Compression adiabatique
Voir aussi: Qu’est-ce qu’un gaz parfait?
Dans un gaz parfait , les molécules n’ont pas de volume et n’interagissent pas. Selon la loi des gaz parfaits , la pression varie linéairement avec la température et la quantité, et inversement avec le volume .
pV = nRT
où:
- p est la pression absolue du gaz
- n est la quantité de substance
- T est la température absolue
- V est le volume
- R est la constante de gaz parfaite ou universelle, égale au produit de la constante de Boltzmann et de la constante d’Avogadro,
Dans cette équation, le symbole R est une constante appelée constante de gaz universelle qui a la même valeur pour tous les gaz, à savoir R = 8,31 J / mol K.
Le processus adiabatique peut s’exprimer avec la loi du gaz parfait comme:
pV κ = constant
ou
p 1 V 1 κ = p 2 V 2 κ
dans laquelle κ = c p / c v est le rapport des chaleurs spécifiques (ou capacités calorifiques ) pour le gaz. Un pour une pression constante (c p ) et un pour un volume constant (c v ) . Notez que ce rapport κ = c p / c v est un facteur déterminant la vitesse du son dans un gaz et d’autres processus adiabatiques.
Autre relation p, V, T
Sur un diagramme pV , le processus se produit le long d’une ligne (appelée adiabat ) qui a l’équation p = constante / V κ . Pour un gaz parfait et un processus polytropique, le cas n = κ correspond à un processus adiabatique.
Exemple d’expansion adiabatique
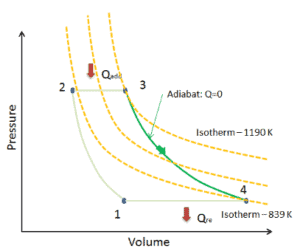
Supposons une expansion adiabatique d’hélium ( 3 → 4 ) dans une turbine à gaz . L’hélium se comportant presque comme un gaz parfait , utilisez la loi du gaz parfait pour calculer la température de sortie du gaz ( T 4, réel ). Dans ces turbines, l’étage haute pression reçoit du gaz (point 3 sur la figure; p 3 = 6,7 MPa ; T 3 = 1190 K (917 ° C)) d’un échangeur de chaleur et l’évacue vers un autre échangeur de chaleur, où la pression de sortie est p 4 = 2,78 MPa (point 4) .
Solution:
La température de sortie du gaz, T 4, réel , peut être calculée en utilisant la relation p, V, T pour le processus adiabatique. Notez que, c’est la même relation que pour le processus isentropique , donc les résultats doivent être identiques. Dans ce cas, nous calculons l’expansion pour différentes turbines à gaz (moins efficaces) comme dans le cas d’une expansion isentropique dans une turbine à gaz.
Dans cette équation, le facteur pour l’hélium est égal à κ = c p / c v = 1,66 . Il résulte de l’équation précédente que la température de sortie du gaz, T 4, réel , est:
Voir aussi: la relation de Mayer
……………………………………………………………………………………………………………………………….
Cet article est basé sur la traduction automatique de l’article original en anglais. Pour plus d’informations, voir l’article en anglais. Pouvez vous nous aider Si vous souhaitez corriger la traduction, envoyez-la à l’adresse: translations@nuclear-power.com ou remplissez le formulaire de traduction en ligne. Nous apprécions votre aide, nous mettrons à jour la traduction le plus rapidement possible. Merci