Enthalpy Formulas in Extensive Units
H = U + pV
Enthalpy is an extensive quantity, it depends on the size of the system, or on the amount of substance it contains. The SI unit of enthalpy is the joule (J). It is the energy contained within the system, excluding the kinetic energy of motion of the system as a whole and the potential energy of the system as a whole due to external force fields. It is the thermodynamic quantity equivalent to the total heat content of a system.
On the other hand, energy can be stored in the chemical bonds between the atoms that make up the molecules. This energy storage on the atomic level includes energy associated with electron orbital states, nuclear spin, and binding forces in the nucleus.
Enthalpy is represented by the symbol H, and the change in enthalpy in a process is H2 – H1.
There are enthalpy formulas in terms of more familiar variables such as temperature and pressure:
dH = CpdT + V(1-αT)dp
Where Cp is the heat capacity at constant pressure and α is the coefficient of (cubic) thermal expansion. For ideal gas αT = 1 and therefore:
dH = CpdT
Enthalpy Formulas in Intensive Units – Specific Enthalpy
The enthalpy can be made into an intensive, or specific, variable by dividing by the mass. Engineers use the specific enthalpy in thermodynamic analysis more than the enthalpy itself. The specific enthalpy (h) of a substance is its enthalpy per unit mass. It equals to the total enthalpy (H) divided by the total mass (m).
h = H/m
where:
h = specific enthalpy (J/kg)
H = enthalpy (J)
m = mass (kg)
Note that the enthalpy is the thermodynamic quantity equivalent to the total heat content of a system. The specific enthalpy is equal to the specific internal energy of the system plus the product of pressure and specific volume.
h = u + pv
In general, enthalpy is a property of a substance, like pressure, temperature, and volume, but it cannot be measured directly. Normally, the enthalpy of a substance is given with respect to some reference value. For example, the specific enthalpy of water or steam is given using the reference that the specific enthalpy of water is zero at 0.01°C and normal atmospheric pressure, where hL = 0.00 kJ/kg. The fact that the absolute value of specific enthalpy is unknown is not a problem, however, because it is the change in specific enthalpy (∆h) and not the absolute value that is important in practical problems.
Formulas for Specific Enthalpy of Wet Steam
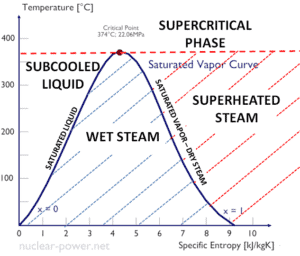 The specific enthalpy of saturated liquid water (x=0) and dry steam (x=1) can be picked from steam tables. In case of wet steam, the actual enthalpy can be calculated with the vapor quality, x, and the specific enthalpies of saturated liquid water and dry steam:
The specific enthalpy of saturated liquid water (x=0) and dry steam (x=1) can be picked from steam tables. In case of wet steam, the actual enthalpy can be calculated with the vapor quality, x, and the specific enthalpies of saturated liquid water and dry steam:
hwet = hs x + (1 – x ) hl
where
hwet = enthalpy of wet steam (J/kg)
hs = enthalpy of “dry” steam (J/kg)
hl = enthalpy of saturated liquid water (J/kg)
As can be seen, wet steam will always have lower enthalpy than dry steam.
Example:
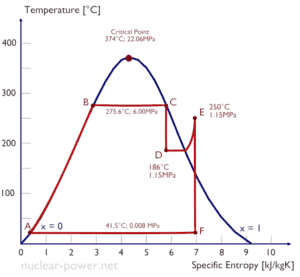
A high-pressure stage of steam turbine operates at steady state with inlet conditions of 6 MPa, t = 275.6°C, x = 1 (point C). Steam leaves this stage of turbine at a pressure of 1.15 MPa, 186°C and x = 0.87 (point D). Calculate the enthalpy difference between these two states.
The enthalpy for the state C can be picked directly from steam tables, whereas the enthalpy for the state D must be calculated using vapor quality:
h1, wet = 2785 kJ/kg
h2, wet = h2,s x + (1 – x ) h2,l = 2782 . 0.87 + (1 – 0.87) . 790 = 2420 + 103 = 2523 kJ/kg
Δh = 262 kJ/kg
We hope, this article, Enthalpy Formula – Equation, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.