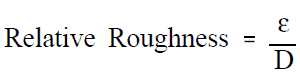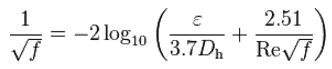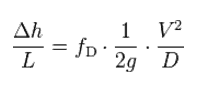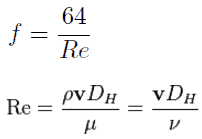Fanning Friction Factor
There are two common friction factors in use, the Darcy and the Fanning friction factors.
The Fanning friction factor, named after John Thomas Fanning, is a dimensionless number, that is one-fourth of the Darcy friction factor, so attention must be paid to note which one of these is used as the friction factor. This the only difference between these two factors. In all other aspects they are identical, and by applying the conversion factor of 4 the friction factors may be used interchangeably.
fD = 4.fF
The friction factor has been determined to depend on the Reynolds number for the flow and the degree of roughness of the pipe’s inner surface (especially for turbulent flow). The friction factor of laminar flow is independent of roughness of the pipe’s inner surface.
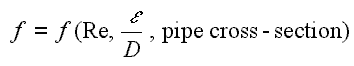
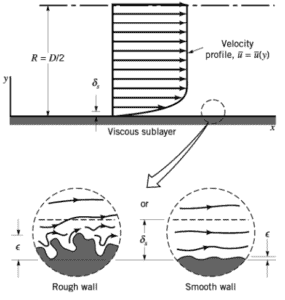
The pipe cross-section is also important, as deviations from circular cross-section will cause secondary flows that increase the head loss. Non-circular pipes and ducts are generally treated by using the hydraulic diameter.
Summary:
- Head loss of hydraulic system is divided into two main categories:
- Major Head Loss – due to friction in straight pipes
- Minor Head Loss – due to components as valves, bends…
- Darcy’s equation can be used to calculate major losses.
- The friction factor for fluid flow can be determined using a Moody chart.
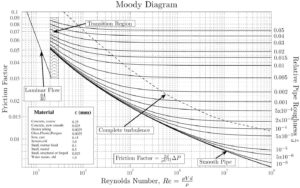
- The friction factor for laminar flow is independent of roughness of the pipe’s inner surface. f = 64/Re
- The friction factor for turbulent flow depends strongly on the relative roughness. It is determined by the Colebrook equation. It must be noted, at very large Reynolds numbers, the friction factor is independent of the Reynolds number.
The friction factor has been determined to depend on the Reynolds number for the flow and the degree of roughness of the pipe’s inner surface (especially for turbulent flow). The friction factor of laminar flow is independent of roughness of the pipe’s inner surface.
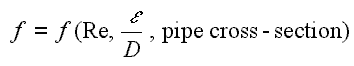
The pipe cross-section is also important, as deviations from circular cross-section will cause secondary flows that increase the head loss. Non-circular pipes and ducts are generally treated by using the hydraulic diameter.
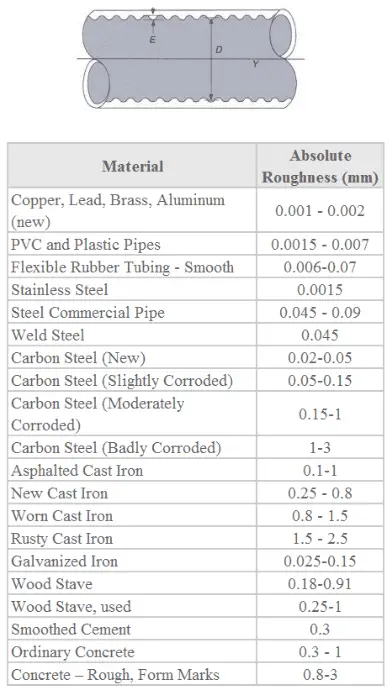
Relative Roughness
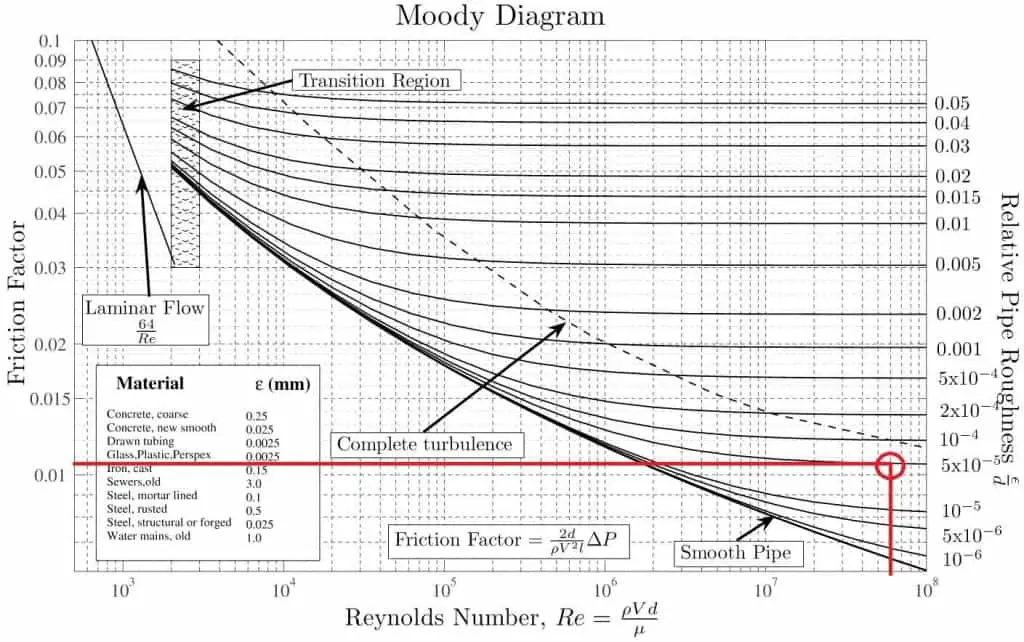
The quantity used to measure the roughness of the pipe’s inner surface is called the relative roughness, and it is equal to the average height of surface irregularities (ε) divided by the pipe diameter (D).
,where both the average height surface irregularities and the pipe diameter are in millimeters.
If we know the relative roughness of the pipe’s inner surface, then we can obtain the value of the friction factor from the Moody Chart.
The Moody chart (also known as the Moody diagram) is a graph in non-dimensional form that relates the Darcy friction factor, Reynolds number, and the relative roughness for fully developed flow in a circular pipe.
Darcy Friction Factor for various flow regime
The most common classification of flow regimes is according to the Reynolds number. The Reynolds number is a dimensionless number comprised of the physical characteristics of the flow and it determines whether the flow is laminar or turbulent. An increasing Reynolds number indicates an increasing turbulence of flow. As can be seen from the Moody chart, also Darcy friction factor is highly dependent on the flow regime (i.e. on the Reynolds number).
Examples
We hope, this article, Fanning Friction Factor, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.