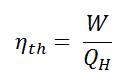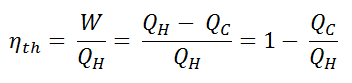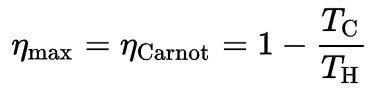Facebook Instagram Youtube Twitter

What is Example of Carnot Efficiency – Problem with Solution – Definition

by
Example of Carnot Efficiency – Problem with Solution. Calculate the carnot efficiency of coal-fired power plant. Compare it with real cycles of power plants. Thermal Engineering

Carnot Cycle – Processes

Carnot cycle - ProcessesIn a Carnot cycle, the system executing the cycle undergoes a series of four internally reversible processes: two isentropic processes (reversible adiabatic) alternated with two isothermal processes:

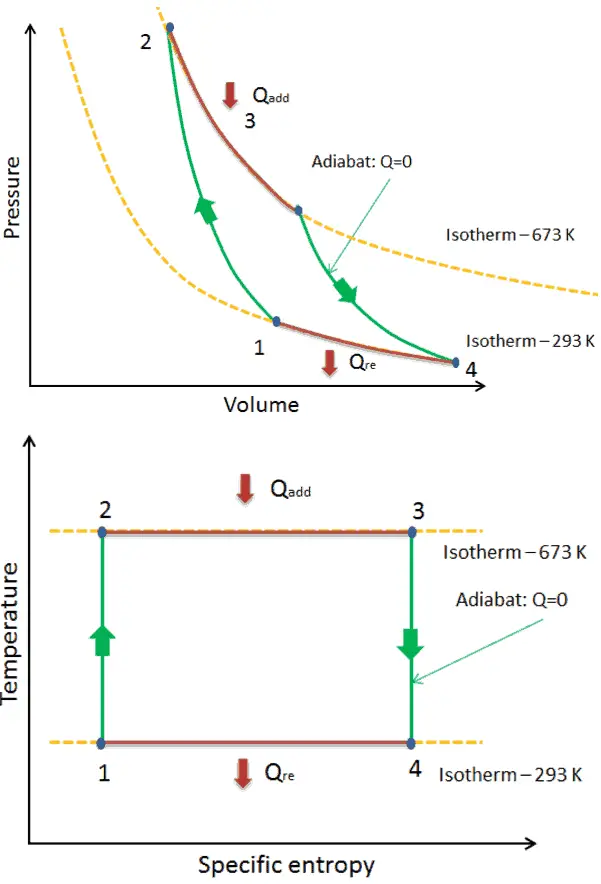
  1. isentropic compression – The gas is compressed adiabatically from state 1 to state 2, where the temperature is TH. The surroundings do work on the gas, increasing its internal energy and compressing it. On the other hand the entropy remains unchanged.
  2. Isothermal  expansion – The system is placed in contact with the reservoir at TH. The gas expands isothermally while receiving energy QH from the hot reservoir by heat transfer. The temperature of the gas does not change during the process. The gas does work on the surroundings. The total entropy change is given by: ∆S = S1 – S4 = QH/TH
  3. isentropic expansion – The gas expands adiabatically from state 3 to state 4, where the temperature is TC. The gas does work on the surroundings and loses an amount of internal energy equal to the work that leaves the system. Again the entropy remains unchanged.
  4. isothermal compression – The system is placed in contact with the reservoir at TC. The gas compresses isothermally to its initial state while it discharges energy QC to the cold reservoir by heat transfer. In this process the surroundings do work on the gas. The total entropy change is given by: ∆S = S3 – S2 = QC/TC

Carnot Cycle Efficiency

In general, the thermal efficiency, ηth, of any heat engine is defined as the ratio of the net work it does, W, to the heat input at the high temperature, QH.

thermal efficiency formula - 1

Since energy is conserved according to the first law of thermodynamics and energy cannot be be converted to work completely, the heat input, QH, must equal the work done, W, plus the heat that must be dissipated as waste heat QC into the environment. Therefore we can rewrite the formula for thermal efficiency as:

thermal efficiency formula - 2

Since QC = ∆S.TC and QH = ∆S.TH, the formula for this maximum efficiency is:

Carnot Efficiency Formula

where:

  • is the efficiency of Carnot cycle, i.e. it is the ratio = W/QH of the work done by the engine to the heat energy entering the system from the hot reservoir.
  • TC is the absolute temperature (Kelvins) of the cold reservoir,
  • TH is the absolute temperature (Kelvins) of the hot reservoir.

See also : Causes of Inefficiencies

Example: Carnot efficiency for coal-fired power plant

In a modern coal-fired power plant, the temperature of high pressure steam (Thot) would be about 400°C (673K) and Tcold, the cooling tower water temperature, would be about 20°C (293K). For this type of power plant the maximum (ideal) efficiency will be:

ηth= 1 – Tcold/Thot = 1 – 293/673 = 56%

It must be added, this is an idealized efficiency. The Carnot efficiency is valid for reversible processes. These processes cannot be achieved in real cycles of power plants. The Carnot efficiency dictates that higher efficiencies can be attained by increasing the temperature of the steam. This feature is valid also for real thermodynamic cycles. But this requires an increase in pressures inside boilers or steam generators. However, metallurgical considerations place an upper limits on such pressures. Sub-critical fossil fuel power plants, that are operated under critical pressure (i.e. lower than 22.1 MPa), can achieve 36–40% efficiency. Supercritical designs, that are operated at supercritical pressure (i.e. greater than 22.1 MPa),  have efficiencies around 43%. Most efficient and also very complex coal-fired power plants that are operated at “ultra critical” pressures (i.e. around 30 MPa) and use multiple stage reheat reach about 48% efficiency.

See also: Supercritical Reactor

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See also:

Carnot Cycle

We hope, this article, Example of Carnot Efficiency – Problem with Solution, helps you. If so, give us a like in the sidebar. Main purpose of this website is to help the public to learn some interesting and important information about thermal engineering.

Related Posts