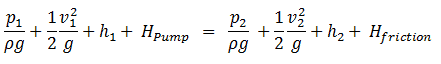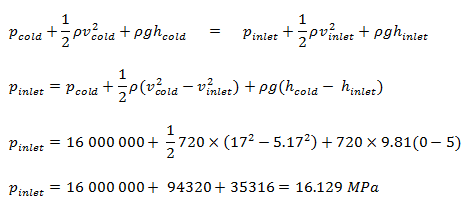Energieeinsparung
Dieses Prinzip ist allgemein als Energieeinsparungsprinzip bekannt und besagt, dass die Gesamtenergie eines isolierten Systems konstant bleibt – sie soll im Laufe der Zeit erhalten bleiben. Dies entspricht dem Ersten Hauptsatz der Thermodynamik , mit dem die allgemeine Energiegleichung in der Thermodynamik entwickelt wird. Dieses Prinzip kann bei der Analyse von fließenden Flüssigkeiten verwendet werden. Dieses Prinzip wird mathematisch durch die folgende Gleichung ausgedrückt: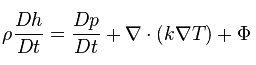 wobei h die Enthalpie ist, k die Wärmeleitfähigkeit des Fluids ist, T die Temperatur ist und Φ die viskose Dissipationsfunktion ist.
wobei h die Enthalpie ist, k die Wärmeleitfähigkeit des Fluids ist, T die Temperatur ist und Φ die viskose Dissipationsfunktion ist.
Bernoulli-Gleichung
 Die Bernoulli-Gleichung kann als Aussage über das Energieerhaltungsprinzip angesehen werden, das für fließende Flüssigkeiten geeignet ist. Es ist eine der wichtigsten / nützlichsten Gleichungen in der Strömungsmechanik . Es stellt Druck und Geschwindigkeit in einem nichtviskosen inkompressiblen Fluss in Beziehung . Die Bernoulli-Gleichung weist einige Einschränkungen in ihrer Anwendbarkeit auf, die in folgenden Punkten zusammengefasst sind:
Die Bernoulli-Gleichung kann als Aussage über das Energieerhaltungsprinzip angesehen werden, das für fließende Flüssigkeiten geeignet ist. Es ist eine der wichtigsten / nützlichsten Gleichungen in der Strömungsmechanik . Es stellt Druck und Geschwindigkeit in einem nichtviskosen inkompressiblen Fluss in Beziehung . Die Bernoulli-Gleichung weist einige Einschränkungen in ihrer Anwendbarkeit auf, die in folgenden Punkten zusammengefasst sind:
- Steady-Flow-System,
- Dichte ist konstant (was auch bedeutet, dass die Flüssigkeit inkompressibel ist),
- Es werden keine Arbeiten an oder durch die Flüssigkeit ausgeführt.
- Es wird keine Wärme auf oder von der Flüssigkeit übertragen.
- es tritt keine Änderung in der inneren Energie auf,
- Die Gleichung bezieht die Zustände an zwei Punkten entlang einer einzelnen Stromlinie (keine Bedingungen auf zwei verschiedenen Stromlinien).
Unter diesen Bedingungen wird die allgemeine Energiegleichung vereinfacht, um:
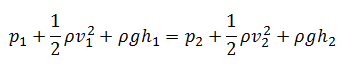
Diese Gleichung ist die bekannteste Gleichung in der Fluiddynamik . Die Bernoulli-Gleichung beschreibt das qualitative Verhalten des fließenden Fluids, das normalerweise mit dem Begriff Bernoulli-Effekt bezeichnet wird . Dieser Effekt bewirkt die Absenkung des Flüssigkeitsdrucks in Bereichen, in denen die Strömungsgeschwindigkeit erhöht wird. Diese Drucksenkung bei einer Verengung eines Strömungswegs mag kontraintuitiv erscheinen, scheint jedoch weniger intuitiv zu sein, wenn man Druck als Energiedichte betrachtet. Bei dem Hochgeschwindigkeitsfluss durch die Verengung muss die kinetische Energie auf Kosten der Druckenergie zunehmen. Die Dimensionen der Terme in der Gleichung sind kinetische Energie pro Volumeneinheit.
Erweiterte Bernoulli-Gleichung
Es gibt zwei Hauptannahmen , die bei der Ableitung der vereinfachten Bernoulli-Gleichung angewendet wurden .
- Die erste Einschränkung der Bernoulli-Gleichung besteht darin, dass keine Arbeiten an oder durch die Flüssigkeit ausgeführt werden dürfen. Dies ist eine erhebliche Einschränkung, da die meisten Hydrauliksysteme (insbesondere in der Nukleartechnik ) Pumpen enthalten. Diese Einschränkung verhindert, dass zwei Punkte in einem Flüssigkeitsstrom analysiert werden, wenn zwischen den beiden Punkten eine Pumpe vorhanden ist.
- Die zweite Einschränkung der vereinfachten Bernoulli-Gleichung besteht darin, dass bei der Lösung von Hydraulikproblemen keine Flüssigkeitsreibung zulässig ist. In der Realität spielt die Reibung eine entscheidende Rolle . Der gesamte Kopf der Flüssigkeit kann nicht vollständig und verlustfrei von einem Punkt zum anderen übertragen werden. In der Realität besteht ein Zweck von Pumpen, die in ein Hydrauliksystem eingebaut sind, darin, die Druckverluste aufgrund von Reibung zu überwinden.
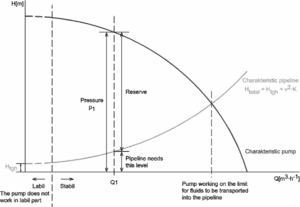
Aufgrund dieser Einschränkungen sind die meisten praktischen Anwendungen der vereinfachten Bernoulli-Gleichung auf reale Hydrauliksysteme sehr begrenzt. Um sowohl Druckverluste als auch Pumpenarbeiten zu bewältigen, muss die vereinfachte Bernoulli-Gleichung modifiziert werden .
Die Bernoulli-Gleichung kann modifiziert werden, um Gewinne und Verluste des Kopfes zu berücksichtigen . Die resultierende Gleichung, die als erweiterte Bernoulli-Gleichung bezeichnet wird , ist sehr nützlich bei der Lösung der meisten Flüssigkeitsströmungsprobleme. Die folgende Gleichung ist eine Form der erweiterten Bernoulli-Gleichung.
wobei:
h = Höhe über dem Referenzniveau (m)
v = durchschnittliche Geschwindigkeit der Flüssigkeit (m / s)
p = Druck der Flüssigkeit (Pa)
H- Pumpe = durch die Pumpe hinzugefügte Förderhöhe (m)
H- Reibung = Druckverlust aufgrund von Flüssigkeitsreibung ( m)
g = Erdbeschleunigung (m / s 2 )
Der Druckverlust (oder der Druckverlust) aufgrund von Flüssigkeitsreibung (H- Reibung ) repräsentiert die Energie, die zur Überwindung der durch die Rohrwände verursachten Reibung verwendet wird. Der in Rohren auftretende Druckverlust hängt von der Strömungsgeschwindigkeit, dem Rohrdurchmesser und der Rohrlänge sowie einem Reibungsfaktor ab, der auf der Rauheit des Rohrs und der Reynolds-Zahl der Strömung basiert . Ein Rohrleitungssystem, das viele Rohrverbindungsstücke und -verbindungen, Rohrkonvergenz, -divergenz, Windungen, Oberflächenrauheit und andere physikalische Eigenschaften enthält, erhöht auch den Druckverlust eines Hydrauliksystems.
Obwohl der Kopfverlust einen Energieverlust darstellt , stellt er keinen Verlust der Gesamtenergie der Flüssigkeit dar. Die Gesamtenergie der Flüssigkeit bleibt infolge des Energieerhaltungsgesetzes erhalten . In der Realität führt der Kopfverlust aufgrund von Reibung zu einer äquivalenten Erhöhung der inneren Energie (Temperaturerhöhung) des Fluids.
Die meisten Methoden zur Bewertung des Kopfverlusts aufgrund von Reibung basieren fast ausschließlich auf experimentellen Beweisen. Dies wird in den folgenden Abschnitten erläutert.
Beispiele – Bernoullis Prinzip
Bernoullis Effekt – Beziehung zwischen Druck und Geschwindigkeit
Es ist ein illustratives Beispiel folgende Daten nicht in jedes Reaktordesign entsprechen.

Wenn die Bernoulli-Gleichung mit der Kontinuitätsgleichung kombiniert wird, können die beiden verwendet werden, um Geschwindigkeiten und Drücke an Punkten in der Strömung zu finden, die durch eine Stromlinie verbunden sind.
Die Kontinuitätsgleichung ist einfach ein mathematischer Ausdruck des Prinzips der Massenerhaltung . Für ein Steuervolumen mit einem einzigen Einlass und einem einzigen Auslass besagt das Prinzip der Massenerhaltung, dass für einen stationären Durchfluss der Massenstrom in das Volumen gleich dem Massenstrom aus sein muss.
Beispiel:
Bestimmen Sie den Druck und die Geschwindigkeit in einem kalten Abschnitt der Primärleitung und den Druck und die Geschwindigkeit an einem Boden eines Reaktorkerns , der sich etwa 5 Meter unter dem kalten Abschnitt der Primärleitung befindet.
Nehmen wir an:
- Flüssigkeit mit konstanter Dichte ~ 720 kg / m 3 (bei 290 ° C) fließt stetig durch das kalte Bein und durch den Kernboden.
- Der primäre Rohrdurchflussquerschnitt (Einzelschleife) beträgt 0,385 m 2 (Rohrdurchmesser ~ 700 mm).
- Die Strömungsgeschwindigkeit im kalten Bein beträgt 17 m / s .
- Der Strömungsquerschnitt des Reaktorkerns beträgt 5 m 2 .
- Der Manometerdruck im kalten Bein beträgt 16 MPa .
Aufgrund des Kontinuitätsprinzips beträgt die Geschwindigkeit am Boden des Kerns:
v Einlass = v kalt . A Rohrleitung / A Kern = 17 x 1,52 / 5 = 5,17 m / s
Aufgrund des Bernoulli- Prinzips beträgt der Druck am Boden des Kerns (Kerneinlass):
Bernoullis Prinzip – Kraft heben
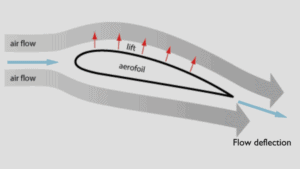
Im Allgemeinen ist der Auftrieb eine nach oben wirkende Kraft auf einen Flugzeugflügel oder ein Tragflächenprofil . Es gibt verschiedene Möglichkeiten zu erklären, wie ein Tragflügel Auftrieb erzeugt . Einige Theorien sind komplizierter oder mathematisch strenger als andere. Einige Theorien haben sich als falsch erwiesen. Es gibt Theorien, die auf dem Bernoulli-Prinzip basieren, und es gibt Theorien, die direkt auf dem dritten Newtonschen Gesetz basieren .
Die auf dem dritten Newtonschen Gesetz basierende Erklärung besagt, dass der Auftrieb durch eine Strömungsumlenkung des Luftstroms hinter dem Strömungsprofil verursacht wird. Das Schaufelblatt erzeugt Auftrieb, indem es beim Vorbeiströmen eine nach unten gerichtete Kraft auf die Luft ausübt. Nach dem dritten Newtonschen Gesetz muss die Luft eine Aufwärtskraft auf das Strömungsprofil ausüben . Dies ist eine sehr einfache Erklärung.
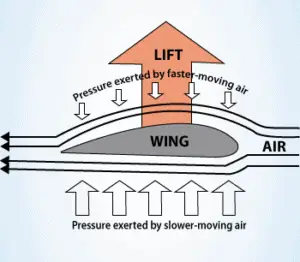
Das Bernoulli-Prinzip in Kombination mit der Kontinuitätsgleichung kann auch verwendet werden, um die Auftriebskraft auf ein Strömungsprofil zu bestimmen, wenn das Verhalten des Flüssigkeitsflusses in der Nähe der Folie bekannt ist. In dieser Erklärung ist die Form eines Tragflügels entscheidend. Die Form eines Strömungsprofils bewirkt, dass Luft oben schneller strömt als unten. Nach dem Bernoulli-Prinzip übt sich schneller bewegende Luft weniger Druck aus , und daher muss die Luft (aufgrund einer Druckdifferenz) eine Aufwärtskraft auf das Schaufelblatt ausüben .
Das Bernoulli-Prinzip erfordert, dass das Tragflächenprofil eine asymmetrische Form hat . Seine Oberfläche muss oben größer sein als unten. Wenn die Luft über das Schaufelblatt strömt, wird sie mehr von der Oberseite als von der Unterseite verdrängt. Nach dem Kontinuitätsprinzip muss diese Verschiebung zu einer Erhöhung der Strömungsgeschwindigkeit führen (was zu einer Druckabnahme führt). Die Strömungsgeschwindigkeit wird teilweise durch die untere Schaufelblattoberfläche erhöht, ist jedoch erheblich geringer als die Strömung auf der oberen Oberfläche. Die Auftriebskraft eines Tragflügels, gekennzeichnet durch den Auftriebskoeffizienten , kann während des Fluges durch Formänderungen eines Tragflügels geändert werden. Der Auftriebskoeffizient kann somit mit relativ einfachen Geräten sogar verdoppelt werden (Klappen und Lamellen ), wenn sie über die gesamte Spannweite des Flügels verwendet werden.Die Verwendung des Bernoulli-Prinzips ist möglicherweise nicht korrekt. Das Bernoulli-Prinzip geht von einer Inkompressibilität der Luft aus, aber in Wirklichkeit ist die Luft leicht komprimierbar. Es gibt jedoch weitere Einschränkungen bei Erklärungen, die auf dem Bernoulli-Prinzip beruhen. Es gibt zwei beliebte Erklärungen für den Aufzug:
- Erklärung basierend auf der Abwärtsablenkung der Strömung – Newtons drittes Gesetz
- Erklärung basierend auf Änderungen der Strömungsgeschwindigkeit und des Durchflussdrucks – Kontinuitätsprinzip und Bernoulli-Prinzip
Beide Erklärungen identifizieren einige Aspekte der Auftriebskräfte korrekt, lassen jedoch andere wichtige Aspekte des Phänomens ungeklärt. Eine umfassendere Erklärung beinhaltet sowohl Änderungen der Strömungsgeschwindigkeit als auch der Durchbiegung nach unten und erfordert eine genauere Betrachtung der Strömung.
Weitere Informationen: Doug McLean, Aerodynamik verstehen: Aus der realen Physik streiten. John Wiley & Sons Ltd. 2013. ISBN: 978-1119967514
Bernoullis Effekt – Ball in einem Luftstrom drehen
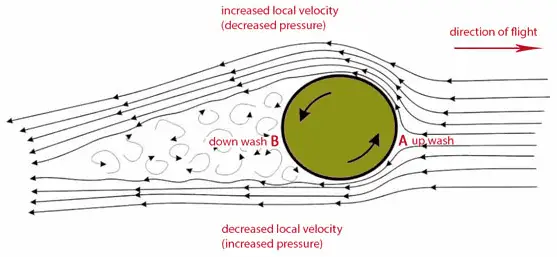 Der Bernoulli-Effekt hat eine weitere interessante interessante Konsequenz. Angenommen , ein Ball ist Spinnen , wie sie durch die Luft bewegt. Während sich der Ball dreht, zieht die Oberflächenreibung des Balls mit der Umgebungsluft eine dünne Luftschicht (als Grenzschicht bezeichnet ) mit sich. Aus dem Bild ist ersichtlich, dass sich die Grenzschicht auf einer Seite in die gleiche Richtung bewegt wie der Luftstrom, der um die Kugel fließt (oberer Pfeil), und auf der anderen Seite bewegt sich die Grenzschicht in die entgegengesetzte Richtung ( der untere Pfeil). Auf der Seite der Kugel, auf der sich der Luftstrom und die Grenzschicht in die entgegengesetzte Richtung (unterer Pfeil) bewegen, reiben sich die beidenverlangsamt den Luftstrom . Auf der gegenüberliegenden Seite bewegen sich diese Schichten in die gleiche Richtung und der Strom bewegt sich schneller .
Der Bernoulli-Effekt hat eine weitere interessante interessante Konsequenz. Angenommen , ein Ball ist Spinnen , wie sie durch die Luft bewegt. Während sich der Ball dreht, zieht die Oberflächenreibung des Balls mit der Umgebungsluft eine dünne Luftschicht (als Grenzschicht bezeichnet ) mit sich. Aus dem Bild ist ersichtlich, dass sich die Grenzschicht auf einer Seite in die gleiche Richtung bewegt wie der Luftstrom, der um die Kugel fließt (oberer Pfeil), und auf der anderen Seite bewegt sich die Grenzschicht in die entgegengesetzte Richtung ( der untere Pfeil). Auf der Seite der Kugel, auf der sich der Luftstrom und die Grenzschicht in die entgegengesetzte Richtung (unterer Pfeil) bewegen, reiben sich die beidenverlangsamt den Luftstrom . Auf der gegenüberliegenden Seite bewegen sich diese Schichten in die gleiche Richtung und der Strom bewegt sich schneller .
Nach dem Bernoulli-Prinzip übt sich schneller bewegende Luft weniger Druck aus, und daher muss die Luft eine Aufwärtskraft auf den Ball ausüben. In diesem Fall ist die Verwendung des Bernoulli-Prinzips möglicherweise nicht korrekt. Das Bernoulli-Prinzip geht von einer Inkompressibilität der Luft aus, aber in Wirklichkeit ist die Luft leicht komprimierbar. Es gibt jedoch weitere Einschränkungen bei Erklärungen, die auf dem Bernoulli-Prinzip beruhen.
Die Arbeit von Robert G. Watts und Ricardo Ferrer (Die Seitenkräfte auf eine sich drehende Kugel: Aerodynamik eines Curveballs) Dieser Effekt kann durch ein anderes Modell erklärt werden, das der sich drehenden Grenzschicht der Luft um den Ball wichtige Aufmerksamkeit widmet. Auf der Seite der Kugel, auf der sich der Luftstrom und die Grenzschicht in die entgegengesetzte Richtung bewegen (unterer Pfeil), neigt die Grenzschicht dazu, sich vorzeitig zu trennen. Auf der Seite der Kugel, auf der sich der Luftstrom und die Grenzschicht in die gleiche Richtung bewegen, trägt die Grenzschicht die Kugel weiter, bevor sie sich in eine turbulente Strömung trennt. Dies ergibt eine Strömungsumlenkungdes Luftstroms in eine Richtung hinter dem Ball. Die rotierende Kugel erzeugt Auftrieb, indem sie beim Vorbeiströmen eine nach unten gerichtete Kraft auf die Luft ausübt. Nach dem dritten Newtonschen Gesetz muss die Luft eine Aufwärtskraft auf den Ball ausüben.
Ausflussgesetz von Torricelli

Ausflussgesetz von Torricelli , auch bekannt als Torricellis Prinzip oder Torricellis Theorem , besagt in der Fluiddynamik, dass die Geschwindigkeit v von Flüssigkeit, die unter der Schwerkraft in einem Tank aus einer Öffnung fließt, proportional zur Quadratwurzel des vertikalen Abstands h ist zwischen der Flüssigkeitsoberfläche und dem Zentrum der Öffnung und zur Quadratwurzel der doppelten Beschleunigung durch die Schwerkraft (g = 9,81 N / kg nahe der Erdoberfläche).
Mit anderen Worten ist die Ausströmgeschwindigkeit des Fluids aus der Öffnung dieselbe wie die, die es durch Fallen einer Höhe h unter Schwerkraft erhalten hätte. Das Gesetz wurde 1643 von der italienischen Wissenschaftlerin Evangelista Torricelli entdeckt und nach ihr benannt. Später wurde gezeigt, dass es sich um einen besonderen Fall des Bernoulli-Prinzips handelt .
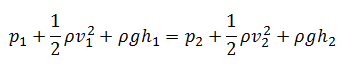
Die Torricelli-Gleichung wird für eine bestimmte Bedingung abgeleitet. Die Öffnung muss klein sein und die Viskosität und andere Verluste müssen ignoriert werden. Wenn eine Flüssigkeit durch eine sehr kleine Öffnung fließt (zum Beispiel am Boden eines großen Tanks), kann die Geschwindigkeit der Flüssigkeit am großen Ende in der Bernoulli-Gleichung vernachlässigt werden. Darüber hinaus ist die Geschwindigkeit des Ausflusses unabhängig von der Strömungsrichtung. In diesem Fall ist die Ausströmgeschwindigkeit des durch die Öffnung fließenden Fluids durch die folgende Formel gegeben:
v = √ 2gh
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.