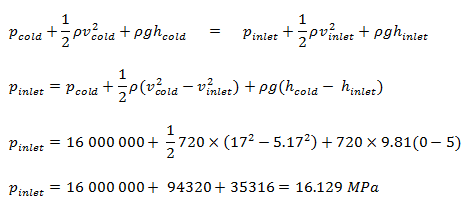Was ist Bernoullis Satz – Definition

Energieeinsparung

Dieses Prinzip ist allgemein als Energieeinsparungsprinzip bekannt und besagt, dass die Gesamtenergie eines isolierten Systems konstant bleibt – sie soll im Laufe der Zeit erhalten bleiben. Dies entspricht dem Ersten Hauptsatz der Thermodynamik , mit dem die allgemeine Energiegleichung in der Thermodynamik entwickelt wird. Dieses Prinzip kann bei der Analyse von fließenden Flüssigkeiten verwendet werden. Dieses Prinzip wird mathematisch durch die folgende Gleichung ausgedrückt: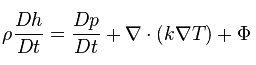wobei h die Enthalpie ist , k die Wärmeleitfähigkeit des Fluids ist, T die Temperatur ist und Φ die viskose Dissipationsfunktion ist.

Satz von Bernoulli

Der Satz von Bernoulli  kann als Aussage über das Energieerhaltungsprinzip angesehen werden, das für fließende Flüssigkeiten geeignet ist. Es ist eine der wichtigsten / nützlichsten Gleichungen in der Strömungsmechanik . Es stellt Druck und Geschwindigkeit in einem nichtviskosen inkompressiblen Fluss in Beziehung . Die Bernoulli-Gleichung weist einige Einschränkungen in ihrer Anwendbarkeit auf, die in folgenden Punkten zusammengefasst sind:

• Steady-Flow-System,
• Dichte ist konstant (was auch bedeutet, dass die Flüssigkeit inkompressibel ist),
• Es werden keine Arbeiten an oder durch die Flüssigkeit ausgeführt.
• Es wird keine Wärme auf oder von der Flüssigkeit übertragen.
• es tritt keine Änderung in der inneren Energie auf,
• Die Gleichung bezieht die Zustände an zwei Punkten entlang einer einzelnen Stromlinie (keine Bedingungen auf zwei verschiedenen Stromlinien).

Unter diesen Bedingungen wird die allgemeine Energiegleichung vereinfacht, um:

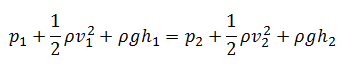
Diese Gleichung ist die bekannteste Gleichung in der Fluiddynamik . Die Bernoulli-Gleichung beschreibt das qualitative Verhalten des fließenden Fluids, das normalerweise mit dem Begriff Bernoulli-Effekt bezeichnet wird . Dieser Effekt bewirkt die Absenkung des Flüssigkeitsdrucks in Bereichen, in denen die Strömungsgeschwindigkeit erhöht wird. Diese Drucksenkung bei einer Verengung eines Strömungswegs mag kontraintuitiv erscheinen, scheint jedoch weniger intuitiv zu sein, wenn man Druck als Energiedichte betrachtet. Bei dem Hochgeschwindigkeitsfluss durch die Verengung muss die kinetische Energie auf Kosten der Druckenergie zunehmen. Die Dimensionen der Terme in der Gleichung sind kinetische Energie pro Volumeneinheit.

Bernoullis Effekt – Beziehung zwischen Druck und Geschwindigkeit

Es ist ein illustratives Beispiel folgende Daten nicht in jedes Reaktordesign entsprechen.

Wenn die Bernoulli-Gleichung mit der Kontinuitätsgleichung kombiniert wird, können die beiden verwendet werden, um Geschwindigkeiten und Drücke an Punkten in der Strömung zu finden, die durch eine Stromlinie verbunden sind.

Die Kontinuitätsgleichung ist einfach ein mathematischer Ausdruck des Prinzips der Massenerhaltung . Für ein Steuervolumen mit einem einzigen Einlass und einem einzigen Auslass besagt das Prinzip der Massenerhaltung, dass für einen stationären Durchfluss der Massenstrom in das Volumen gleich dem Massenstrom aus sein muss.

Beispiel:

Bestimmen Sie den Druck und die Geschwindigkeit in einem kalten Abschnitt der Primärleitung und den Druck und die Geschwindigkeit an einem Boden eines Reaktorkerns , der sich etwa 5 Meter unter dem kalten Abschnitt der Primärleitung befindet.

Nehmen wir an:

• Flüssigkeit mit konstanter Dichte ~ 720 kg / m ³ (bei 290 ° C) fließt stetig durch das kalte Bein und durch den Kernboden.

• Der primäre Rohrdurchflussquerschnitt (Einzelschleife) beträgt 0,385 m ² (Rohrdurchmesser ~ 700 mm).

• Die Strömungsgeschwindigkeit im kalten Bein beträgt 17 m / s .

• Der Strömungsquerschnitt des Reaktorkerns beträgt 5 m ² .

• Der Manometerdruck im kalten Bein beträgt 16 MPa .

Aufgrund des Kontinuitätsprinzips beträgt die Geschwindigkeit am Boden des Kerns:

v _Einlass = v _kalt . A _Rohrleitung / A _Kern = 17 x 1,52 / 5 = 5,17 m / s

Aufgrund des Bernoulli- Prinzips beträgt der Druck am Boden des Kerns (Kerneinlass):