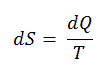Was ist Entropie – Definition

Entropieeinheiten

Die SI – Einheit für die Entropie ist J / K . Nach Clausius wurde die Entropie über die Änderung der Entropie S eines Systems definiert. Die Änderung der Entropie S, wenn ihr durch einen reversiblen Prozess bei konstanter Temperatur eine Wärmemenge Q zugesetzt wird, ist gegeben durch:

Hier ist Q die Energie, die während des Prozesses als Wärme zum oder vom System übertragen wird, und T ist die Temperatur des Systems in Kelvin während des Prozesses. Wenn wir einen reversiblen isothermen Prozess annehmen , ist die gesamte Entropieänderung gegeben durch:

∆S = S ₂ – S ₁ = Q / T.

In dieser Gleichung hängt der Quotient Q / T mit der Zunahme der Störung zusammen. Höhere Temperatur bedeutet größere Zufälligkeit der Bewegung. Bei niedrigeren Temperaturen bewirkt die Zugabe von Wärme Q eine wesentliche fraktionierte Zunahme der molekularen Bewegung und Zufälligkeit. Wenn andererseits die Substanz bereits heiß ist, trägt die gleiche Wärmemenge Q relativ wenig zur größeren molekularen Bewegung bei.

Beispiel: Entropieänderung im schmelzenden Eis

Berechnen Sie die Entropieänderung von 1 kg Eis bei 0 ° C, wenn es bei 0 ° C reversibel zu Wasser geschmolzen wird.

Da es sich um einen isothermen Prozess handelt, können wir Folgendes verwenden:

∆S = S ₂ – S ₁ = Q / T.

daher wird die Entropieänderung sein:

∆S = 334 [kJ] / 273,15 [K] = 1,22 [kJ / K]

wobei 334 Kilojoule Wärme erforderlich sind, um 1 kg Eis zu schmelzen (latente Schmelzwärme = 334 kJ / kg) und diese Wärme bei 0 ° C (273,15 K) auf das System übertragen wird.

Spezifische Entropie

Die Entropie kann durch Teilen durch die Masse zu einer intensiven oder spezifischen Variablen gemacht werden. Ingenieure verwenden die spezifische Entropie in der thermodynamischen Analyse mehr als die Entropie selbst. Die spezifische Entropie (n) eines Stoffes ist seine Entropie pro Masseneinheit. Sie entspricht der Gesamtentropie (S) geteilt durch die Gesamtmasse (m).

s = S / m

wo:

s = spezifische Entropie (J / kg)

S = Entropie (J)

m = Masse (kg)

Die Entropie quantifiziert die Energie einer Substanz, die nicht mehr für nützliche Arbeiten zur Verfügung steht. Da die Entropie so viel über die Nützlichkeit einer bei der Ausführung von Arbeiten übertragenen Wärmemenge aussagt, enthalten die Dampftabellen Werte der spezifischen Entropie (s = S / m) als Teil der tabellierten Informationen.

Im Allgemeinen ist die spezifische Entropie eine Eigenschaft einer Substanz wie Druck, Temperatur und Volumen, kann jedoch nicht direkt gemessen werden. Normalerweise wird die Entropie einer Substanz in Bezug auf einen Referenzwert angegeben. Zum Beispiel wird die spezifische Entropie von Wasser oder Dampf unter Verwendung der Referenz angegeben, dass die spezifische Entropie von Wasser bei 0,01 ° C und normalem atmosphärischem Druck Null ist , wobei s = 0,00 kJ / kg ist. Die Tatsache, dass der Absolutwert der spezifischen Entropie unbekannt ist, ist jedoch kein Problem, da bei praktischen Problemen die Änderung der spezifischen Entropie (∆s) und nicht der Absolutwert wichtig ist.

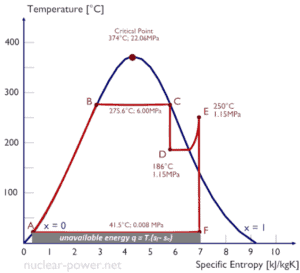
Temperatur-Entropie-Diagramme – Ts-Diagramme

Im Allgemeinen werden die Phasen eines Stoffes und die Beziehungen zwischen seinen Eigenschaften am häufigsten in Eigenschaftsdiagrammen dargestellt . Es wurde eine große Anzahl verschiedener Eigenschaften definiert, und es gibt einige Abhängigkeiten zwischen den Eigenschaften.

Ein Temperatur-Entropie-Diagramm ( Ts-Diagramm ) ist der Diagrammtyp, der am häufigsten zur Analyse von Energieübertragungssystemzyklen verwendet wird. Es wird in der Thermodynamik verwendet, um Änderungen der Temperatur und der spezifischen Entropie während eines thermodynamischen Prozesses oder Zyklus zu visualisieren.

Dies liegt daran , die Arbeit von oder auf dem System und die getan Wärme hinzugefügt oder entfernt aus dem System kann auf dem visualisiert wird Ts Diagramm . Nach der Definition der Entropie entspricht die Wärme, die zu oder von einem System übertragen wird, der Fläche unter der Ts-Kurve des Prozesses.

dQ = TdS

Ein isentropischer Prozess wird in einem Ts-Diagramm als vertikale Linie dargestellt, während ein isothermer Prozess eine horizontale Linie ist. In einem idealisierten Zustand ist die Kompression eine Pumpe, die Kompression in einem Kompressor und die Expansion in einer Turbine sind isentrope Prozesse. Daher ist es in der Energietechnik sehr nützlich, da diese Geräte in thermodynamischen Kreisläufen von Kraftwerken eingesetzt werden.

Beachten Sie, dass die isentropischen Annahmen nur für ideale Kreisprozessen gelten. Reale thermodynamische Kreisprozessen haben inhärente Energieverluste aufgrund der Ineffizienz von Kompressoren und Turbinen.

Irreversibilität natürlicher Prozesse

Nach dem zweiten Hauptsatz der Thermodynamik:

Die Entropie eines isolierten Systems nimmt niemals ab. In einem natürlichen thermodynamischen Prozess nimmt die Summe der Entropien der wechselwirkenden thermodynamischen Systeme zu.  

Dieses Gesetz gibt die Unumkehrbarkeit der natürlichen Prozesse . Reversible Prozesse sind eine nützliche und bequeme theoretische Fiktion, kommen aber in der Natur nicht vor. Aus diesem Gesetz folgt, dass es unmöglich ist, eine Vorrichtung zu konstruieren, die in einem Zyklus arbeitet und deren einzige Wirkung die Übertragung von Wärme von einem kühleren Körper auf einen heißeren Körper ist. Daraus folgt, dass Perpetual-Motion-Maschinen der zweiten Art unmöglich sind.

Entropie bei absolutem Nullpunkt

Nach dem dritten Hauptsatz der Thermodynamik:

Die Entropie eines Systems nähert sich einem konstanten Wert, wenn sich die Temperatur dem absoluten Nullpunkt nähert.

Basierend auf empirischen Beweisen besagt dieses Gesetz, dass die Entropie einer reinen kristallinen Substanz beim absoluten Nullpunkt der Temperatur 0 K Null ist und dass es mit keinem noch so idealisierten Verfahren möglich ist, die Temperatur eines Systems zu senken in einer endlichen Anzahl von Schritten auf den absoluten Nullpunkt. Dies ermöglicht es uns, einen Nullpunkt für die Wärmeenergie eines Körpers zu definieren.

Absoluter Nullpunkt ist die kälteste theoretische Temperatur, bei der die thermische Bewegung von Atomen und Molekülen ihr Minimum erreicht. Dies ist ein Zustand, in dem die Enthalpie und Entropie eines abgekühlten idealen Gases ihren Minimalwert von 0 erreicht. Klassischerweise wäre dies ein Zustand der Bewegungslosigkeit , aber die Quantenunsicherheit schreibt vor, dass die Teilchen immer noch eine endliche Nullpunktsenergie besitzen . Der absolute Nullpunkt wird auf der Kelvin-Skala als 0 K, auf der Celsius-Skala als –273,15 ° C und auf der Fahrenheit-Skala als –459,67 ° F bezeichnet .