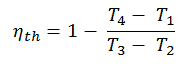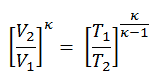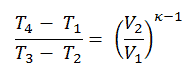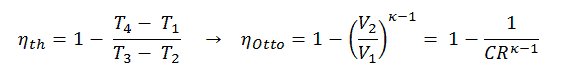Kompressionsverhältnis – Otto-Motor
Das Verdichtungsverhältnis , CR , ist als das Verhältnis des Volumens im unteren Totpunkt und das Volumen am oberen Totpunkt definiert ist . Es ist ein Schlüsselmerkmal für viele Verbrennungsmotoren. Im folgenden Abschnitt wird gezeigt, dass das Verdichtungsverhältnis den thermischen Wirkungsgrad des verwendeten thermodynamischen Zyklus des Verbrennungsmotors bestimmt. Im Allgemeinen ist ein hohes Verdichtungsverhältnis erwünscht, da ein Motor dadurch einen höheren thermischen Wirkungsgrad erreichen kann.
Es sei beispielsweise einen Otto – Zyklus mit Kompressionsverhältnis CR annehmen = 10: 1. Das Volumen der Kammer beträgt 500 cm³ = 500 × 10 -6 m 3 (0,5 l) vor dem Verdichtungstakt. Für diesen Motor eines erforderlichen ll Band sind bekannt:
- V 1 = V 4 = V max = 500 × 10 –6 m 3 (0,5 l)
- V 2 = V 3 = V min = V max / CR = 55,56 × 10 –6 m 3
Beachten Sie, dass (V max – V min ) x Anzahl der Zylinder = Gesamtmotorhubraum.
Wärmewirkungsgrad für den Otto-Zyklus
Im allgemeinen wird die thermischen Wirkungsgrad , η th , ein Wärmekraftmaschine ist als das Verhältnis der definierten Arbeits es tut, W , an den Wärmeeingang bei der hohen Temperatur, Q H .
Der thermische Wirkungsgrad , η th , stellt den Anteil an Wärme , Q H , die konvertiert wird , zu arbeiten . Da nach dem ersten Hauptsatz der Thermodynamik Energie gespart wird und Energie nicht vollständig in Arbeit umgewandelt werden kann , muss der Wärmeeintrag Q H gleich der geleisteten Arbeit W sein, zuzüglich der Wärme, die als Abwärme Q C in die Wärme abgeführt werden muss Umgebung. Daher können wir die Formel für den thermischen Wirkungsgrad wie folgt umschreiben:
Die absorbierte Wärme tritt während der Verbrennung des Kraftstoff-Luft-Gemisches auf, wenn der Funke ungefähr bei konstantem Volumen auftritt. Da während eines isochoren Prozesses keine Arbeit von oder am System ausgeführt wird, schreibt der erste Hauptsatz der Thermodynamik ∆U = ∆Q vor. Daher ist die hinzugefügte und abgegebene Wärme gegeben durch:
Q add = mc v (T 3 – T 2 )
Q out = mc v (T 4 – T 1 )
Das Ersetzen der Ausdrücke für die Wärme, die hinzugefügt und im Ausdruck für die thermische Effizienz verworfen wird, ergibt:
Wir können den obigen Ausdruck vereinfachen, indem wir die Tatsache verwenden, dass die Prozesse 1 → 2 und von 3 → 4 adiabatisch sind und für einen adiabatischen Prozess die folgende p, V, T-Formel gültig ist:
Es kann abgeleitet werden, dass:
In dieser Gleichung ist das Verhältnis V 1 / V 2 als das Kompressionsverhältnis CR bekannt . Wenn wir den Ausdruck für den thermischen Wirkungsgrad unter Verwendung des Kompressionsverhältnisses umschreiben, schließen wir, dass der thermische Wirkungsgrad des Otto-Zyklus nach Luftstandard eine Funktion des Kompressionsverhältnisses und von κ = c p / c v ist .
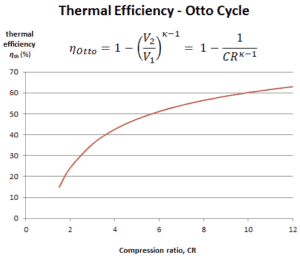
Dies ist eine sehr nützliche Schlussfolgerung, da es wünschenswert ist, ein hohes Kompressionsverhältnis zu erreichen , um mehr mechanische Energie aus einer gegebenen Masse eines Luft-Kraftstoff-Gemisches zu extrahieren. Ein höheres Verdichtungsverhältnis ermöglicht das Erreichen der gleichen Verbrennungstemperatur mit weniger Kraftstoff bei gleichzeitig längerem Expansionszyklus. Dies erzeugt mehr mechanische Leistung und senkt die Abgastemperatur . Das Absenken der Abgastemperatur bewirkt das Absenken der an die Atmosphäre abgegebenen Energie. Diese Beziehung ist in der Abbildung für κ = 1,4 dargestellt, die die Umgebungsluft darstellt.
……………………………………………………………………………………………………………………………….
Dieser Artikel basiert auf der maschinellen Übersetzung des englischen Originalartikels. Weitere Informationen finden Sie im Artikel auf Englisch. Sie können uns helfen. Wenn Sie die Übersetzung korrigieren möchten, senden Sie diese bitte an: translations@nuclear-power.com oder füllen Sie das Online-Übersetzungsformular aus. Wir bedanken uns für Ihre Hilfe und werden die Übersetzung so schnell wie möglich aktualisieren. Danke.